
- •1. Введение.
- •2. Основные определения.
- •2.1 Различимость, изоморфизм и минимизация.
- •2.2 Проблемы тестирования.
- •2.3 Установочная последовательность.
- •2.4 Синхронизирующие последовательности.
- •3. Идентификация и верификация состояния.
- •3.2. Простые условные диагностические эксперименты.
- •3.3. Построение простого условного диагностического эксперимента.
- •3.4. Верификация состояния.
- •4. Тест На Соответствие.
- •4.1. Статусные Сообщения и Сброс.
- •4.2. Разделяющие Последовательности.
- •5. Вывод.
- •6. Список литературы
- •7.Приложение.
4.2. Разделяющие Последовательности.
Для автомата с разделяющей последовательностью существует алгоритм с детерминированным полиномным алгоритмом, строящий тестовую последовательность полиномной длины. Для начала обсудим тестовый эксперимент, использующий простой безусловный диагностический эксперимент, затем условный.
Простой
диагностический эксперимент
подобна ненадежному статусному сообщению
тем, что она выдает разные выходы для
каждого состояния, но различается тем,
что она меняет состояние. Мы включаем
простой
диагностический эксперимент
 в каждый
в каждый
 для каждого состояния. Сначала проверяем,
подобен ли автомат B автомату-эталону
A тестовой последовательностью, наблюдая
за поведением каждого состояния под
действием простого
диагностического эксперимента.
Затем подтверждаем каждый переход,
проверяя конечное состояние все простой
тем же экспериментом.
для каждого состояния. Сначала проверяем,
подобен ли автомат B автомату-эталону
A тестовой последовательностью, наблюдая
за поведением каждого состояния под
действием простого
диагностического эксперимента.
Затем подтверждаем каждый переход,
проверяя конечное состояние все простой
тем же экспериментом.
Переводящая
последовательность
 это последовательность, которая переводит
автомат из состояния
это последовательность, которая переводит
автомат из состояния
 в
в
 .
Такая последовательность всегда
существует, т.к. автомат сильно связный.
Очевидно, она не единственна и выбор
кратчайшего пути является предпочтительным.
Допустим, автомат находится в состоянии
.
Такая последовательность всегда
существует, т.к. автомат сильно связный.
Очевидно, она не единственна и выбор
кратчайшего пути является предпочтительным.
Допустим, автомат находится в состоянии
 ,
тогда простой
диагностический эксперимент
,
тогда простой
диагностический эксперимент
 переводит автомат в состояние
переводит автомат в состояние
 ,
т.е.
,
т.е.
 ,
i=1,….,n.
Для автомата в начальном состоянии
,
i=1,….,n.
Для автомата в начальном состоянии
 ,
следующая тестовая последовательность
проводит автомат через каждое состояние
и показывает каждую из n реакций на
простой
диагностический эксперимент.
,
следующая тестовая последовательность
проводит автомат через каждое состояние
и показывает каждую из n реакций на
простой
диагностический эксперимент.

 (1)
(1)
Начиная
в
 ,
,
 переводит автомат в состояние
переводит автомат в состояние
 и затем
и затем
 переводит его в
переводит его в
 и выдает ответ
и выдает ответ
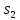 на
на
 .
В конце автомат отвечает на
.
В конце автомат отвечает на
 .
Если все работает корректно, автомат
будет в состоянии
.
Если все работает корректно, автомат
будет в состоянии
 и это проверяется простым
диагностическим экспериментом
и это проверяется простым
диагностическим экспериментом
 .
В течение теста мы увидим n реакций
автомата на последовательность
.
В течение теста мы увидим n реакций
автомата на последовательность
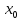 из различных n
состояний. Таким образом, мы проверяем
B на подобность автомату-эталону A.
из различных n
состояний. Таким образом, мы проверяем
B на подобность автомату-эталону A.
Затем
рассматриваем каждый переход среди
состояний. Допустим, хотим проверить
переход
 в
в
 с входом a
и выходом o,
когда автомат находится в состоянии
с входом a
и выходом o,
когда автомат находится в состоянии
 .
Сначала нужно перевести автомат из
.
Сначала нужно перевести автомат из
 в
в
 ,
подать входной символ a,
получить o,
и проверить конечное состояние
,
подать входной символ a,
получить o,
и проверить конечное состояние
 .
Мы не можем просто использовать
.
Мы не можем просто использовать
 ,
т.к. ошибки могут изменить конечное
состояние. Вместо этого, мы используем
последовательность
,
т.к. ошибки могут изменить конечное
состояние. Вместо этого, мы используем
последовательность 
 .
Сначала автомат переходит в
.
Сначала автомат переходит в , реакция которого на
, реакция которого на
 уже известна из (1).
уже известна из (1).
 .
переводит автомат в состояние
.
переводит автомат в состояние
 .
Затем проверяем правильность перехода
входным сигналом a,
затем проверяем конечное состояние
через
.
Затем проверяем правильность перехода
входным сигналом a,
затем проверяем конечное состояние
через
 .
Таким образом, следующая последовательность
проверяет корректность перехода
.
Таким образом, следующая последовательность
проверяет корректность перехода
 в
в

 .
(2)
.
(2)
После
этой последовательность автомат будет
в состоянии
 .
Повторяем этот процесс для каждого
перехода и в итоге получим проверяющую
последовательность.
.
Повторяем этот процесс для каждого
перехода и в итоге получим проверяющую
последовательность.
Пример
4. Простой безусловный диагностический
для автомата на рис.1
 =ab
и соответствующие выходы для состояний
=ab
и соответствующие выходы для состояний
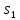 ,
, и
и
 :
01, 11 и 00, соответственно. Переводящая
последовательность, например для
:
01, 11 и 00, соответственно. Переводящая
последовательность, например для
 и
и
 :
:
 .
Последовательность из (1) для проверки
состояний есть abababab.
Затем следующая последовательность
babbab
проверяет переход
.
Последовательность из (1) для проверки
состояний есть abababab.
Затем следующая последовательность
babbab
проверяет переход
 :
b
переводит автомат в
:
b
переводит автомат в
 ,
если мы получим 01, значит ab
перевело автомат в
,
если мы получим 01, значит ab
перевело автомат в ,
наконец, bab
переводит в
,
наконец, bab
переводит в
 через b
и проверяет конечное состояние. Другие
переходы проверяются так же.
через b
и проверяет конечное состояние. Другие
переходы проверяются так же.
Мы
можем использовать простые условные
диагностические эксперименты для
постройки тестовой последовательности.
Для каждого состояния
 ,
мы рассматриваем дерево решений и берем
входную последовательность
,
мы рассматриваем дерево решений и берем
входную последовательность
 ,
идущую из корня до листа
,
идущую из корня до листа
 (см. часть III-C). Множества
(см. часть III-C). Множества
 ={
={ }
образуют разделяющее семейство. Для
примера, на рис.10 изображен простой
условный диагностический эксперимент
автомата на рис.1. Имеем,
}
образуют разделяющее семейство. Для
примера, на рис.10 изображен простой
условный диагностический эксперимент
автомата на рис.1. Имеем,
 =ab,
=ab,
 =a
и
=a
и
 =ab.
Чтобы построить тестовую последовательность,
в (1) и (2) мы заменяем
=ab.
Чтобы построить тестовую последовательность,
в (1) и (2) мы заменяем
 на каждый
на каждый
 ,
проверяющий состояние
,
проверяющий состояние
 .
Из (1) и (2) получим следующее :
.
Из (1) и (2) получим следующее :

 , где
, где
 .
.
 .
.
Простой
условный диагностический эксперимент
O( ),
а путь по всем вершинам имеет длину не
больше n, тогда последовательность в
(1) имеет длину O(
),
а путь по всем вершинам имеет длину не
больше n, тогда последовательность в
(1) имеет длину O( ).
Каждый тест из (2) имеет длину O(
).
Каждый тест из (2) имеет длину O( ),
тогда для pn переходов требуется время
O(
),
тогда для pn переходов требуется время
O(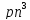 ).
Получаем тестовую последовательность
длины O(
).
Получаем тестовую последовательность
длины O( ).
Вначале построение простого условного
диагностического эксперимента занимает
время O(
).
Вначале построение простого условного
диагностического эксперимента занимает
время O( ),
и время O(pn)
для построения пути в остовном дереве
(с помощью поиска в ширину), что в итоге
требует O(
),
и время O(pn)
для построения пути в остовном дереве
(с помощью поиска в ширину), что в итоге
требует O( ).
).
Как
говорилось ранее, простые
диагностические эксперименты
схожи с ненадежным статусным сообщением,
если представим
 =
=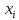
 –
эта последовательность переводит
автомат из
–
эта последовательность переводит
автомат из
 в
в
 и выдает статусное сообщение для
и выдает статусное сообщение для
 .
{
.
{ }
образуют разделяющее семейство. Тестовая
последовательность может быть получена
способом аналогичным ненадежным
статусным сообщениям через эйлеров
путь: для первого посещения состояния
}
образуют разделяющее семейство. Тестовая
последовательность может быть получена
способом аналогичным ненадежным
статусным сообщениям через эйлеров
путь: для первого посещения состояния
 применяем
применяем
 дважды, в остальных случаях по одному,
где каждый переход в
дважды, в остальных случаях по одному,
где каждый переход в
 проверяется через
проверяется через
 . Получим тестовую последовательность,
имеющую длину O(
. Получим тестовую последовательность,
имеющую длину O(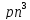 ).
).
