2.4 Синхронизирующие последовательности.

Синхронизирующая последовательность приводит автомат в одно и то же финальное состояние, вне зависимости от начального состояния и выхода. Входная последовательность x является синхронизирующей тогда и только тогда, когда

для любых пар и . То есть после подачи такой последовательности мы будем знать финальное состояние, даже не наблюдая выход. Также, каждая синхронизирующая последовательность является установочной, но не наоборот.

Конечный автомат может иметь, а может и не иметь синхронизирующую последовательность, даже если он минимизирован. За полиномиальное время можно узнать, существует ли у автомата синхронизирующая последовательность, и построить её.

Дана диаграмма переходов G автомата M, мы строим дополнительный граф GG с вершинами, по одной для каждой пары (включая пары одинаковых вершин). Существует ребро, исходящее из вершины в вершину , обозначенное входным сигналом a тогда и только тогда, когда в диаграмме G существуют переходы из в и из в , обозначенные входным сигналом a. Для автомата на рис.3 дополнительный граф изображен на рис 4. 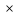Допустим сигнал a переводит состояния и в состояние , то есть в графе GG существует переход из в . Легко проверить, что существует входная последовательность, переводящая автомат из состояний и , , 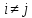в состояние тогда и только тогда, когда в графе GG существует путь из вершины в . То есть, если у автомата существует синхронизирующая последовательность, значит существует путь для всех вершин , в некоторую вершину . 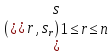Как мы покажем позже, обратное тоже верно. И существование такого пути необходимо и достаточно для существования синхронизирующей последовательности. На рис.4, в вершину 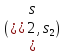можно попасть из вершин , значит автомат на рис.3 имеет синхронизирующую последовательность. Это условие достижимости может быть проверено поиском в ширину за время O(p), следовательно существование синхронизирующей последовательности может быть проверено за время O(p).

Предположим, что граф GG удовлетворяет условию достижимости. Теперь опишем алгоритм, строящий синхронизирующую последовательность за полиномиальное время. Возьмем два состояния , найдем кратчайший путь из вершины в (путь длины не больше , и обозначим этот путь как . Очевидно, . Также имеет не больше, чем n-1 состояний. Так же мы поступаем с , берем два различных состояния, находим последовательность , которая переводит их в одно состояние и получаем множество текущих состояний , состоящее из не более чем n-2 состояний. Повторяем данный процесс, пока не получим множество текущих состояний , состоящее только из одного элемента. Это всегда возможно, т.к. G удовлетворяет условию достижимости. Объединение x всех входных последовательностей переводит автомат в состояние 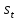, и x есть синхронизирующая последовательность. На рис.4 вершина достижима из череp сигнал a, который переводит автомат в состояние (если начинается в ) и в (если начинается в или 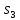). Имеем ={,}=(S,a). Так как вершина (,) достижима из (,), то ba переводит автомат в состояние , если начинается в или и имеем ={}=(,ba). Таким образом, мы получили синхронизирующую последовательность aba: (S,aba)={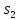} объединив сигналы a и ba.

Количество раз, когда мы объединяем пары состояний максимально равно n-1, а длина каждой объединяющей последовательности .Таким образом, длина синхронизирующей последовательности не больше . Алгоритм может быть реализован за время O(). Если на каждом шаге брать пары наиболее близкие к вершине (,), то максимальная длина синхронизирующей последовательности становится n(-1)/6. Наилучшая известная нижняя оценка .

Для данного автомата можно найти кратчайшую синхронизирующую последовательность, используя дерево решений. В этом случае нам нужно только обозначить каждую вершину дерева множеством текущих состояний, т.е. если вершина v отвечает за вход x, тогда мы обозначаем ее через (S,x). Вершина с наименьшей глубиной d, чье множество текущих состояний состоит только из одного элементоа и есть наикратчайшая синхронизирующая последовательность. Это занимает экспоненциальное время, чтобы построить дерево решений глубины d. По факту, нахождение наикратчайшей синхронизирующей последовательности есть проблема сложности-NP.