2.2 Проблемы тестирования.

В проблеме тестирования мы имеем некий автомат M, про который мы знаем некоторую информацию и хотим дополнить ее, наблюдая за вход-выходным поведением автомата. В автомат подается входная последовательность, наблюдаем выходную последовательность и получаем нужную информацию об автомате. Тест может быть безусловным (входная последовательность известная заранее) или условным (каждый следующий входной сигнал зависит от выходного поведения автомата). Простые условные диагностические эксперименты имеют более широкую область применения. Заметим что, Простой условный диагностический эксперимент это не тестовая последовательность, а дерево решений.

Мы обсудим 4 фундаментальных проблем тестирования. В первых трех имеется полное определение автомата M=(I,O,S,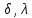), но мы не знаем его начального состояния.

Проблема I (Установочная/Синхронизирующая Последовательность): Определить финальное состояние автомата после теста.

Проблема II (Идентификация Состояния): Найти неизвестно начальное состояние.

Проблема III (Верификация Состояния): Автомат должен быть в определенном начальном состоянии, проверим, что это так.

В следующей проблеме мы тестируем автомат M, про который неизвестна его диаграмма переходов (функции переходов и выходов), а известно лишь его вход-выходное поведение и лишь небольшое количество информации, например ограничение на количество состояний.

Проблема IV (Тест На Соответствие): Дано полное определение автомата A=(I,O,S,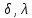) – автомат-эталон. Нужно определить эквивалентны ли M и A.

Для каждой из этих проблем главные вопросы это:

Существование: существует ли тестовая последовательность, решающая эту проблему?

Длина: При существовании такой последовательности, какова её длина?

Сложность: Как трудно определить существует ли такая последовательность, как трудно ее найти и как трудно построить кратчайшую?

Проблема I решается установочными и синхронизирующими последовательностями, и описываются они в части 2.3 и 2.4. Проблемы II и III решаются простыми диагностическими экспериментами и уникальными вход-выходными последовательностями, которые рассматриваются в части 3. Методы решения Проблемы IV представлены в части 4.

2.3 Установочная последовательность.

Чаще всего мы не знаем, в каком состоянии находится автомат, и хотим составить тест, пронаблюдать выходную последовательность и определить финальное состояние. Соответствующая входная последовательность называется установочной последовательностью.

Только в минимизированных автоматах можно найти установочную последовательность, иначе мы бы не смогли различить эквивалентные состояния никаким тестом. С другой стороны, каждый минимизированный автомат имеет установочную последовательность, и мы можем построить такую за полиномиальное время.

Заметим, что последовательность x является установочной, тогда и только тогда, когда все блоки неопределенности текущего состояния состоят только из одного элемента. В начале автомат может быть в любом состоянии, а значит состоит из одного множества-всех состояний S. Берем два любых состояния из одного блока, находим последовательность, которая разделяет их (она существует, потому что автомат минимизирован), применяем её к автомату и разбиваем блок текущего состояния минимум на два подблока, каждый из которых соответствует своему выходному сигналу. Повторяем данный процесс до тех пор, пока все блоки в 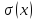не будут состоять только из одного элемента. В итоге получаем входную последовательность x, которая является установочной. 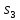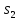Например, для автомата на рис.1 входной сигнал b отделяет от и 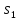, переводя автомат в состояние 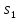, 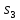и , соответственно, наблюдая выход 0. Иначе получим 1, значит автомат находится в состояни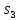и или 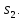Затем на вход подается сигнал a, разделяющи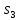й и 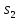выходами 0 и 1. 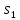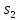Таким образом, ba - это установочная последовательность, которая переводит автомат из состояний , и 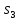в состояния 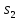, 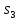и . 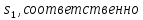Финальное состояние может быть определено наблюдая выходные последовательности 11, 10 и 00, соответственно. Заметим, что если на выход подастся b и получим 0, мы поймем, что автомат находится в состоянии 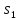и уже не нужно будет подавать a, если же получим 1 в начале, то это сделать придется. Таким образом, условный тест может быть короче, чем безусловный.

Т.к. мы можем построить разделяющую последовательность длины не больше, чем n-1 для любых двух состояний и применяем её не больше, чем n-1 раз, для того чтобы каждый блок 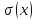состоял из одного элемента. Объединим все разделяющие последовательности и получим установочную последовательность длины не больше, чем .

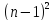Конечно, заданный автомат может иметь более короткую установочную последовательность, чем та, которую получим через описанный выше алгоритм. Легко найти кратчайшую последовательность, используя дерево решений. Нам нужно только найти вершину наименьшей длины, которая обозначена неопределенностью текущего состояния с блоками в каждом из которых, по одному элементу. Например, кратчайшая установочная последовательность для автомата на рис.1 это ba, это можно понять взглянув на его дерево решений на рис.2. Однако построение дерева решений занимает экспоненциальное время. Таким образом, поиск кратчайшей установочной последовательности это проблема сложности-NP.