3.4. Верификация состояния.

Переходим к проблеме III. Нужно проверить, что автомат M с известной диаграммой переходов находится в заданном состоянии. Это возможно тогда и только тогда, когда это состояние имеет уникальную вход-выходную последовательность (УВВ).

Определение 4. Уникальная вход-выходная последовательность x состояния s это входная последовательность x такая, что выход, получаемый автоматом с начальным состоянием s отличается от выходных последовательностей, получившихся автоматом с любым другим начальным состоянием, т.е. для любого .

Последовательность x является УВВ последовательностью состояния s тогда и только тогда, когда неопределенность начального состояния содержит s в дискретном блоке {s}. Например, для конечного автомата на рис.5, b является УВВ последовательность для , потому что он выдает 0, когда и выдают 1; состояние не имеет УВВ последовательности, а для это a.

Если автомат имеет простой безусловный или условным диагностический эксперимент, тогда все состояния имеют УВВ последовательности. Более конкретно, если дерево T это простой условный диагностический эксперимент, тогда УВВ последовательность для образуется из подписанных сигналов на пути от корня к листу, который определяет как начальное состояние. Обратное, строго говоря, неверно. С другой стороны, возможно, что ни одно состояние не имеет УВВ последовательность, что только некоторые последовательности имеют ее или что все состояния имеют УВВ последовательность, но это не гарантирует наличие простого диагностического эксперимента.

Предложенные методы нахождения УВВ последовательностей основаны на построении дерева решений, а это занимает экспоненциальное время. Таким образом эта проблема имеет PSPACE-сложность.

4. Тест На Соответствие.

Теперь обсудим Проблему IV: тест на соответствие. У нас имеется полная информация об автомате-эталоне A, известны функции переходов и выходов в виде диаграммы переходов или таблицы состояний. Также, нам дан автомат B (автомат-исполнитель) для которого известно его вход-выходное поведение. Нужно построить тест, который будет проверять, является ли B корректной реализацией A, подавая на вход B тестовую последовательность, затем рассматривая выход.

Очевидно, без каких либо дополнительных условий эта проблема нерешаема; для любой тестовой последовательности можно построить автомат B, не эквивалентный A, но на выходе ничем не отличается от A для данного теста.

Условие 1. a) Автомат A сильно связный граф, b) автомат A минимизирован,c) автомат B не изменяется во время эксперимента и имеет такой же входной алфавит, как и A, и d) автомат B имеет состояний не больше, чем A.

Автомат сильно связный, если его диаграмма переходов сильно связна, т.е. для каждой пары состояний и существует входная последовательность x такая, что

. Условие 1 a) должно выполняться, т.к. если A не будет сильно связным, эксперимент начавшийся в B в состоянии, который не может добраться до некоторых состояний не будет корректным, b) мы всегда можем минимизировать A, все равно, тестируя B, мы можем определить его с точностью до класса эквивалентных автоматов, т.к. они имеют одинаковое вход-выходное поведение, c) очевидно.

После этих объявления этих условий, мы хотим создать эксперимент, который проверяет, эквивалентен ли B с A.

Утверждение 1: Пусть A и B удовлетворяют Условию 1, тогда следующие высказывания эквивалентны:1) A и B изоморфны, 2) A и Bэквивалентны, и 3) хотя бы одно состояние A имеет эквивалентное состояние в B.

Заметим, что в описании автомата-эталона не определено начальное состояние. Если автомат содержит объявленное начальное состояние, которое нужно проверить, тогда тест может не существовать, т.к. это уже проблема верификации состояния.

С другой стороны, положим, что автомат B начинает работу из неизвестного состояния, и мы хотим проверить, изоморфен ли он A. Сначала мы подаем последовательность x, которая должна привести B к известному начальному состоянию для основной части теста, который называется тестовый эксперимент и выполняет следующее. Если B изоморфен A, тогда последовательность x приведет B в начальное состояние , потом тестовый эксперимент узнает, изоморфен ли B A. Если же B не изоморфен A, тогда последовательность x, возможно, привела, а возможно и не привела B в состояние , в обоих случая тестовый эксперимент установит неизоморфность B с A: несоответствующие выходы A и B укажут на это.

С этого момента мы полагаем, что автомат B приведен в заданное начальное состояние s.

Определение 5. Пусть A есть конечный автомат с n состояниями и начальным состоянием . Тестовая последовательность для A это входная последовательность x, которая отличает A от всех других автоматов с n состояниями, т.е. любой автомат B с максимум n состояниями, неизоморфный A, в ответ на x выдает последовательность сигналов несовпадающую с выходом A.

Для всех методов тестового эксперимента имеется основная идея. Мы хотим удостовериться в том, что каждый переход в автомате-эталоне A соответственно корректно выполняется в автомате B. Таким образом, для каждого перехода в A, скажем, из состояния в состояние , под действием сигнала a, мы хотим подать последовательность, переводящую автомат в , затем сигнал a, чтобы проверить, что финальное состояние B это 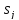, подавая на вход соответствующие входные сигналы. Методы различаются типами подпоследовательностями, которыми они проверяют нахождение автомата в определенном состоянии. Эту роль могут выполнять статусные сообщения, семейства разделяющих последовательностей, простые диагностические эксперименты, уникальные вход-выходные последовательности, характеризующие последовательности и идентифицирующие последовательности. Рассмотрим некоторые из них. Для начала, опишем основные понятия.

Семейство разделяющих последовательностей для автомата A, это набор n множеств , i=1,….n, последовательностей (одно множество для каждого состояния) таких, что для каждой пары состояний и есть последовательность x, которая разделяет их, т.е. , и 2) x является частью каких то последовательностей в и . Мы называем разделяющим множеством состояния , а элементы 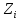разделяющими последовательностями.

Есть несколько методов выбора разделяющих множеств для конечного автомата. Если автомат A имеет простой безусловный диагностический эксперимент x, тогда можем выбрать все как x. Если A имеет простой условный диагностический эксперимент, тогда можем выбрать , состоящее из одного элемента, являющийся входной последовательностью для которой простой условный диагностический эксперимент устанавливает, что есть начальное состояние (т.е. входная последовательность, которая берет начало в корне дерева и следует до листа, обозначенного ).

Каждый минимизированный автомат имеет разделяющее семейство. И мы можем построить его следующим образом. Т.к. A минимизирован, можно найти разделяющую последовательность для любых двух состояни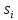й и , используя метод из II-A. Затем разбиваем состояния на блоки, в зависимости от их выходов , k=1,…,n; каждое состояние имеет x в своем множестве . Далее, для каждого блока с более чем одним состоянием, повторяем этот процесс пока каждый блок не будет состоять из одного элемента. В результате получаем семейство разделяющих последовательностей таких, что для каждой пары и соответствующие множества и содержат общую последовательность, которая их разделяет. Таких разбиений не больше, чем n-1, а каждое состоит из не более, чем n-1 последовательностей. В итоге этой процедуры получаются разными, но если мы будем включать разделяющую последовательность в , несмотря на то , чтобы входило в разбиение блока, все 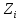получатся одинаковыми и каждый из них будет содержать по n-1 последовательностей. Такое множество последовательностей называется множеством характеризующих последовательностей; любые два состояния различимы последовательностью из этого множества. Заметим, что мы хотим, чтобы состояло из наименьшего количества последовательностей.

Мы говорим, что состояние автомата B подобно состоянию автомата A, если оно согласовано (выдает одинаковые последовательности) со всеми последовательностями из . Суть в том, что может быть подобно только одному состоянию из A. Будем говорить, что конечный автомат B подобен A, если для каждого состояния из A, B имеет подобное состояние . Заметим, что все должны быть различны, а B имеет максимум n состояний, тогда существует биективное отображение среди подобных состояний A и B.

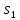Для следующих высказываний мы объявляем автомат-эталон A=(I,O,,,), а проверяемый автомат B=(I,O,,,), и полагаем, что B уже переведен в начальное состояние, которое соответствует состоянию в A.