Орловский Определенный интеграл.Практикум Част 2 2010

Рис. 9.2

Ось вращения (биссектриса первой и третьей координатных четвертей) является осью симметрии кривой. Для вычисления площади поверхности перейдем в новую систему координат поворотом на угол, равный π/4, относительно старой системы координат. Преобразование координат дается формулой:

Уравнение астроиды в новых координатах имеет вид:

Осью вращение в новой системе координат является новая ось абсцисс. График кривой в новой системе координат представлен на рис. 9.3. На этом же рисунке представлено положение старой системы координат.

191

Рис. 9.3

Астроида в новых координатах также симметрична относительно обеих координатных осей. Поэтому можно вычислить площадь поверхности вращения части кривой, отвечающей дуге ABC, и затем удвоить полученный результат. Нетрудно убедиться, что участок кривой AB отвечает значениям t [π/4; π/2], а участок BC – диапазону t [π/2; 3π/4]. По формуле (9.3)

192

193

2497. r = a(1 + cos φ) вокруг полярной оси.

График кривой (кардиоиды) представлен на рис. 9.4. Кривая симметрична относительно полярной оси (оси абс-

цисс), ее верхняя половина отвечает значениям t [0; π]. По формуле (9.4)

Учитывая тригонометрические формулы

()

194

y 6

Рис. 9.4

2498. r2 = a2 cos 2φ: а) вокруг полярной оси; б) вокруг оси φ = π/2; в) вокруг оси φ = π/4.

График рассматриваемой кривой, которая называется лемнискатой, представлен на рис. 9.5. Кривая симметрична относительно обеих координатных осей, ее график проходит в двух секторах: −π/4 6 φ 6 π/4 и 3π/4 6 φ 6 5π/4.

Рис. 9.5

а). Участок кривой, лежащий в первой четверти, отвечает значениям φ [0; π/4]. При вращении он дает поверхность, пло-

195

щадь которой составляет половину от√всей площади. Следовательно, по формуле (9.4) для r(φ) = a cos 2φ имеем:

б). Аналогично предыдущему пункту, можно ограничиться участком кривой, лежащей в первой четверти, вычислить соответствующую площадь поверхности вращения и полученный результат удвоить. Применяя формулу (9.7), находим

в). Повернем исходную систему координат на угол, равный π/4. Тогда в новой системе координат ось вращения будет совпадать с осью абсцисс. В полярных координатах это преобразование сведется к замене величины φ на φ+π/4 (величина r остается без изменений). Таким образом, если за новыми полярными координатами оставить те же обозначения r и φ, то уравнение лемнискаты принимает вид

√

r = a − sin 2φ.

196

Рис. 9.6

График кривой в новой системе координат xO˜ y˜ показан на рис. 9.6.

Участок кривой, отвечающий φ [π/2; π], дает половину

площади вращения, следовательно, по формуле (9.4) для r =

√

= a − sin 2φ получаем:

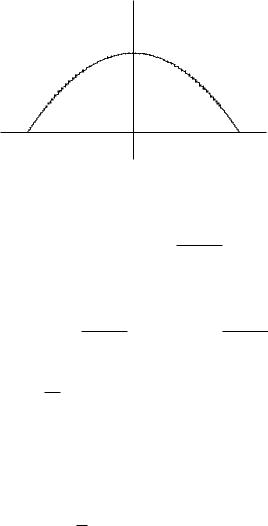
2499. Тело образовано вращением вокруг оси Ox фигуры, ограниченной параболой ay = a2 − x2 и осью Ox. Найти отношение поверхности тела вращения к поверхности равновеликого шара.

Парабола y = (a2 − x2)/a пересекает ось абсцисс в точках x = ±a (рис. 9.7).

197

6y

Рис. 9.7

Тело получается вращением криволинейной трапеции

−a 6 x 6 a, 0 6 y 6 a2 − x2 a

вокруг оси Ox. Применяя формулу (8.4) из второго раздела пре-

=2π ∫a(a4 − 2a2x2 + x4)dx = a2

198

Для нахождения площади поверхности вращения воспользуемся формулой (9.2):

Первый из полученных интегралов заменой u = 2x сводится к табличному:

Для вычисления второго интеграла сделаем ту же замену:

199

Вычислим, сначала, неопределенный интеграл