Орловский Определенный интеграл.Практикум Част 2 2010

Предисловие

Настоящая книга представляет собой учебное пособие по определенному интегралу для студентов физико-математических специальностей высших учебных заведений и университетов. За основу взят известный задачник Б. П. Демидовича [7], являющийся основным по рассматриваемой теме. Особенностью данного пособия является решение всех примеров задачника Демидовича, составляющих его четвертую главу. В связи с этим сохранена нумерация задач, принятая в [7], и поэтому первая задача в пособии имеет номер 2181. Помимо примеров из указанного выше задачника в тексте присутствуют задачи полезные для понимания дальнейшего материала. Они имеют свою нумерацию, и их решения или ответы к ним приведены в конце пособия.

Пособие состоит из двух частей. В первой части рассматриваются фундаментальные понятия, связанные с определенным интегралом. Вторая часть пособия посвящена приложениям определенного интеграла.

Впособии практически нет теоретического материала, упор делается на практическую сторону вопроса. Тем не менее теоретическая сторона предмета важна для правильного понимания предмета. Поэтому читателю рекомендуется одновременно читать и соответствующие разделы учебника. Ссылки на общепринятые учебники и пособия, аналогичные данному, приведены в списке литературы. В качестве учебников можно рекомендовать книги [2] – [5], а в качестве пособий по практическому решению задач издания [6] и [8].

Вкниге используются значения некоторых неопределенных интегралов из задачника [7]. Вычисление этих интегралов не приводится, читатель может ознакомиться с решением этих задач в [1].

Данное пособие может быть полезно не только студентам и преподавателям, но и всем тем, кто интересуется высшей математикой.

3

Глава 6

Площадь фигуры

6.1.Площадь криволинейного прямоугольника

Если фигура ограничена прямыми x = a, x = b (a < b) и графиками функций y = f(x), y = g(x) (a 6 x 6 b, f(x) > g(x)) (рис. 6.1),

a

Аналогично, если фигура ограничена прямыми y = c, y = d (c < d) и графиками функций x = φ(y), x = ψ(y) (c 6 y 6 d, φ(y) > ψ(y)) (рис. 6.2),

4

c

2396. Доказать, что площадь прямого параболического сегмента равна

S = 23 bh,

где b – основание и h – высота сегмента (рис. 6.3).

Выберем оси координат так, чтобы ось абсцисс проходила по основанию сегмента, а ось ординат проходила вдоль оси симметрии сегмента. В этом случае параболический участок границы сегмента представляет собой график функции

y = h − 4bh2 x2,

[]

5

Искомая площадь равна интегралу:

−b/2

Так как подынтегральная функция четна, то интеграл в симметричных пределах можно заменить удвоенным интегралом по неотрицательной части промежутка интегрирования:

Найти площади фигур, ограниченных кривыми, заданными в прямоугольных координатах (все параметры считаются положительными):

2397. ax = y2, ay = x2.

6

6y

Фигура ограничена прямыми x = 0, x = a и графиками функ-

√

ций y = x2/a (нижняя часть границы) и y = ax (верхняя часть границы) (рис. 6.5). Искомая площадь

2398. y = x2, x + y = 2.

Рис. 6.6

Фигура ограничена прямыми x = −2, x = 1 и графиками

7

функций y = x2 (нижняя часть границы) и y = 2 − x (верхняя часть границы) (рис. 6.6). Искомая площадь

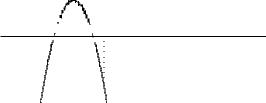
2399. y = 2x − x2, x + y = 0.

Рис. 6.7

Фигура ограничена прямыми x = 0, x = 3 и графиками функций y = −x (нижняя часть границы) и y = 2x−x2 (верхняя часть границы) (рис. 6.7). Искомая площадь

2400. y = | lg x|, y = 0, x = 0,1, x = 10.

8

q -x

1

Рис. 6.8

Разбиваем фигуру на две. Первая из них ограничена прямыми x = 0,1, x = 1 и графиками функций y = 0 (нижняя часть границы) и y = | lg x| = − lg x (верхняя часть границы). Вторая фигура ограничена прямыми x = 1, x = 10 и графиками функций y = 0 (нижняя часть границы) и y = | lg x| = lg x (верхняя часть границы) (рис. 6.8). Площадь первой фигуры

Интеграл от логарифма берем с помощью интегрирования по частям:

9

Рис. 6.9

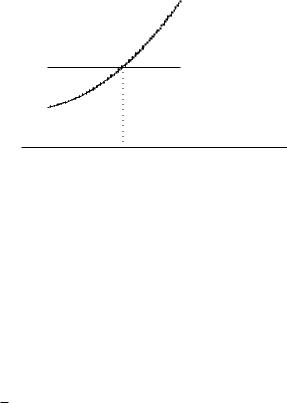
Фигура ограничена прямыми x = 0, x = 1 и графиками функций y = 2x (нижняя часть границы) и y = 2 (верхняя часть границы) (рис. 6.9). Искомая площадь

2400.2. y = (x + 1)2, x = sin πy, y = 0 (0 6 y 6 1).

Фигура ограничена прямыми y = 0, y = 1 и графиками функций x = √y −1 (левая часть границы) и x = sin πy (правая часть границы) (рис. 6.10). Искомая площадь

10