Емелянов Лекции по основам електрослабой 2007

Именно эти трансформационные свойства спиноров y и c используются для построения SUSY моделей.

Представления SUSY

В простейшем случае имеется один спинорный генератор Qa (а

также сопряженный ему генератор Qɶa ). В этом случае говорят об

N = 1 суперсимметрии. Если N > 1 , то SUSY называется расширенной.

Чтобы построить представление SUSY алгебры, которое является состоянием частицы, выберем некоторое состояние с заданной энергией Е и спиральностью l: E, λ . Подействуем на это состоя-

ние оператором Q, получим состояние с той же энергией (генератор SUSY коммутирует с Pμ ), но с другой спиральностью:

Повторное действие оператора Q даст ноль: имеется два состояния

–одно бозонное и одно фермионное (для N = 1 SUSY).

Влюбой SUSY число фермионных состояний равно числу бозонных состояний. Например:

1) пусть λ = 0 , тогда состояние l′ = ±1/ 2 содержит один комплексный скаляр и один спинор с двумя спиральными состояниями;

2) если λ = 1/ 2 , то состояние l′ = 1, 0 содержит спинорное и

векторное поля.

Минимальная суперсимметричная стандартная модель

(MSSM)

Важно отметить, что SUSY преобразования не действуют на SU(3)с, SU(2)L или U(1)Y степени свободы. Рассмотрим, например,

81

электронное поле eL. Электрон входит в SU(2)L дублет вместе с его партнером νeL:

Этот дублет требует наличия SUSY партнеров – бозонов со спином 0, образующих другой SU(2)L дублет. В СМ это хиггсовский дублет

или его зарядово-сопряженный дублет

Но эти хиггсовские дублеты не несут лептонного числа (которое будем предполагать сохраняющимся). Нельзя допускать, чтобы некоторые частицы SUSY мультиплета несли сохраняющееся квантовое число, а другие – нет. Поэтому нужны новые частицы – партнеры к дублету (4.37):

где νɶ – скалярный партнер нейтрино (снейтрино) и eɶ – скалярный партнер электрона (сэлектрон). Аналогично должны быть смюон, стау-лептон и их снейтрино. Все они принадлежат киральному супермультиплету и SU(2)L-дублетам.

Как насчет кварков? Они образуют триплет SU(3)с цветовой калибровочной группы, в стандартной модели других триплетов нет. Поэтому нужны новые скалярные партнеры кварков (скварки), являющиеся цветовыми триплетами и входящие в киральный супермультиплет.

Как обсуждалось в главе 3, электрослабые взаимодействия лептонов и кварков – « киральные», т.е. L- и R-части взаимодействуют по-разному: L-части относятся к SU(2)-дублетам, а R-части – SU(2)- синглеты. Поэтому нужны скалярные партнеры для L- и R-частей.

Например, (eR , eɶR ) , (uR ,uɶR ) , (dR , dɶR ) и т.д., а также

82

Мы пока ничего не говорили о поле SUSY со спином 1. Это поле принадлежит к векторному (или калибровочному) супермультиплету, ассоциированному с безмассовым векторным полем (с двумя степенями свободы), которое называется калибрино. У калибрино квантовые числа относительно калибровочной группы такие же, как для калибровочных бозонов. Для получения суперсимметричной КХД нужно ввести октет глюино, SU(2)L-триплет (вино и зино), а также фотино. После нарушения SU(2)L-симметрии (a la Higgs) по-

лучается три фермионных партнера W±, Z0 – соответственно Wɶ ± , Zɶ0 и фотино γɶ .

Наконец, хиггсовский сектор. Мы не может найти хиггсовскому дублету известного фермионного партнера, т.е. нужно ввести хиггсино – фермионный аналог, входящий в киральный супермультиплет. Отметим, что для построения суперсимметричной стандартной модели необходимо ввести два отдельных хиггсовский дублета:

ВSUSY моделях число бозонных степеней свободы равно числу фермионных степеней свободы. В СМ имеется 22 бозонных и 96 фермионных (с учетом правых нейтрино) степеней свободы, т.е. СМ несуперсимметрична. Для каждой частицы вводится суперпартнер. Если бы SUSY была точной, то суперпартнеры имели бы те же массы. Отсутствие SUSY объясняется тем, что их массы очень велики, т.е. SUSY должна быть нарушенной.

Втабл. 4.1 приведен состав минимальной суперсимметричной стандартной модели.

Минимальная суперсимметричная модель содержит два комплексных хиггсовских дублета, т.е. всего 8 вещественных скалярных полей. После электрослабого нарушения симметрии остается

83

пять физических хиггсовских бозонов: три нейтральных (два СРчетных h, H и один СР-нечетный А), пара заряженных бозонов Хиггса H ± . На древесном уровне хиггсовский сектор MSSM полностью определяется двумя параметрами. Обычно выбирают массу mA (СР-нечетного бозона Хиггса) и tan β – отношение вакуумных средних двух хиггсовских дублетов. Радиационные поправки сильно изменяют древесные предсказания, особенно для легчайшего СР-четного бозона Хиггса, масса которого на древесном уровне ³ mZ . Петлевые поправки чувствительны к массе t-кварка, массе скалярных частиц и смешиванию в секторе стоп-кварка. С учетом петлевых поправок, масса легкого хиггсовского бозона h ограничена сверху значением 135 ГэВ. Поэтому легкий бозон Хиггса MSSM будет нелегко отличить от бозона Хиггса СМ.

Таблица 4.1

84

Заряженные хиггсовские бозоны связаны с массой mA древес-

ным соотношением mH2 ± = mW2 + mA2 и не очень чувствительны к радиационным поправкам. Прямые поиски заряженных хиггсов в распадных модах H ± → τν и H ± ® cs на LEP дали ограничения mH ± ³ 78,6 ГэВ.

Поиск хиггсовских бозонов MSSM на LHC

Как уже отмечалось, свойства хиггсовских бозонов MSSM определяются значениями mA и tan β и радиационными поправками, а

также характером смешивания в секторе стоп-кварка. В сценарии максимального смешивания h и А практически вырождены по массе вплоть до mA » 125 ГэВ. При больших tan β усиливается связь бозонов Хиггса с b-кварком, поэтому каналом поиска является:

Основной фон – от распада Z ® m+m− . Поэтому необходима иден-

тификация b-струй.

Поиск тяжелых Н и А. При больших tan β усилена связь Н и А с фермионами down-типа. Доминирующую роль играет ассоциированное рождение хиггсовских частиц с bbH / A ® bbbb . Кроме то-

го, дает вклад процесс bbH / A ® bb tt . Для bb tt конечных состояний нужны точная идентификация b-струй и регистрация t. Для масс mA < 400 ГэВ особенно информативны процессы с одним адронным и одним лептонным распадами.

В области малых tan β тяжелые хиггсовские бозоны могут быть обнаружены по их распадам на легкие хиггсовские бозоны. Например, в модах H → hh и A → Zh .

Конечные состояния для поиска распада H → hh – моды bb gg , bb tt и bbbb . Мода bb gg могла бы быть очень привлекательной,

однако относительная вероятность распада весьма невелика.

Мода A → Zh может изучаться по конечным состояниям

85

за близости масс mA и mH разделить их по распадам на tt экспериментально невозможно.

Заряженные хиггсовские бозоны. На LHC заряженный хигг-

совский бозон может быть зарегистрирован несколькими способа-

нии с W : qq → H ±W . Предполагая, что SUSY спектр содержит

тяжелые частицы, заряженные H ± распадается только на частицы стандартной модели.

при малых tan β ).

4.2. Альтернатива SUSY: «малый хиггс» (МХ)

За год до начала работы LHC природа электрослабого нарушения симметрии остается неясной. Экспериментальные данные (LEP, ТэВатрон) свидетельствуют о том, что электрослабая симметрия нарушается одним или более хиггсовскими дублетами. Однако фундаментальные скалярные частицы испытывают радиационную нестабильность масс, и это указывает на наличие «новой физики» при энергиях порядка ТэВа.

Предположим, что электрослабые экспериментальные данные свидетельствуют о том, что никаких новых частиц вне стандартной модели (за исключением хиггсовских дублетов) с массами, меньшими электрослабого масштаба, нет. Тогда физику на электрослабом масштабе можно описать «эффективной стандартной моделью», имеющей тот же состав, что и СМ, а «новая физика» параметризуется многомерными операторами, подавленными масштабом «новой

86

физики» L ³ 1ТэВ. Многомерные операторы можно классифицировать по тем симметриям, которые они нарушают. Такими симметриями могут быть симметрии, связанные с барионным и лептонным числами (B и L), СР и симметрии ароматов. Можно экспериментальные данные, связанные с нарушением симметрий, соотнести с масштабом нарушения (табл. 4.2).

указанных выше границ?

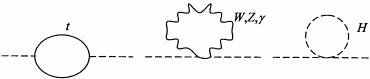
Чтобы уяснить требования на «новую физику», рассмотрим снова источник нестабильности массы бозона Хиггса. В СМ присутствуют три наиболее «опасные» радиационные поправки к массе бозона Хиггса: однопетлевые диаграммы с t-кварками, SU(2)- калибровочными бозонами и хиггсовские петли (рис. 4.2).

Рис. 4.2. Радиационные поправки к массе бозона Хиггса

Все другие диаграммы дают малые вклады, поскольку они включают малые константы связи.

Если предположить, что СМ остается справедливой вплоть до масштабов Λ~10 ТэВ, три указанные диаграммы дают вклад в

(mH )2 (табл. 4.3).

Полный квадрат массы бозона Хиггса включает сумму этих вкладов, а также квадрат массового параметра в древесном приближении. Чтобы получить значение массы бозона Хиггса на уровне электрослабого масштаба, надо выбрать масштабы обрезаний:

87

Как видно, стандартная модель с обрезанием на уровне энергий тэватрона (~1 ТэВ) весьма естественна, и не удивительно, что мы не наблюдаем новой физики.

Однако СМ с обрезанием порядка масштаба энергии LHC, уже требует точной подгонки (fine tuning), поэтому и ожидается проявление новой физики при энергиях LHC.

Можно ожидать появление новой физики, которая обрезает расходящиеся петли t-кварка на масштабе ~2 ТэВ. В слабосвязанной теории это означает, что существуют частицы с массой ~2 ТэВ. Эти частицы должны быть связаны с бозоном Хиггса, порождать новые петлевые диаграммы, сокращающие вклад t-петель. Чтобы сокращение было естественным, новые частицы должны быть связаны с t-кварком некоторой симметрией, подразумевающей, что новые частицы имеют квантовые числа, подобные t-кварку. В случае SUSY – это стоп-кварк.

Аналогично, чтобы сократить вклад петель от SU(2) калибровочных бозонов, необходимо иметь новые частицы, также связанные симметрией с калибровочными бозонами СМ. Причем сокращение будет естественным, если масса новых частиц ≤ 5 ТэВ. Наконец, расходящаяся петля бозона Хиггса требует новых частиц с массой ≤ 10 ТэВ. Сейчас известно несколько альтернатив SUSY, техницвет, дополнительные измерения и малый хиггс.

В моделях МХ считается, что бозон Хиггса – псевдо-намбу- голдстоуновский бозон (PNGB). Как будет видно, в этих теориях масса хиггсовского бозона за счет глобальных симметрий, приво-

88

дящих к сдвигу хиггсовских полей, не содержит однопетлевых квадратичных расходимостей.

Намбу-голдстоуновские бозоны (NGB)

NGB возникают при спонтанном нарушении непрерывной глобальной симметрии. Если «остаточная» симметрия точная, то NGB – строго безмассовые и имеют связи с другими частицами через производные.

Обсудим пример U(1)-симметрии.

Рассмотрим теорию с одним комплексным скалярным полем φ и

потенциалом V = V (φ*φ) , Кинетический член ∂μφ*∂μφ и потенциал

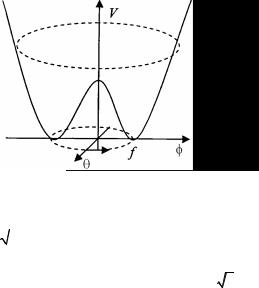
Если минимум потенциала находится не в нуле, а в точке f, как в случае потенциала «мексиканской шляпы», то U(1)-симметрия спонтанно нарушена вакуумом (рис.4.3).

Рис. 4.3. Потенциал, спонтанно нарушающий симметрию U(1)

Разложим поле возле вакуумного значения:

ходим для канонической нормировки кинетического слагаемого в лагранжиане.

89

Радиальное поле r инвариантно относительно U(1) преобразований симметрии (4.44), а поле NGB θ испытывает сдвиг:

Говорят, что U (1) симметрия нелинейно реализована.

Предположим, что мы интегрируем по массивному полю r. Мы должны быть уверены, что результирующий эффективный лагранжиан для NGB θ(x) не содержит массового члена поля θ(χ) , по-

скольку сдвиговая симметрия (4.46) подавляет все независящие от производных связи θ(χ) .

Неабелев пример NGB

Обобщая этот результат на спонтанно нарушенные неабелевы симметрии, получаем по одному NGB на каждый нарушенный генератор. Например, предположим нарушение SU (N ) → SU (N −1)

за счет вакуумного среднего поля φ. Число нарушенных генераторов в этом случае: N 2 −1 − (N −1)2 −1 = 2N −1. NGB удобно записать в виде:

причем поле π0 – вещественное, а поля π1.....πN −1 – комплексные.

Как преобразуются NGB?

Положим для простоты f = 1, тогда из (4.47) следует параметри-

90