Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

89.R. Bartholomae, D. Martin, and B. T. Sutcliffe, J. Mol. Spectrosc. 87, 367 (1981).

90.B. T. Sutcliffe, Mol. Phys. 48, 561 (1983).

91.W. H. Green, Rr., N. C. Handy, P. J. Knowles, and S. Carter, J. Chem. Phys. 94, 118 (1991).

92.M. Brommer, G. Chambaud, E.-A. Reinsch, P. Rosmus, A. Spielfiedel, N. Feautrier, and H.-J. Werner, J. Chem. Phys. 94, 8070 (1991).

93.G. Chambaud and P. Rosmus, J. Chem. Phys. 96, 77 (1992).

94.M. Brommer, P. Rosmus, S. Carter, and N. C. Handy, Mol. Phys. 77, 549 (1992).

95.M. Brommer and P. Rosmus, J. Chem. Phys. 98, 7746 (1993).

96.B. Weis and K. Yamashita. J. Chem. Phys. 99, 9512 (1993).

97.W. Gabriel, G. Chambaud, P. Rosmus, S. Carter, and N. C. Handy, Mol. Phys. 81, 1445 (1994).

98.J. Persson, B. O. Roos, and S. Carter, Mol. Phys. 84, 619 (1995).

99.G. Chambaud, P. Rosmus, M. L. Senent, and P. Palmieri, Mol. Phys. 92, 399 (1997).

100.M. Hochlaf, G. Chambaud, and P. Rosmus, J. Chem. Phys. 108, 4047 (1998).

101.D. Panten, G. Chambaud, P. Rosmus, and P. J. Knowles, Chem. Phys. Lett. 311, 390 (1994).

102.P. Jensen, M. Brumm, W. P. Kraemer, and P. R. Bunker, J. Mol. Spectrosc. 171, 31 (1995).

103.P. Jensen, M. Brumm, W. P. Kraemer, and P. R. Bunker, J. Mol. Spectrosc. 172, 194 (1995).

104.M. Kolbuszewski, P. R. Bunker, W. P. Kraemer, G. Osmann, and P. Jensen, Mol. Phys. 88, 105 (1996).

105.G. Osmann, P. R. Bunker, P. Jensen, and W. P. Kraemer, Chem. Phys. Lett. 171, 31 (1995).

106.A. Carrington, A. R. Fabris, B. J. Howard, and N. J. D. Lucas, Mol. Phys. 20, 961 (1971).

107.P. S. H. Bolman, J. M. Brown, A. Carrinngton, A. Kopp, and D. A. Ramsay, Proc. R. Soc. London, Ser. A, 343, 17 (1975).

108.J. M. Brown, J. Mol. Spectrosc. 56, 159 (1975).

109.J. M. Brown M. Kaise, C. M. L. Kerr, and D. J. Milton, Mol. Phys. 36, 553 (1978).

110.J. M. Brown and F. Jørgensen, Mol. Phys. 47, 1065 (1982).

111.P. Crozet, A. J. Ross, R. Bacis, M. P. Barnes, and J. M. Brown, J. Mol. Spectrosc. 172, 43 (1995).

112.M. Peric´, R. J. Buenker, and S. D. Peyerimhoff, Can. J. Chem. 57, 2491 (1979) .

113.P. J. Bruna, G. Hirsch, M. Peri, S. D. Peyerimhoff, and R. J. Buenker, Mol. Phys. 40, 521 (1980).

114.H. Ko¨ppel, W. Domcke, and L. S. Cederbaum, J. Chem. Phys. 74, 2945 (1980).

115.S.-K. Shih, S. D. Peyerimhoff, and R. J. Buenker, J. Mol. Spectrosc. 64, 167 (1975); 74, 124 (1979).

116.P. G. Carrick, A. J. Merer, and R. F. Curl, J. Chem. Phys. 78, 3652 (1983); R. F. Curl, P. G. Carrick, and A. J. Merer, J. Chem. Phys. 82, 3479 (1985).

117.M. Peric´, S. D. Peyerimhoff, and R. Buenker, Z. Phys. D, 24, 177 (1992).

118.H. Thu¨mmel, M. Peric´, S. D. Peyerimhoff, and R. J. Buenker, Z. Phys. D, 13, 307 (1989).

119.M. Peric´, R. Buenker, and S. D. Peyerimhoff, Mol. Phys. 71, 673 (1990).

120.M. Peric´, S. D. Peyerimhoff, and R. Buenker, Mol. Phys. 71, 693 (1990).

121.M. Peric´, S. D. Peyerimhoff, and R. Buenker, J. Mol. Spectrosc. 148, 180 (1991).

122.M. Peric´, W. Reuter, and S. D. Peyerimhoff, J. Mol. Spectrosc. 148, 201 (1991).

123.M. Peric´, B. Engels, and S. D. Peyerimhoff, J. Mol. Spetrosc. 150, 56 (1991).

124.M. Peric´, B. Engels, and S. D. Peyerimhoff, J. Mol. Spetrosc. 150, 70 (1991).

125.C. Pfelzer, M. Havenith, M. Peric´, P. Mu¨rz, and W. Urban, J. Mol. Spectrosc. 176, 28 (1996).

126.C. Schmidt, M. Peric´, P. Mu¨rz , M. Wienkoop, M. Havenith, and W. Urban, J. Mol. Spectrosc. 190, 112 (1998).

127.Y.-C. Hsu, P.-R. Wang, M.-C. Yang, D. Papousek, Y.-J. Chen, and W.-Y. Chiang, Chem. Phys. Lett. 190, 507 (1992).

128.Y.-C. Hsu, J. J.-M. Lin, D. Papousek, and Y.-J. Tsai, J. Chem. Phys. 98, 6690 (1993).

129.D. Forney, M. E. Jacox, and W. E. Thompson, J. Mol. Spectrosc. 170, 178 (1995). 32H.

130.S. Carter, N. C. Handy, C. Puzzarini, R. Tarroni, and P. Palmieri, Mol. Phys. 98, 1697 (2000).

131.G. Herzberg, Discuss. Faraday Soc. 35, 7 (1963).

132.A. N. Petelin and A. A. Kiselev, Int. J. Quantum Chem. 6, 701 (1972).

133.R. Colin, M. Herman, and I. Kopp, Mol. Phys. 37, 1397 (1979).

134.M. Takahashi, M. Fujii, and M. Ito, J. Chem. Phys. 96, 6486 (1992).

135.Y. F. Zhu, R. Shedaded, and E. R. Grant, J. Chem. Phys. 99, 5723 (1993).

136.J. E. Reutt, L. S. Wang, J. E. Pollard, D. J. Trevor, Y. T. Lee, and D. A. Shirley, J. Chem. Phys. 84, 3022 (1986).

137.S. T. Pratt, P. M. Dehmer, and J. L. Dehmer, J. Chem. Phys. 95, 6238 (1991).

138.S. T. Pratt, P. M. Dehmer, and J. L. Dehmer, J. Chem. Phys. 99, 6233 (1993).

139.J. Tang and S. Saito, J. Chem. Phys. 105, 8020 (1996).

140.M. Peric´, S. D. Peyerimhoff, and R. J. Buenker, Mol. Phys. 55, 1129 (1985).

141.M. Peric´, H. Thu¨mmel, C. M. Marian, and S. D. Peyerimhoff, J. Chem. Phys. 102, 7142 (1995).

142.M. Peric´, B. Engels, and S. D. Peyerimhoff, J. Mol. Spectrosc. 171, 494 (1995).

143.M. Peric´ and B. Engels, J. Mol. Spectrosc. 174, 334 (1995).

144.M. Peric´, B. Ostojic´, B. Scha¨fer, and B. Engels, Chem. Phys. 225, 63 (1997).

145.B. Scha¨fer, M. Peric´, and B. Engels, J. Chem. Phys. 110, 7802 (1999).

146.M. N. R. Ashfold, B. Tutcher, B. Yang, Z. K. Jin, and L. S. Anderson, J. Chem. Phys. 87, 5105 (1987).

147.M.-F. Jagod, M. Ro¨sslein, C. M. Gabrys, B. D. Rehfuss, F. Scappini, M. W. Crofton, and T. Oka, J. Chem. Phys. 97, 7111 (1992).

148.M. Peric´ and S. D. Peyerimhoff, J. Chem. Phys. 102, 3685 (1995).

149.M. Peric´, C. M. Marian, and B. Engels, Mol. Phys. 97, 731 (1966).

150.M. Peric´ and B. Ostojic´, Mol. Phys. 97, 743 (1966).

151.B. Scha¨fer-Bung, B. Engels, T. R. Taylor, D. M. Neumark, P. Botschwina, and M. Peric´, J. Chem. Phys. 115, 1777 (2001).

152.M. Peric´, C. M. Marian, and S. D. Peyerimhoff, J. Chem. Phys. 114, 6086 (1999).

153.M. Peric´, B. Ostojic´, and B. Engels, J. Chem. Phys. 105 , 8569 (1966).

154.M. Peric´ and S. D. Peyerimhoff, The Role of Rydberg States in Spectroscopy and Photochemistry, C. Sandorfy, ed., Kluwer Academic Publishers, Dordrecht/Boston/London, 1999, p. 137.

155.S. Carter and N. C. Handy, Mol. Phys. 53, 1033 (1984).

156.N. C. Handy, Mol. Phys. 61, 207 (1987).

157.M. J. Bramley, W. H. Green, Jr., and N. C. Handy, Mol. Phys. 73, 1183 (1991).

158.S. M. Colwell and N. C. Handy, Mol. Phys. 92, 317 (1997).

159.K. Sarka, J. Mol. Spectrosc. 38, 545 (1971).

160.P. R. Bunker, B. M. Landsberg, and B. P. Winnewisser, J. Mol. Spectrosc. 74, 9 (1979).

161.S. L. N. G. Krishnamachari and T. V. Venkitachalam, Chem. Phys. Lett. 55, 116 (1978).

162.S. L. N. G. Krishnamachari and D. A. Ramsay, Discuss. Faraday Soc. 71, 205 (1981).

163.B. Coquart, Can. J. Phys. 63, 1362 (1985).

164.J. M. Vrtilek, C. A. Gottlieb, E. W. Gottlieb, W. Wang, and P. Thaddeus, Astrophys. J. Lett. 398, L73 (1992).

165.P. G. Szalay, J. Chem. Phys. 105, 2735 (1996).

166.J. D. Goddard, Chem. Phys. Lett. 154, 387 (1989).

167.P. G. Szalay and J.-P. Blaudeau, J. Chem. Phys. 106, 436 (1997).

168.C. Petrongolo, J. Chem. Phys. 89, 1297 (1988).

169.A. Aguilar, M. Gonzales, and L. Poluyanov, Mol. Phys. 72, 193 (1992); 77, 209 (1992); 81, 655 (1993).

170.M. Peric´ and S. D. Peyerimhoff, J. Mol. Spectrosc. (2002), in press.

171.M. Peric´ and S. D. Peyerimhoff, J. Mol. Spectrosc. (2002), in press.

Appendix B: Antilinear Operators and Their Properties

Appendix C: Proof of Eqs. (18) and (23)

Appendix D: Degenerate and Near-Degenerate Vibrational Levels

Appendix E: Adiabatic States in the Vicinity of a Conical Intersection

I.Jahn–Teller Theorem II. Invariant Operators

III. Functional Form of the Energy Acknowledgments

References

I.INTRODUCTION

The full quantum mechanical study of nuclear dynamics in molecules has received considerable attention in recent years. An important example of such developments is the work carried out on the prototypical systems H3 [1–5] and its isotopic variant HD2 [5–8], Li3 [9–12], Na3 [13,14], and HO2 [15–18]. In particular, for the alkali metal trimers, the possibility of a conical intersection between the two lowest doublet potential energy surfaces introduces a complication that makes their theoretical study fairly challenging. Thus, alkali metal trimers have recently emerged as ideal systems to study molecular vibronic dynamics, especially the so-called geometric phase (GP) effect [13,19,20] (often referred to as the molecular Aharonov–Bohm effect [19] or Berry’s phase effect [21]); for further discussion on this topic see [22–25], and references cited therein. The same features also turn out to be present in the case of HO2, and their exact treatment assumes even further complexity [18].

For Li3, Gerber and Schumacher [9] reported the lowest vibrational levels and showed that vibronic coupling is essential to describe the electronic ground state giving rise to the so-called dynamic Jahn–Teller effect. In turn, Mayer and Cederbaum [10] studied the rovibronic coupling in the electronic A system of Li3. Most recently, Kendrick [14] reported quantum mechanical calculations on the vibrational spectrum of Na3 using a generalized Born–Oppenheimer treatment. However, a question emerges when we carry out quantum mechanical calculations using a filter diagonalization [26] technique, namely, the efficient minimal residuals (MINRES) filter diagonalization method [11,27] hereafter referred to shortly as MFD. For example, for the vibrational states of the 1H3 electronic ground state, one may compute the full spectrum of the corresponding Hamiltonian, and hence, the problem arises of whether all calculated eigenfunctions are ‘‘true’’ physical molecular vibrational states. We will provide an answer to this question in the following sections of this chapter.

Symmetry considerations have long been known to be of fundamental importance for an understanding of molecular spectra, and generally molecular dynamics [28–30]. Since electrons and nuclei have distinct statistical properties, the total molecular wave function must satisfy appropriate symmetry

requirements. Thus, not all calculated states have to be physically acceptable states, and symmetry considerations may allow us to distinguish the ‘‘mathematical states’’ from the ‘‘physical states.’’ In this chapter, we discuss the permutational symmetries of the total wave function and its various components for a molecule under the permutation of identical particles. Double group theory will be used as a powerful tool to analyze the molecular states, and an extension of Kramers’ theorem [28,30] to its most general form presented. The significant role of nuclear spin will then be emphasized, and some severe consequences will be demonstrated. Thus, the material presented here may be helpful for a detailed understanding of molecular spectra and collisional dynamics.

II.TOTAL MOLECULAR WAVE FUNCTION

The molecular time-independent nonrelativistic Schro¨dinger equation assumes the form

^ ð 0 0 Þ ¼ ð 0 0 Þ ð Þ

H R ; i; r ; s E R ; i; r ; s 1

ð 0 0 Þ ^

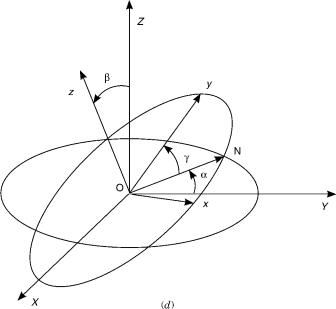
where R ; i; r ; s is the total molecular wave function, H is the total molecular Hamiltonian operator, and E is the total energy; R0 and r0 stand collectively for the nuclear and electronic coordinates in the space-fixed (SF) frame, and i and s denote the corresponding nuclear and electronic spin coordinates. For a system consisting of N nuclei and n electrons, there are 3N nuclear spacial coordinates and 3n electronic ones. In the case of a triatomic molecule, the six nuclear coordinates relative to the center of mass consist of three internal and three external coordinates. The former may be taken as the hyperspherical coordinates [2,31–35] ðr; y; fÞ, while the external or orientational coordinates are chosen to be the usual Euler angles ða; b; gÞ [36]. As illustrated in Figure 1, these define the orientation of the body-fixed (BF) relative to the SF frames. In the following

sections, we will differentiate between these two types of coordinates by

0 ¼ ð ; ^Þ ¼ ðr; y; fÞ ^ ¼ ða; b; gÞ expressing R R R , where R and R .

In the strictest meaning, the total wave function cannot be separated since there are many kinds of interactions between the nuclear and electronic degrees of freedom (see later). However, for practical purposes, one can separate the total wave function partially or completely, depending on considerations relative to the magnitude of the various interactions. Owing to the uniformity and isotropy of space, the translational and rotational degrees of freedom of an isolated molecule can be described by cyclic coordinates, and can in principle be separated. Note that the separation of the rotational degrees of freedom is not trivial [37].

where wnðR0; iÞ are the nuclear wave functions, and cnðr; s; RÞ form a complete set of electronic wave functions in BF (the summation should in principle include an integration over the continuum) obtained by solving, for each set of nuclear positions R, the following eigenequation:

As usually indicated by the semicolon, both the wave functions and eigenvalues [VnðRÞ] depend parametrically on the internal nuclear coordinates.

Substitution of Eq. (3) into the molecular Schro¨dinger equation leads to a system of coupled equations in a coupled multistate electronic manifold

where wðR0; iÞ is a column vector whose components are the nuclear wave functions wnðR0; iÞ and the matrix elements of FðR0; iÞ, GðR0; iÞ, and VðRÞ are given by

where (and hereafter) the bra–ket notation hji is used to specify integration over the electronic coordinates r and s only, and r implies taking the gradient with respect to all the nuclear degrees of freedom. Note that the nonadiabatic coupling terms [of first-order, FmnðR0; iÞ, and second-order, GmnðR0; iÞ] couple the various electronically adiabatic states, and hence are responsible for electronically nonadiabatic transitions. Note further that in the adiabatic approximation, the matrix formed by the elements Vmn ¼ Vndmn is diagonal, whereas the matrix

derived from the operator of kinetic energy of the nuclei is nondiagonal.

As is well known, perturbation theory for a single state is different from that for degenerate states. The former leads to the traditional adiabatic