
Вайнберг С. Квантовая теория полей. Том 2 (2001)
.pdf
19.5. Эффективные теории поля: пионы и нуклоны |
273 |
построенных, исходя из d = 2, m = 0 пионного взаимодействия в (19.5.33) или из d = 0, m = 1 пионного взаимодействия в (19.5.34). В этом порядке инвариантная амплитуда М, определенная выражением (19.5.24), равна
Mabcd(ν=2) = 4Fπ−2 
 δabδcd (s − m2π ) + δacδbd (t − m2π ) + δadδbc(u − m2π )
δabδcd (s − m2π ) + δacδbd (t − m2π ) + δadδbc(u − m2π ) 
 .
.
|
|
|
|
|
|
|
(19. 5. 35) |
В частности, на пороге s = 4mπ2, t = u = 0, òàê ÷òî |
|
||||||
Mabcd(ν=2) (порог) = 4m2πFπ−2 |
|
|
3δabδcd − δacδbd − δadδbc |
|
|||
|
|
||||||
= 4m2 F−2 |
|
|
7M(0) |
− 2M(2) |
|
, |
(19.5.36) |
|
|
|
|||||
π π |
|
|
ab,cd |
ab,cd |
|
|
|
ãäå Ì(0) è Ì(2) — соответствующие тензоры, представляющие двухпионные состояния с изоспином Т = 0 и Т = 2:
|
|
|
Mab(0),cd |
= |
1 |
δabδcd , |
|
|
(19.5.37) |
|
|
|
|
|
|
||||||
|
|
|
|
|
3 |
|
|
|
|
|
(2) |
|
1 F |
|
|
|
|
2 |
I |
|
|
Mab,cd |
= |
|
G |
δacδbd + δadδbc − |
|
δabδcd J , |
(19.5.38) |
|||
|
3 |
|||||||||
|
|
2 H |
|
|
|
|
K |
|
||
нормированные так, что TrM(T) = 2T + 1. Этот результат обычно записывают с помощью длин рассеяния. Согласно разделам 3.6 и 3.7, длина рассеяния aT для двух пионов в состоянии с изоспином Т равна27 произведению 1/32πmπ на коэффициент при М(Ò) â
выражении (19.5.36):
a |
|
= |
7mπ |
= 0,16m |
−1 |
, a |
|
= − |
mπ |
= −0,046m |
−1. |
0 |
|
2 |
|
||||||||
|
|
8πF2 |
π |
|
|
4πF2 |
π |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
π |
|
|
|
|
π |
|
||
Длины рассеяния пионов трудно измерять, однако тщательное изу- чение процессов типа π + N → π + π + N è K → π + π + e + ν дало следующие значения28: a0 = (0,26 ± 0,05)mπ–1, a2 = (–0,028 ± 0,012)mπ–1,
что согласуется с приведенными теоретическими значениями. Похоже, что учет поправок высших порядков по mπ/2πFπ улучшает
согласие.
Этот формализм можно распространить на описание взаимодействий пионов с нуклонами или другими частицами. Проще всего

274 |
Глава 19. Спонтанно нарушенные глобальные симметрии |
предположить, что мы добавляем слагаемое, содержащее нуклонное дублетное поле N, в тот лагранжиан, с которого мы начинали:
LN = -Nd¶/ + g[j4 + 2it × jg 5 ]iN , |
(19.5.39) |
r
r
ãäå tr — изоспиновый матричный вектор для изоспина 1/2 (т. е. паулиевский спинор tr , деленный на 2). Этот лагранжиан инвариантен относительно киральных SU(2) ´ SU(2) преобразований с
dj = 2ej4 , |
dj4 |
= -2e × j , |
(19.5.40) |
|
r |
r |
|
r r |
|
|
dN = -2ig 5e × tN . |
(19.5.41) |
||
|
|
|
r |
|
r
При устранении пионных связей без производных следует выразить нуклонное поле N как SO(4) вращение R в представлении
~
(19.5.41), действующее на новое нуклонное поле N :
|
|
|
|
|
r |
|
|
|
|
- 2ig |
r |
× z) ~ |
|
||
N º |
(1 |
5t |
|
||||
|
|
|
|
|
N , |
(19.5.42) |
|
|
|
|
|
|
|||
|
|
|
r |
||||
|
|
1 + z2 |
|
|
|||
|
|
|
|
|
|||
r
ãäå z опять дается выражением (19.5.7). После этого преобразования
~
слагаемое без производных в (19.5.39) зависит теперь только от N è s:
|
|
|
|
~ |
~ |
N[j4 |
+ 2it |
r |
|||
× jg |
5 ]N = sNN. |
||||
|
|
r |
|
|
|
С другой стороны, слагаемое с производными содержит производные от матрицы в (19.5.41), что приводит к нуклонному лагранжиану
|
|
~ L |
t ( |
r |
/ |
r |
) |
r r O |
~ |
|
||
|
|
|
|
r |
× z ´ ¶z |
|
|
|
||||
|
= - |
|
M¶/ + gs + 2i |
|
|
|
|
|
|
+ 2ig 5t × D/ PN, |
|
|
LN |
N |
|
|
|
|
|
|
(19.5.43) |
||||
|
|
|
r |
|
|
|||||||
|
|
|
NM |
|
1 + z2 |
|
|
QP |
|
|||
или в записи через канонически нормированное пионное поле (19.5.17):
|
|
~ L |
2it |
× (p ´ ¶p/ ) |
|
2ig 5t |
× ¶p/ |
|
O ~ |
|
|||
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
r |
|
|
|
LN |
= - |
N |
M¶/ + gs + |
|
|
|
+ |
|
|
|
|
PN. |
(19.5.44) |
|
r |
|
|
r |
|
|
|||||||
|
|
|
NM |
Fπ2 [1 + p2 / Fπ2 ] |
|
Fπ [1 |
+ p2 / Fπ2 |
]QP |
|
||||
Òàê êàê s имеет ненулевое вакуумное среднее, видим, что нуклон
обладает ненулевой массой, Это запрещено, если бы симметрия относительно преобразования (19.5.40), (19.5.41) была ненарушенной.


276 |
Глава 19. Спонтанно нарушенные глобальные симметрии |
|||||||||
|
|
~ |
|
D/ |
+ mN + 2igAg |
r |
r |
|
~ |
|
|
|
|
|
|
||||||
|
LN,0 = -N |
|
5t |
× D/ |
|
N, |
(19.5.48) |
|||
или в записи через пионное поле (19.5.17):
|
|
~ L |
2it |
× (p ´ ¶p/ ) |
|
2igAg 5t |
× ¶p/ |
|
O ~ |
||
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
r r |
|
|
|
r |
|
|
LN |
= - |
N |
M¶/ + mN + |
|
|
+ |
|
|
|
|
PN. (19.5.49) |
|
r |
|
r |
|
|
||||||
|
|
|
NM |
Fπ2 [1 + p2 / Fπ2 ] |
|
Fπ [1 |
+ p2 / Fπ2 |
]QP |
|||
Заметим, что мы включили произвольную константу gA в последнее слагаемое (19.5.48), так как это слагаемое само по себе кирально симметрично, и киральная симметрия не может определять коэффициент при нем. (В противоположность этому коэффициент при третьем слагаемом в (19.5.43) фиксирован условием, что это слагаемое вместе с первым образуют киральный инвариант.) Образуя дополнительное слагаемое в аксиальном токе, возникающее из нуклонного лагранжиана (19.5.48), можно проверить, что введенная здесь константа gA действительно является аксиальной константой в бета-распаде. Альтернативно, интегрируя по частям и используя уравнение Дирака, находим, что пион-нуклонное взаимодействие
~ |
|
t |
r |
~ |
|
|
|
|
-2ig Ng |
|
× (¶p/ |
)N / Fπ эквивалентно на массовой оболочке нуклона |
|||||
|
|
r |
|
|
|
|
|
|
A |
5 |
|
|
|
|
|
r |
|
|
|
|
|
~ |
|
r ~ |
, соответствующему пион- |
|
взаимодействию -4imNgANg |
5t × pN / Fπ |
|||||||
нуклонной константе связи |
|
|
||||||
GπN = 2mNgA / Fπ ,
что совпадает с соотношением Голдбергера–Треймана (19.4.33). Кстати, если бы мы использовали в этом вычислении лагран-
жиан (19.5.44), мы получили бы соотношение Голдбергера–Трейма- на с gA = 1. Однако этот результат есть на самом деле артефакт конкретного вида (19.5.39) того взаимодействия, с которого мы на- чинали. Мы могли бы включить неперенормируемое слагаемое со связью с производной *
* Левые и правые компоненты нуклонного дублета преобразуются по представлениям (1,0) и (0,1) группы SU(2) × SU(2), соответственно. Били-
нейная форма Nγ γ N является, таким образом, суммой слагаемых, квад-
μ 5 1 1
ратичных по членам ( ,0) или (0, ), т. е. она преобразуется как прямая сумма представлений (1,0), (0,0) и (0,1). В выражении (19.5.50) мы связали слагаемые (1,0) + (0,1) в Nγ μ γ 5N с антисимметричным тензором, образованным из SU(2) × SU(2) 4-векторов ϕn è ∂μϕn. Конечно, можно непосред-
ственно проверить инвариантность этого выражения относительно преобразований (19.5.40), (19.5.41).

19.5. Эффективные теории поля: пионы и нуклоны |
277 |
|
|
|
r |
|
|
|
r |
|
|
r |
|
|
|
|
L ¢ |
= ig¢N |
r |
|
- j |
|
t × ¶/ |
r |
|
r |
r |
|
|
(19.5.50) |
|
(t × j¶j/ |
4 |
4 |
× j)g |
5 |
+ t × (j ´ ¶j/ |
) |
N . |
|||||||
N |
|
|
|
|
|
|
|
|
|
|
|
|||
Непосредственно можно убедиться, что в записи через преобра- r
зованные поля s, |
~ |
è z |
это выражение принимает вид |
|||
N |
||||||
|
|
|
|
~ |
r r |
~ |
|
|
|
|
|
||
|
|
L ¢ |
= -8is2g¢N t × D/ g |
|||
|
|
5N. |
||||
|
|
N |
|
|
|
|
Поскольку s имеет ненулевое вакуумное среднее, возника-
ет вклад в пион-нуклонную константу связи и в gA, пропорциональный g¢. Отсюда значение gA = 1 не диктуется самой нарушенной SU(2) ´ SU(2) симметрией; включив взаимодействие (19.5.50) и подобрав g¢, можно придать gA любое значение.
Рассмотрим теперь, как использовать этот лагранжиан для расчета амплитуд реакций, включающих как пионы, так и нуклоны. Мы должны уделить особое внимание нуклонным пропагаторам, так как нуклон никогда не может быть «мягкой» частицей, как пион. Входящая в диаграмму нуклонная линия с 4-импульсом р порядка mN на массовой оболочке, которая затем в результате взаимодействий с мягкими пионами поглощает суммарный 4-импульс q, компоненты которого много меньше mN, будет иметь пропагатор
−i(p + q) + m |
N |
|
|
|
−ip + m |
N |
|
|
/ / |
¾¾¾® |
/ |
. |
(19.5.51) |
||||
|
|
|
|
|||||
(p + q)2 + mN2 |
q |
→ |
0 |
2p × q |
|
|
||
|
|
|
|
|||||
(Отброшенные слагаемые можно учесть, если включить в нуклонный лагранжиан слагаемые с высшими производными.) Предположим снова, что все 4-импульсы внешних пионов имеют компоненты порядка не выше Q, и определим все перенормированные констаны связи в точках перенормировки порядка Q, так что интегралы сходятся таким образом, что внутренние пионные линии также имеют 4-импульсы Q. Тогда выражение (19.5.51) показывает, что внутренние нуклонные линии дают вклад порядка 1/Q. Произвольная фейнмановская диаграмма такого процесса будет вносить вклад в инвариантную амплитуду порядка Qν, где теперь
ν = å Vi bdi + 2mi g − 2Iπ − IN + 4L. |
(19.5.52) |
i |
|
Здесь Vi — число вершин, связанных с взаимодействием типа i, di — число производных в каждом таком взаимодействии, mi —

278 |
Глава 19. Спонтанно нарушенные глобальные симметрии |
число множителей с массами кварков в каждом взаимодейстии, Iπ è IN — числа внутренних пионных и нуклонных линий, соответ-
ственно, а L — число петель в диаграмме. Используем знакомые топологические соотношения для связных диаграмм:
L = Iπ + IN − å Vi + 1 |
(19.5.53) |
i |
|
è |
|
2IN + EN = å Vini , |
(19.5.54) |
i |
|
ãäå ni — число нуклонных полей во взаимодействии типа i, а ЕN — число внешних нуклонных линий. После исключения IN è Iπ получа-
åì
|
F |
|
|
ni |
I |
|
|
|
n = å Vi G di |
+ 2mi |
+ |
|
- 2J |
+ 2L - EN |
+ 2 . |
(19.5.55) |
|
|
||||||||
i |
H |
|
|
2 |
K |
|
|
|
Здесь важно отметить, что коэффициент di + 2mi + 1ni – 2 |
в первом |
|||||||
слагаемом всегда положителен или равен нулю. Мы видели ранее, что для чисто пионных взаимодействий с ni = 0 сумма di + 2mi ³ 2, а изучение выражения (19.5.49) показывает, что для пион-нуклонных взаимодействий с ni = 2 è mi = 0 величина di ³ 1. Ясно, что всякое взаимодействие с ni = 2 è mi ³ 1 èëè ni ³ 4 имеет di ³ 2. Отсюда при Q n 2pFπ старшими являются вклады древесных
диаграмм (у которых L = 0), для которых все взаимодействия имеют
di + 2mi + ni - 2 = 0 2
Взаимодействия, удовлетворяющие этому условию, — как раз те, которые явно выписаны в лагранжианах (19.5.23), (19.5.34) и (19.5.49), плюс возможные взаимодействия с di = 0 è ni = 4
|
|
|
|
|
|
|
eNGαNjeNG |
Nj , |
(19.5.56) |
||||
~ ~ ~ |
|
α ~ |
|
|||
ãäå Ga è Ga — любые матрицы в спиновом и изоспиновом простран-
стве, которые приводят к четырехфермионным взаимодействиям, инвариантным относительно преобразований Лоренца, пространственной инверсии и изотопического спина. Эти последние взаимодействия важны для многонуклонных процессов29, которые мы здесь рассматривать не будем.


280 |
Глава 19. Спонтанно нарушенные глобальные симметрии |
где u —дираковский спинор, нормированный условием`uu = 1. Напротив, диаграмма на рис. 19.3, в дает вклад в М порядка mπ. Эту амплитуду можно записать как 2 ´ 2 матрицу по нуклонным
изоспиновым индексам:
M |
|
= |
−2i |
t |
e |
|
|
(-iq - iq¢)u , |
|
ba |
abc |
u |
|||||||
|
|||||||||
|
|
Fπ2 |
c |
|
/ / |
||||
|
|
|
|
|
|
|
|
||
ãäå q¢ и q — конечный и начальный 4-импульсы пионов, b и a —
соответствующие изовекторные индексы. Используя (19.5.57) и урав-
í |
|
å |
|
|
|
|
- |
ние Дирака в импульсном представлении ibp/ |
+ mN gu = 0, получаем |
||||||
|
−4imπ |
|
−4mπ r |
r |
|
|
|
Mba = |
|
tceabc = |
|
t × [t(π) ]ba , |
(19. 5. 58) |
||
F2 |
F2 |
||||||
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
r |
r |
ãäå [tc(π) ]ba º -iebac — пионная изовекторная матрица. Матрица t |
× t (π) |
||||||
имеет в1состояниях с полнымH изоспином Т собственные значения, равные1 [Ò(Ò +G 1) – 2 – ], так что в двух изоспиновых состояниях с Т = и Т = инвариантные амплитуды равны 30
M1/2 = 4mπ  Fπ2 , M3/2 = -2mπ
Fπ2 , M3/2 = -2mπ 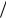 Fπ2 .
Fπ2 .
Обычно эти результаты выражаются через длины рассеяния, которые определяются как инвариантные амплитуды, деленные на
4π(1 + mπ 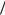 mN):
mN):
a |
|
= |
|
|
|
mπ |
|
= 0,15mπ−1, |
(19.5.59) |
|
|
|
pFπ2 |
(1 |
+ mπ mN ) |
||||||
1/2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
a3/2 |
= - |
|
|
|
mπ |
= -0,075mπ−1. |
(19.5.60) |
|||
|
|
|
|
|
||||||
2pFπ2 (1 |
+ mπ mN ) |
|||||||||
|
|
|
|
|||||||
Эти выражения находятся в разумном согласии с экспериментальными значениями12 a1/2 =(0,173 ± 0,003)mπ–1 è a3/2 = (–0,101 ± 0,004)mπ–1. (Предполагается, что результаты (19.5.59) и (19.5.60)
должны быть справедливы только в низшем порядке по отношению mπ/mN, но мы удерживаем множитель 1 + mπ/mN, òàê êàê îí
возникает просто от определения длин рассеяния.)
Поправки к длинам рассеяния следующего порядка по mπ
возникают из разных источников. Прежде всего, это диаграммы

19.5. Эффективные теории поля: пионы и нуклоны |
281 |
борновского приближения рис. 19.3, а, б, которые номинально старшего порядка, но, как мы видели, подавлены на пороге дополнительным множителем mπ/mN. Есть дополнительные древес-
ные диаграммы, содержащие вершину с двумя производными. Особый интерес представляют древесные диаграммы, содержащие вершины без производных, которые возникают от нарушающего симметрию взаимодействия, пропорционального mπ2. Ñâîé-
ства киральных и пространственно-временных преобразований этих взаимодействий должны совпадать со свойствами операторов в (19.4.34), которые являются четвертой и третьей компонетами двух различных киральных 4-векторов Fn+ è Fn–. Åñòü äâà
очевидных кандидата в такие операторы, являющеся билинейными формами по нуклонным полям: F4+-слагаемое
|
|
|
|
|
|
F 1 - z2 I |
~ ~ |
|
|
|
F |
z |
|
|
I ~ |
r ~ |
|
|||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J NN - 4iG |
|
|
|
J × Ng 5tN |
|
||||||||||||||||
NN = G |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
r |
2 |
|
r |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
H 1 |
+ z |
|
|
K |
|
|
|
|
|
|
|
H 1 + z |
|
K |
|
|
|
|
|
|
|
|||||
è F3–-слагаемое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
~ |
F z3 |
|
I |
|
r |
|
r ~ |
|
|
F z3 |
|
I |
|
~ |
||||||||||||||
|
|
~ |
~ |
|
|
|
~ |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
Nt3N = Nt3N - 2G |
|
|
|
|
J Nt |
× zN |
- iG |
|
|
|
|
J Ng |
5N. |
|||||||||||||||||||
|
|
r |
2 |
|
|
r |
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
H 1 |
+ z |
|
K |
|
|
|
|
H 1 |
+ z |
|
K |
|
||||||||||||
Киральные симметрии действуют на |
~ |
как обычные изоспиновые |
||||||||||||||||||||||||||||||
N |
||||||||||||||||||||||||||||||||
вращения, так что они не могут смешивать скалярные и псевдоскалярные нуклонные билинейные формы. Следовательно реально су-
ществуют два независимых F |
+ оператора |
|
||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
||
|
F 1 - zr |
2 I |
|
|
~ |
|
||||||
~ |
|
|||||||||||
|
G |
|
|
|
|
|
|
J NN |
(19.5.61) |
|||
|
|
|
r |
2 |
||||||||
|
H 1 |
+ z |
|
K |
|
|
|
|
||||
è |
|
|
z |
|
|
I |
|
|
|
|
||
F |
|
|
|
~ r ~ |
|
|||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
iG |
|
|
|
|
|
J × Ng 5tN |
(19.5.62) |
|||||
|
|
|
r |
2 |
||||||||
H 1 |
+ z |
|
K |
|
|
|
|
|||||
и два независимых F4– оператора

282 |
Глава 19. Спонтанно нарушенные глобальные симметрии |
|||||||||||||||
|
|
|
~ |
|
F |
|
z3 |
I |
|
r |
r ~ |
|
||||
|
~ |
|
~ |
|
||||||||||||
|
Nt3N - 2G |
|
|
|
|
|
|
J Nt |
× zN |
(19.5.63) |
||||||
|
|
|
|
r2 |
||||||||||||
|
|
|
|
|
H 1 |
+ z |
K |
|
|
|||||||
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
z3 |
|
|
I |
|
|
~ |
|
|
||||
|
|
|
|
|
~ |
|
|
|||||||||
|
|
|
iG |
|
|
|
|
J Ng 5N. |
|
(19.5.64) |
||||||
|
|
|
|
|
r |
2 |
|
|||||||||
|
|
|
H 1 |
+ z |
|
|
K |
|
|
|
|
|
||||
В следующем разделе мы покажем, что это единственные операторы со свойствами преобразований слагаемых в (19.4.34), которые билинейны по нуклонным полям. Операторы (19.5.62) и (19.5.64) оче- видно обеспечивают сохраняющие и нарушающие изоспин поправки к формуле Голдбергера–Треймана для пион-нуклонной константы связи. Два других оператора (19.5.61) и (19.5.63) непосредственно дают вклад как в массу нуклона, так и в пион-нуклонное рассеяние при низких энергиях. Из их вкладов в массу нуклона мы видим, что
эти последние слагаемые входят в эффективный лагранжиан в форме r
(с заменой z на стандартно нормированное пионное поле):
|
dmp |
+ dmn F 1 |
- p2 |
Fπ2 I ~ ~ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dLýôô = - |
|
|
G |
|
|
|
|
|
|
|
J NN |
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
r 2 |
2 |
|
|
|
|
|
|
|
||||||||
|
|
H 1 |
+ p |
Fπ |
|
K |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
L |
|
~ |
|
|
2 |
F |
p3 |
|
I |
|
r |
r ~ O |
(19.5.65) |
|||||
|
|
|
~ |
|
|
|
~ |
||||||||||||||
- (dmp |
- dmn )MNt3N - |
|
|
G |
|
|
|
|
J Nt |
× pNP |
, |
||||||||||
|
2 |
|
r |
2 |
2 |
||||||||||||||||
|
|
|
M |
|
|
|
Fπ |
H 1 |
+ p |
|
Fπ |
K |
|
|
P |
|
|||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
||
ãäå dmp è dmn — вклады слагаемых с кварковыми массами (19.4.34)
в массы протона и нейтрона. Это дает вклад в амплитуду пионнуклонного рассеяния (снова записанную как матрица в изоспиновом пространстве нуклона)
dM |
|
= |
2[δmp + δmn ] |
d |
|
+ |
2[δmp − δmn ] |
(t d |
|
+ t d |
|
) . |
(19.5.66) |
ba |
|
ab |
|
3b |
3a |
||||||||
|
|
Fπ2 |
|
Fπ2 |
a |
b |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Первое слагаемое в (19.5.65) часто называют «s-членом». Второе слагаемое — нарушающая изоспин поправка к s-члену, прояв-
ляющаяся только в процессах с участием нейтральных пионов типапроцессов с перезарядкой p+ + n → p0 + p è p– + p ® p0 + n. Õîòÿ

 m
m