Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Яско_ Диф.уравнения_Ряды

.pdf

Скачиваний:

109

Добавлен:

18.05.2015

Размер:

3.54 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 2930 / 3330 31 32 33 > Следующая >>>

Вариант 6

1.Разложить в ряд Маклорена функцию f(x), указать область сходимо-

сти	f ( x) =	2	.
		1 − 3x2

∞	2n ,		<	1
Ответ: 2 ∑ 3n x		x			.


			3
n=0			3

2.Вычислить указанную величину приближенно с заданной точностью

δ, используя разложение в степенной ряд соответствующим образом по-

добранной функции. ln 3, δ = 0,0001.

Ответ: 1,0986. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

0,5 ( + 3 )

∫ ln 1 x dx .

Ответ: 0,015. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения). y′ = x + x2 + y2 , y (0) = 1.

Ответ: y = 1 + x + 3 x2 + ...

5. Методом последовательного дифференцирования найти первые k членов разложения в степенной ряд решения дифференциального уравне- ния при указанных начальных условиях.

′	= 2x − 0,1y	2	, y (0) = 1 , k = 3.
y

Ответ: y = 1 − 0,1x + 1,01x2 + ...

6.Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию

f(х), заданную на отрезке [−π; π] .

f ( x) = 2x + 3, −π ≤ x < 0,

0 < x ≤ π.

f ( x) = 3 − π + 4 ∑ cos((2k −1) x)

π − 3) ∑ sin

((2k −1) x)

Ответ:

− ∑ sin (2kx) .

∞

k =1

(2k −1)2

k =1

2k −1

k =1 k

291

Вариант 7

1.	Разложить в ряд Маклорена функцию f(x), указать область сходимо-
сти	f ( x) = e3x .
	∞	n	n
	Ответ: ∑	3 x		,	x	< ∞ .
		3 x
		n!
2.	n=0
	n=0
	Вычислить указанную величину приближенно с заданной точностью

δ, используя разложение в степенной ряд соответствующим образом по- добранной функции. ch 2, δ = 0,0001.

Ответ: 3,7622. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

∫ x2 sin x dx .

Ответ: 0,223. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = 2cos x − xy2 , y (0) = 1.

Ответ: y = 1 + 2x − 1 x2 + ...


y′′′ = y′′ + y′2 + y3 + x , y (0) = 1 , y′(0) = 2 ,		y′′(0) = 0,5 ,					k = 6.
Ответ: y = 1 + 2x +	x2	+	11	x3 +	29	x4 +		25	x5 + ...

4		12		48			48

6.Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию

f(х), заданную на отрезке

[−π; π] .

f ( x) = 0,

−π ≤ x < 0,

3 − x,

0 ≤ x ≤ π.

f ( x) = 6 − π + 2 ∑ cos((2k −1) x) + 6 − π ∑ sin

((2k −1) x)

Ответ:

+ ∑ sin (2kx) .

∞

k =1

(2k −1)2

k =1

2k −1

k =1 2k

292

Вариант 8

1.Разложить в ряд Маклорена функцию f(x), указать область сходимо-

сти f ( x) =	1	.

1	+ x

∞

Ответ: ∑ (−1)n xn , x < 1.

n=0

2. Вычислить указанную величину приближенно с заданной точностью δ, используя разложение в степенной ряд соответствующим образом по- добранной функции. lg e, δ = 0,0001.

Ответ: 0,4343. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

1− x2

∫e 2 dx .

Ответ: 0,855. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = ex − y2 , y (0) = 0 .

Ответ: y = x + 1 x2 − 1 x3 + ...

2 6

′	= x	2	− xy , y (0) = 0,1, k = 3.
y	= x		− xy , y (0) = 0,1, k = 3.
			Ответ: y =	1	−	1	x2 +	1	x3 + ...
			Ответ: y =		−		x2 +		x3 + ...
			10		20		3

6.Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию

f(х), заданную на отрезке

[−π; π] .

f ( x) = x − 2, −π ≤ x ≤ 0,

0 < x ≤ π.

Ответ:

∞

4 + π

∞

((2k −1) x)

∞

sin (2kx)

f ( x) = − π + 4

∑

cos((2k −1) x)

∑

sin

− ∑

2k −1

π k =1

(2k −1)2

k =1

293

Вариант 9

1. Разложить в ряд Маклорена функцию f(x), указать область сходимо-

сти f ( x) = ch (2x3 ).

∞	2	n	x	6n
Ответ: ∑					,	x	< ∞ .


n=0		n!

2. Вычислить указанную величину приближенно с заданной точностью δ, используя разложение в степенной ряд соответствующим образом по- добранной функции. π, δ = 0,00001.

Ответ: 3,14159. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

0,5

∫ 1 + x2 dx .

Ответ: 0,480. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = x + y + y2 , y (0) = 1.

Ответ: y = 1 + 2x + 7 x2 + ...

5. Методом последовательного дифференцирования найти первые k членов разложения в степенной ряд решения дифференциального уравне-

ния при указанных начальных условиях.

y′′ = 2 yy′ , y (0) = 0 , y′(0) = 1, k = 3.

Ответ: y = x + 2 x3 + 16 x5 + ...

3! 5!

6.Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию

f(х), заданную на отрезке [−π; π] .

f ( x) =

−π ≤ x < 0,

4x − 3,

0 ≤ x ≤ π.

Ответ:

2π − 3

∞

cos((2k −1) x)

2(2π − 3)

∞

sin (2kx)

f ( x) =

−

∑

sin ((2k −1) x)

− 4∑

(2k −1)2

π k =1

k =1

2k −1

k =1

294

Вариант 10

1.Разложить в ряд Маклорена функцию f(x), указать область сходимо-

сти f ( x) =	1		.


		ex
			∞	(−1)n xn	x	< ∞ .
			Ответ: ∑	,	x	< ∞ .
			n=0	2n n!
			n=0	2n n!

2. Вычислить указанную величину приближенно с заданной точностью δ, используя разложение в степенной ряд соответствующим образом по- добранной функции. е2, δ = 0,001.

Ответ: 7,389. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

0,5	dx
0∫
		.
	1 + x5

Ответ: 0,484. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = x2 + y2 , y (0) = 1.

Ответ: y = 1 + x + x2 + ...

′	= 2x + cos y , y (0) = 0 , k =	5.
y	= 2x + cos y , y (0) = 0 , k =	5.
	Ответ:	y = x + x2 −	x3	−	x4	+ ...
	Ответ:	y = x + x2 −		−		+ ...
		6		4

6.Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию

f(х), заданную на отрезке					[−π; π] .
					f ( x) = 5 − x,
					0,
		2	∞
f ( x) = π + 10	−		∑	cos ((2k −1) x)		−

4		π k =1			(2k −1)2

−π ≤ x ≤ 0, 0 < x ≤ π.

				Ответ:
π + 10	∞	sin ((2k −1) x)	∞	sin (2kx)
	∑		+ ∑		.
π		2k −1
	k =1		k =1	2k

295

Вариант 11

1.	Разложить в ряд Маклорена функцию f(x), указать область сходимо-
сти	f ( x) = sh x .
	∞	x	2n−1			< ∞ .
	Ответ: ∑	x		,	x
	Ответ: ∑	(2n − 1)!		,	x
	n=1
	n=1

2. Вычислить указанную величину приближенно с заданной точностью δ, используя разложение в степенной ряд соответствующим образом по- добранной функции. cos 2°, δ = 0,001.

Ответ: 0,999. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

1	3 1 +	x	2
∫				dx .

0	4

Ответ: 1,026. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y¢ = x2 y2 + y sin x , y (0) = 1 . 2

Ответ: y = 1 + 1 x2 + x3 + ...

2 4 12

y¢¢¢ = yex - xy¢2 , y (0) = 1 , y′(0) =	y′′(0) = 1,			k = 6.
Ответ: y =1	+ x +	x2	+	x3	+	x4	+ 0 × x5 + ...
				3!
	2!				4!

6. Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию f(х), заданную на отрезке [−π; π] .

f ( x) = 0,

−π ≤ x < 0,

0 ≤ x ≤ π.

3x − 1,

f ( x) = 3p - 2 - 6 ∑ cos((2k -1) x)

+ 3p - 2 ∑ sin ((2k -1) x)

Ответ:

- 3∑ sin (2kx) .

∞

k =1

(2k -1)2

k =1

2k -1

k =1 2k

296

Вариант 12

1.	Разложить в ряд Маклорена функцию f(x), указать область сходимо-
сти	f ( x) = e− x4 .
	∞	(−1)n x4n	x	< ∞ .
	Ответ: ∑	,	x	< ∞ .
	n=0	n!
	n=0	n!

2. Вычислить указанную величину приближенно с заданной точностью δ, используя разложение в степенной ряд соответствующим образом по-

добранной функции. 3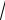80 , δ = 0,001.

Ответ: 4,309. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

0,5∫ sin x2 dx .

0 x

Ответ: 0,493. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = 2 y2 + yex , y (0) = 1 . 3

Ответ: y = 1 + 5 x + 22 x2 + ...

3 9 27

′	= 3x − y	2	,	y (0) = 2 , k = 3.
y

Ответ: y = 2 − 4x + 19 x2 − ...

2 6. Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию f(х), заданную на отрезке [−π; π] .

f ( x) = 3 − 2x, −π ≤ x ≤ 0,

0 < x ≤ π.

f ( x) =

π + 3 − 4 ∑ cos((2k −1) x)

− 2

(π + 3) ∑ sin

((2k −1) x)

Ответ:

+ ∑ sin (2kx) .

∞

k =1

(2k −1)2

k =1

2k −1

k =1 k

297

Вариант 13

1. Разложить в ряд Маклорена функцию f(x), указать область сходимо- сти f ( x) = 2− x2 .

∞	(−1)n lnn 2	2n ,	x	< ∞ .
Ответ: ∑	x	2n ,	x	< ∞ .
n=0	n!
n=0	n!

2. Вычислить указанную величину приближенно с заданной точностью δ, используя разложение в степенной ряд соответствующим образом по- добранной функции. ln 5, δ = 0,001.

Ответ: 1,609. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

0,1∫ ex −1 dx .

0 x

Ответ: 0,103. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = e3x + 2xy2 , y (0) = 1.

Ответ: y = 1 + x + 5 x2 + ...

y′′ = xyy′ , y (0) = y′(0) = 1, k = 6.
Ответ: y = 1 + x +	x3	+	2x4	+	3x5	+ ...

3!		4!		5!

6. Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию f(х), заданную на отрезке [−π; π] .

	0,		−π ≤ x < 0,
f ( x) =	π − x		0 ≤ x ≤ π.
		,
	2	,
	2

Ответ: f ( x) = π +	1	∞	cos((2k −1) x)	+	1	∞	sin (kx)
		∑				∑		.
			(2k −1)2
8 π k =1					2 k =1		k

298

Вариант 14

1. Разложить в ряд Маклорена функцию f(x), указать область сходимо- сти f ( x) = 5x .

∞		n	ln	n	5
Ответ: ∑	x					,	x	< ∞ .
	x
			n!
n=0
n=0

добранной функции. arctg	1	, δ = 0,001.

2

Ответ: 0,464. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

0,5

∫ x2 cos3x dx .

Ответ: 0,018. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = x + ey ,	y (0) = 0 .
	Ответ: y = x + x2 +	1	x3 + ...

	2

′	= x	2	− 2 y , y (0) = 1 , k = 3.
y

Ответ: y = 1 − 2x + 2x2 + ...

6. Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию f(х), заданную на отрезке [−π; π] .


					f ( x) = 5x + 1, −π ≤ x ≤ 0,
						0,		0 < x ≤ π.
	2 − 5π		10	∞	cos((2k −1) x)		5π − 2		∞
f ( x) =		+		∑		+			∑	sin ((2k −1) x)
					(2k −1)2
4			π k =1				π		k =1		2k −1

	Ответ:
∞	sin (2kx)
− 5∑		.

k =1	2k

299

Вариант 15

1.Разложить в ряд Маклорена функцию f(x), указать область сходимо-

сти f ( x) = x cos x .

∞	(−1)n xn+1
Ответ: ∑	, 0 ≤ x < +∞ .
n=0	(2n)!

добранной функции. 6738 , δ = 0,001.

Ответ: 3,006. 3. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.

0,5 ( + 2 )

∫ ln 1 x dx .

Ответ: 0,385. 4. Найти разложение в степенной ряд по степеням х решения диффе- ренциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

y′ = y cos x + 2cos y , y (0) = 0 .

Ответ: y = 2x + x2 − x3 + ...

y′′ = y′ − 1 , y (1) = 1, y′(1) = 0 , k = 4.

Ответ: y = 1 − ( x −1)2 − 2( x −1)4 + 6( x −1)5 + ...

2! 4! 5!

6. Разложить в ряд Фурье периодическую (с периодом ω = 2π ) функцию f(х), заданную на отрезке [−π; π] .

					f ( x) =	0,		−π ≤ x < 0,
					1 − 4x,			0 ≤ x ≤ π.

	1 − 2π		8	∞	cos((2k −1) x)		2	− 4π	∞
f ( x) =		+		∑		+			∑	sin ((2k −1) x)
					(2k −1)2			π
2			π k =1						k =1		2k −1

	Ответ:
∞	sin (2kx)
+ 4 ∑		.

k =1	2k

300

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 2930 / 3330 31 32 33 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20155.38 Mб62умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб63умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб71умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб51умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб61умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб109умк_Яско_ Диф.уравнения_Ряды.pdf