Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Яско_ Диф.уравнения_Ряды

.pdf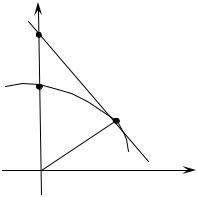

Скачиваний:

Добавлен:

18.05.2015

Размер:

3.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 339 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

3. Решить задачу: Найти кривую, про-						у
ходящую через точку А(0, 1), для которой тре-
угольник, образованный осью Оу, касательной к						N
кривой в произвольной ее точке и радиус-
вектором точки касания, –					равнобедренный	А	М(х, у)
(причем, основанием его служит отрезок каса-
тельной от точки касания до оси Оу).
Указание: Согласно условию
	ON	=	OM	.		0	х

		Ответ:			x2 = 4(1 - y ).

III.Линейные дифференциальные уравнения первого порядка

иуравнение Бернулли

1. Краткий теоретический обзор с использованием лекционного ма- териала, графической схемы, информационной таблицы. Обратить внима- ние, что линейные дифференциальные уравнения и уравнения Бернулли можно решать одним и тем же методом: либо методом подстановки (Бер- нулли), либо методом вариации произвольного постоянного (Лагранжа).

y′ + p ( x) y = f ( x) - линейное дифференциальное уравнение первого

порядка,

y¢ + p ( x) y = f ( x) yn

(n ¹ 0, 1) - дифференциальное уравнение Бер-

нулли.

2. Обучающая задача 1 (решает преподаватель у доски). В

любой момент времени t

скорость v

точки превышает среднюю скорость

за время t с начала движения на величину

t 2 . Найти закон движения, ес-

ли при t = 0 S = S0, v = 0.

Решение. Скорость в момент времени t

будет v =

. Средняя

S − S0

скорость за время t

с начала движения v

. По условию задачи

ср

v - v = t2 . Отсюда дифференциальное уравнение движения

ср

S − S0

= t 2 или

S = t2 -

Получили линейное дифференциальное уравнение первого порядка

(S¢ + p (t ) S = q (t )) . Решим его методом вариации произвольного постоян-

ного (Лагранжа). Для этого сначала решим однородное дифференциальное

уравнение, соответствующее полученному, т.е. уравнение dS - 1 S = 0 . dt t

Так как линейное однородное дифференциальное уравнение в то же время является уравнением с разделяющимися переменными, легко полу-

чаем

∫

= ∫

+ ln C ln

= ln

+ ln

S = Ct

–

общее решение однородного уравнения. Применяя метод вариа-

ции произвольного постоянного, общее решение неоднородного уравнения

ищем в виде S = C (t )t , тогда S′ = C′(t )t + C (t )

C¢(t )t + C (t ) -

C (t )t = t2 -

t ×C¢(t ) = t 2 -

∫dC (t ) = ∫tdt - S0 ∫

+ C1

C (t ) =

+ C1 .

Общим решением неоднородного дифференциального уравнения бу-

дет функция (S = C (t )t )

S =

+ C

или S =

+ C t + S

Начальное условие:

t = 0,

v =

= 0 . Дифференцируя общее реше-

ние, получаем

t 2 + C , откуда

0 =

× 02 + C С1 = 0.

Таким образом,

S = S0 +

–

искомый закон движения.

Обучающая задача 2 .

Проинтегрировать уравнение

y = xy′ + y′ln y .

Решение. Это уравнение не является линейным относительно у и y′ . Но его легко решить, если поменять в нем ролями х и у: принять за ар-

гумент у, а за неизвестную функцию

х. Так как y¢ =

, то y =

( x + ln y )

x¢

x + ln y

x¢ =

x¢ -

x =

ln y

–

линейное дифференциальное уравне-

ние относительно х и x′ . Решим его методом подстановки Бернулли, т.е.

общее решение ищем в виде x =

	1		ln y
u¢v + uv¢ -		uv =		u¢v + u v¢ -
	y		y

u ( y ) × v ( y )				x	′	′	′	Тогда
u ( y ) × v ( y )				x		= u v + uv .		Тогда
		ln y
1 v	=	ln y	.
1 v	=		.
y		y

Выберем v(y)

таким образом, чтобы

v¢ -

v = 0 .

В результате по-

v¢ -

= 0,

лучаем систему:

u¢v =

ln y

Решая первое

уравнение,

получим

∫

= ∫

(берем С = 0)

= ln

v = y.

× y =

ln y

v = y

Подставим

во второе уравнение системы

u = ln y;

dv =

ln y

du =

u =

∫

dy + C =

= -

ln y + ∫

+ C =

du1 =

= -

;

= -

ln y -

+ C

(применена

формула

интегрирования по

частям

∫udv = uv - ∫vdu ).

				1			1
Так как x = u ( y ) × v ( y ) , то x = y C -				1	ln y -		1	, т.е. x = Cy −1 − ln y –
Так как x = u ( y ) × v ( y ) , то x = y C -					ln y -			, т.е. x = Cy −1 − ln y –
				y			y
искомое общее решение.
3.	Два студента у доски (параллельно)					решают (первый пример –
методом Бернулли, второй –		методом Лагранжа):
а)	y¢ - y × th x = ch2 x .					Ответ:			y = ch x (sh x + C ) ;
б)	y¢cos2 x + y = tg x ,	у(0) = 0.				Ответ:			y = tg x + e− tg x -1.
4.	Решить самостоятельно следующие два примера (желательно раз-
ными методами):
а)	(1 + x2 ) y¢ + y = arctg x .		Ответ: y = arctg x + Ce− arctg x -1;

б)	y¢(x + y	2 ) = y .	Ответ: x = Cy + y2 .
5.	Обуча	ющая задача 3	(начинает решать ее преподаватель у

доски). Решить уравнение y¢ + 1 y = x2 y4 . x

Решение. Это уравнение Бернулли ( y¢ + p ( x) y = q ( x) yn ), где n = 4.

Разделим обе части уравнения на у4 или умножим на у– 4 : y−4 × y¢ + 1 × y−3 = x2 .

Пусть z = y−3

z¢ = -3y−4 × y¢ (так как у = у(х) –

функция). Умно-

жив обе части

последнего

уравнения

на

(–3),

получим:

-3y−4 × y¢ - 3

y−3 = -3x2 z¢ -

z = -3x2

является линейным диффе-

z′ .

ренциальным уравнением относительно z и

Далее студенты решают это уравнение самостоятельно, не забывая

вернуться к неизвестной функции у,

подставляя вместо

z = y−3 .

Ответ: y =1

x 3 3ln

6. Решить дифференциальное уравнение y¢ -

2xy

= 4

arctg x

1 + x2

(один студент у доски решает это уравнение методом Лагранжа, второй –

методом Бернулли, не сводя его к линейному).

Ответ: y = (1 + x2 )(arctg2 x + C )2 – общее решение.

Домашнее задание

1.Подготовка теоретического материала по теме «Дифференциаль- ные уравнения в полных дифференциалах».

2.Решить уравнения:

		Ответ: y = e− arcsin x + arcsin x -1;
а)	y¢ 1 - x2 + y = arcsin x , у(0) = 0.	Ответ: y = e− arcsin x + arcsin x -1;
б)	(2xy + 3) dy - y2dx = 0 .	Ответ: x = Cy2 -		1	;
б)	(2xy + 3) dy - y2dx = 0 .	Ответ: x = Cy2 -			;
				y
в)	ydx + (x + x2 y2 )dy = 0 .	Ответ: x =	1			.
в)	ydx + (x + x2 y2 )dy = 0 .	Ответ: x =	y ( y + C )			.
			y ( y + C )

3. Решить задачу: Скорость v, путь S и время t связаны урав- нением v cost + S sin t = 1. Найти закон движения, если при t = 0, S = 2.

Ответ: S = sin t + 2cost . 4. Решить задачу, приводящую к уравнению Бернулли. Среднее гео- метрическое координат точки касания равно отношению отрезка, отсекае- мого касательной на оси ординат, к удвоенной ординате точки касания.

Найти уравнение кривой, если она проходит через точку (1,1).

		y - x × y	′
	xy =		′
Ответ: дифференциальное уравнение имеет вид				,
Ответ: дифференциальное уравнение имеет вид		2 y		,
		2 y
его частное решение ху = 1 и x − y ( x − 2)2 = 0 .

IV. Дифференциальные уравнения в полных дифференциалах. Решение задач прикладного содержания

1. Краткое повторение теоретического материала. Дифференциаль- ное уравнение вида P ( x, y )dx + Q ( x, y )dy = 0 называется дифференци-

альным уравнением в полных дифференциалах, если существует функция

двух переменных	u ( x, y ) ,	что	ее	полный	дифференциал
du ( x, y ) = P ( x, y )dx + Q ( x, y )dy .		Тогда	уравнение		принимает вид
du ( x, y ) = 0 u ( x, y ) = C – его общий интеграл.
Необходимым и достаточным условием				u ( x, y )	является тожде-

¶P ≡ ¶Q

ство ∂y ∂x .

Неизвестную функцию

u ( x, y ) =

u ( x,

∫ P (

y ) можно найти по одной из двух формул:

x, y )dx + ∫ Q ( x0 , y )dy ,

x, y0 )dx + ∫ Q ( x, y )dy ,

где точка M 0 ( x0 , y0 ) – произвольная точка из области существования ре-

шения данного дифференциального уравнения, чаще всего M 0 (0,0).

Обучающий пример 1 . Найти общий интеграл уравнения

( x + y −1)dx + (e y + x)dy = 0 .

Решение. Здесь P ( x, y ) = x + y −1, Q ( x, y ) = e y + x ,	∂P = 1,	∂Q = 1,
	∂y	∂x

следовательно, данное уравнение является уравнением в полных диффе- ренциалах.

(

)

∫

u ( x, y ) =

( x + y

−1)dx +

e y + 0

dy =

( y −1) x

+ e y

+ ( y −1) x + e y −1.

Можно сделать

проверку

правильности

нахождения

функции

u ( x, y ) . du = ( x + y −1)dx + (e y + x)dy , т.е.

du ( x, y ) =

∂u dx +

∂u dy = ( x + y −1)dx + (e y + x)dy .

∂x

∂y

Должны выполняться равенства

∂u = x + y −1 и

∂u = e y + x .

∂x

∂y

верим, так ли это?

′

∂u =

+ ( y −1) x + e y −1

= x + y −1;

∂x

′

∂u =

+ ( y −1) x + e y −1

= x + e y .

∂y

Значит, функция u ( x, y ) найдена верно, и

+ ( y −1) x + e y = C

Про-

есть

общий интеграл данного уравнения.

Дифференциальное уравнение в полных дифференциалах можно ре- шить и другим способом, рассмотрим его на примере.

Обучающий пример 2 . Найти общий интеграл уравнения

(ex + y + sin y )dx + (e y + x + x cos y )dy = 0 .

Решение. Здесь P ( x, y ) = ex + y + sin y , Q ( x, y ) = e y + x + x cos y ,

∂P = 1 + cos y ,	∂Q = 1 + cos y . Следовательно, левая часть есть полный диф-
∂y	∂x
ференциал некоторой функции u ( x, y ) ,		т.е.
	∂u = ex + y + sin y ;	∂u = e y + x + x cos y .
	dx	∂y

Проинтегрируем ∂u по х:

			dx
u = ∫(ex + y + sin y )dx + C ( y ) = ex + yx + x sin y + C ( y ) (С(у)											может
зависеть от у, так как			∂C ( y )	= 0 ). Из последнего выражения находим ча-
зависеть от у, так как			∂x	= 0 ). Из последнего выражения находим ча-
			∂x
			∂u	′	( y )
				′
стную	производную		∂y = x + x cos y + C			и	приравниваем				ее к
∂u = e y + x + x cos y по условию. В результате, имеем
∂y
x + x cos y + C′( y ) = x + x cos y + e y C′( y ) = e y								C ( y ) = e y + C1 .
Таким образом,		u ( x, y ) = ex + yx + x sin y + e y + C ,								а общий интеграл
							1
исходного уравнения имеет вид ex + yx + x sin y + e y = C										(С1 включена в С).
2. Два студента у доски (параллельно) решают примеры:
а)	(x2 + y2 + y )dx + (2xy + x + e y )dy = 0 ,					у(0) = 0 (первым способом).
					Ответ:			1	x3 + xy2 + xy + e y = 1.
					Ответ:				x3 + xy2 + xy + e y = 1.
							3
б)	(3x2 y + sin x)dx + (x3 − cos y )dy = 0 (вторым способом).

Ответ: x3 y − cos x − sin y = C .

3. Решить любым способом следующие примеры (студенты решают самостоятельно с консультациями преподавателя).

	x	2
а) ( y + x ln y )dx +	x
а) ( y + x ln y )dx +	2 y
	2 y

		x	2	ln y + y ( x + 1) = C ;
+ x + 1 dy = 0 .	Ответ:	x
+ x + 1 dy = 0 .	Ответ:
	2

		y					x
б)				− y dx + e y − x −					dy = 0 .
	2		2			2
		+ y			x		+ y	2
x

Ответ: arctg x − xy + e y = C . y

4. Обучающая задача 1 (решает преподаватель у доски). Ис- точник света помещен в точке О. Какова должна быть форма зеркала, что- бы отраженные от него лучи были параллельны оси Ох?

Решение. Воспользуемся решением обучающей задачи 2 из прак- тического занятия II. Там мы при решении этой же задачи получили диф-

ференциальное уравнение y¢ =		y
			,	которое решали как одно-

	x +	x2 + y2

родное. Покажем, что его можно решить как дифференциальное уравнение в полных дифференциалах. Для этого уравнение преобразуем следующим образом:

y (x -

)

y (x -

)

x2 + y2

y¢ = (x +

)(x -

) y¢ =

x2 - x2 - y2

x2 + y2

+ y2

- x

x + y × y′

y¢ =

y¢ × y

+ x =

+ y

x2 + y2

d (

)

+ y

=1 x

+ y

= x + C

или

= 2C x +

Определить тип дифференциального уравнения первого порядка,

указать метод его решения:

а) 4xy¢ + 3y = -ex x4 y5 ;

б)

(arcsin x + 2xy )dx + (x2 +1 + arctg y )dy = 0 ;

в) xy¢ = 2( y -

) ;

г) ( x - 2 y + 3) dy + (2x + y -1) dx = 0 ;

д) 5ex tg y dx + (1 - ex )

dy = 0 ;

cos2

е) ( y4 + 2x) y¢ = y .

Домашнее задание

1.Подготовка теоретического материала по теме «Дифференциаль- ные уравнения высших порядков, допускающие понижение порядка».

2.Решить уравнения:

а) ( x + sin y )dx + ( x cos y + sin y )dy = 0 .

Ответ: x2 + x sin y - cos y = C ; 2

		x			x
б)	ln		− 5 y2 sin 5x dx +	−		+ 2 y cos5x dy = 0 ,	у(1) = 1.
		y			y

	Ответ: x ln	x	+ y2 cos5x − x = cos5 −1;

		y
в)	(ex+ y + 3x2 )dx + (ex+ y + 4 y3 )dy = 0 . у(0) = 0.
		Ответ: ex+ y + x3 + y4 = 1.
3.	Доказать, что уравнение P ( x, y )dx + Q ( x, y )dy = 0 , которое одно-

временно является и однородным, и уравнением в полных дифференциа-

лах имеет общий интеграл x P ( x, y ) + y Q ( x, y ) = C .

Указание. Воспользоваться		теоремой Эйлера об однородных
функциях x ∂P + y ∂P = t P ( x, y ) , где		t – показатель однородности функ-
dx	dy
ций P ( x, y ) и	Q ( x, y ) .

Трехуровневые тестовые задания к разделу « Дифференциальные уравнения первого порядка»

Могут быть использованы для индивидуальных заданий на практи- ческих занятиях, индивидуальных домашних заданий, а также для выпол- нения внеаудиторной контрольной работы (типового расчета, расчетно- графической работы), если она предусмотрена рабочим учебным планом для данной специальности.

Уровень I

Вариант 1

Найти общее решение (общий интеграл) или частное решение (част- ный интеграл) дифференциальных уравнений:

ex+3 ydy = xdx .

Ответ: e3 y = 3(C − xe− x − e− x );

(xy + x3 y ) y′ = 1 + y2 .

;

Ответ: Cx =

(1 + x2 )(1 + y2 )

y − xy′ = x sec

Ответ: sin

= ln

;

(x2 + 1) y′ + 4xy = 3, y (0) = 0 .

Ответ: y =

(x3

+ 3x)

;

(x2 +1)2

y¢ + y = x

Ответ: y =

xe 2

- 2e 2 + C e− x ;

+ S sin t = sin tecos t .

Ответ: S = ecos t (C - cost ) .

Вариант 2

Найти общее решение (общий интеграл) или частное решение (част-

ный интеграл) дифференциальных уравнений:

y′sin x = y ln y .

Ответ: ln y = C tg

;

y′

Ответ: 7− y = 3 × 7− x + C ln 7 ;

= 3 .

y − x

Ответ: ( y2 - x2 )2 = Cx2 y3 ;

( y2 - 3x2 )dy + 2xydx = 0 .

y′ + y tg x = sec x ,

y (0) = 0 .

Ответ: y = sin x ;

( y tg y + ln

cos y

+ C )2

ydx + 2xdy = 2 y

x sec2 ydy .

Ответ: x =

;

(1 - y2 ) y¢ - xy - axy2 = 0 .

Ответ: (C

- a) y =1.

1 - x2

Вариант 3

Найти общее решение (общий интеграл) или частное решение (част-

ный интеграл) дифференциальных уравнений:

y′ = (2x -1) ctg y .

Ответ: ln

cos y

= x - x2 + C ;

y - xy¢ = 2(1 + x2 y¢).

Ответ: y =

+ 2 ;

2x +

( x + 2 y )dx - xdy = 0 .

Ответ: y = Cx2 - x ;

(1 - x)( y¢ + y ) = e− x , y (0) = 0 .

Ответ: y = e− x ln

;

- x

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 339 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20155.38 Mб48умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб49умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб57умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб37умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб47умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб95умк_Яско_ Диф.уравнения_Ряды.pdf