
14-es_1 / Высшая математика (РТФ) / умк_Яско_ Диф.уравнения_Ряды
.pdfVIII. Разложение функций в ряд Фурье, заданных на [– π, π]
Рядом Фурье на [– π, π] называется ряд вида
a0 |
∞ |
(an cos nx + bn sin nx) , |
|
+ ∑ |
|||
|
|||
2 n=1 |
|
||
где a0, an, bn – коэффициенты, вычисляемые по формулам:
a |
|
|
= |
1 |
π |
f ( x)dx , |
|||
|
|
|
∫ |
||||||
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
π |
|
||
|
|
|
|
|
|
|
−π |
|
|
an = |
1 |
π |
f ( x)cos nx dx , |
||||||
∫ |
|||||||||
|
|
|
|
||||||
|
|
π |
|
|
|||||
|
|
|
|
|
−π |
|
|
||
b = |
1 |
|
π |
f ( x)sin nx dx . |
|||||
π |
∫ |
||||||||
n |
|
|
|||||||
|
−π |
|
|
||||||
|
|
|
|
|
|
|
|||
(1)
(2)
(3)
(4)
Если функция f(х) удовлетворяет условиям теоремы Дирихле (смотри теоретическую часть модуля), то ряд справа в формуле (1) сходит- ся к этой функции; в точках непрерывности сумма этого ряда равна значе-
нию функции в этих точках. Если х = х0 |
– точка разрыва I рода, то |
|||||||||||||
|
|
|
|
S ( x0 ) = |
f ( x0 |
− 0) |
+ f ( x0 + 0) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если функция |
f(х) – |
четная, |
то она раскладывается в ряд Фурье |
|||||||||||
только по косинусам, тогда |
|
|
|
|
|
|
|
|
|
|
||||
a |
= |
2 |
π |
f ( x)dx |
, a |
|
= |
2 |
π f ( x)cos nx dx , bn = 0. |
|||||
|
∫ |
n |
|
|||||||||||
0 |
|
π |
|
|
|
|
π |
∫ |
|
|
|
|
||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если функция |
f(х) – |
нечетная, то она раскладывается в ряд Фурье |
||||||||||||
только по синусам, тогда |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
a0 = 0, |
an = 0, |
|
b |
= |
2 |
π f ( x)sin nx dx . |
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
π |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Обучающий пример 1 |
|
(решает преподаватель у доски). |
||||||||||||
Разложить в ряд Фурье 2π-периодическую функцию, заданную на [– π, π]
уравнением f ( x) = x + π .
Решение.
Функция кусочно-монотонная и ограниченная.
261

у
2π
π
−3π |
−2π |
−π |
0 |
π |
2π |
3π |
х |
Определим коэффициенты ряда Фурье:
|
|
|
|
|
|
|
1 |
|
π |
1 |
|
π |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
π |
|
1 |
|
(π2 + π2 ) = 2π ; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
a0 = |
|
∫ f ( x)dx = |
|
∫ |
( x + π)dx = |
|
x |
|
+ πx |
|
|
= |
|
|
||||||||||||||||||||||||||||||||||
|
π |
|
π |
|
|
|
|
|
|
π |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
−π |
|
−π |
|
|
|
|
|
|
|
π |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
π |
|
|
|
|
|
|
|
|
|
|
1 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
u = x + π, |
dv = cos nx dx |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
an |
= |
|
|
∫ |
|
f ( x)cos nx dx = |
|
|
∫ ( x + π)cos nx dx = |
|
|
|
|
|
|
|
|
sin nx |
= |
||||||||||||||||||||||||||||||
π |
|
|
π |
|
du = dx, |
|
v = |
||||||||||||||||||||||||||||||||||||||||||
|
|
−π |
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
1 |
|
|
( x + π)sin nx |
|
π |
− |
1 |
π |
|
|
|
|
= (так как sin nπ = 0 n ) = |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ sin nxdx |
|
|||||||||||||||||||||||||||||||
|
|
π |
n |
|
|
|
|
|
|
|
n |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
−π |
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
π |
1 |
(cos nπ − cos nπ) = 0 . |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
cos nx |
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
πn2 |
|
πn2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
u = x + π, |
|
dv = sin nx dx |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
b |
= |
1 |
|
|
π |
|
|
f ( x)sin nx dx = |
1 |
|
π |
( x + π)sin nx dx = |
|
|
|
|
= |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
π |
|
|
∫ |
|
|
π |
|
∫ |
|
|
|
|
|
|
v = − |
cos nx |
|
|
|||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du = dx, |
|
|
|
|
||||||||||||||||||
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
1 |
|
− |
( x + π)cos nx |
|
π |
+ |
1 |
π |
|
= |
1 |
|
−2πcos nπ |
+ |
1 |
|
π |
|
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
∫ |
cos nxdx |
|
|
|
|
|
sin nx |
|
|||||
|
n |
|
|
n |
|
n |
|
2 |
|
||||||||||
|
π |
|
|
−π |
|
−π |
|
|
π |
|
n |
|
|
−π |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= − |
2 |
cos nπ = − |
2 |
(−1)n = |
2 |
(−1)n+1 . |
|
|
|
||||
|
n |
n |
|
|
|
||||||||
|
|
n |
|
|
|
|
|
|
|
|
|||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
(−1)n+1 |
|
|
|
|
|
sin 2x |
|
sin 3x |
|
|||
π − x = π + 2∑ |
|
|
|
sin nx = π + 2 |
sin x − |
|
+ |
|
− ... . |
||||
|
n |
2 |
3 |
||||||||||
n=1 |
|
|
|
|
|
|
|
|
|||||
=
262

В точке разрыва х = π S (π) = f (π − 0) + f (π + 0) = 2π + 0 = π . 2 2
2.Студенты у доски решают примеры:
1)Разложить в ряд Фурье функцию
имеющую период 2π.
f ( x) = x |
при − π ≤ x ≤ 0, |
2x |
при 0 < x < π, |
Ответ: π − |
2 |
∞ |
cos(2n −1) x |
∞ |
(−1)n−1 |
sin nx |
|
||||||||
∑ |
+ 3∑ |
; |
|||||||||||||
|
|
|
|
||||||||||||
4 |
|
π n=1 |
(2n −1)2 |
|
n=1 |
|
|
|
n |
||||||
2) Разложить в ряд Фурье функцию f ( x) = −x |
|
при − π < x ≤ 0, |
|||||||||||||
|
|
|
|
|
0 |
|
при |
0 < x ≤ π. |
|||||||
Построить графики данной функции и суммы ряда. |
|
|
|
|
|
|
|
||||||||
|
π |
∞ |
(−1)n −1 |
|
|
|
(−1)n |
|
|
||||||
Ответ: |
|
|
+ ∑ |
|
|
|
cos nx + |
|
sin nx . |
||||||
|
|
πn |
|
|
|
||||||||||
|
4 |
|
|
2 |
|
|
|
|
n |
|
|
||||
|
n=1 |
|
|
|
|
|
|
|
|||||||
3) Разложить в ряд Фурье 2π-периодическую функцию f ( x) = x ,
если −π < x ≤ π .
∞ |
(−1)n+1 |
sin nx |
|
|
Ответ: 2 ∑ |
. |
|||
|
||||
n=1 |
|
n |
||
3.Студенты решают самостоятельно:
1)периодическая (с периодом 2π) функция определена следующим
образом |
f ( x) = −1 |
при − π < x < 0, |
|
|
|
Разложить ее в ряд Фурье. |
|
||||||||||||||||||||||
|
1 |
при |
|
0 ≤ x ≤ π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: f ( x) = |
4 |
|
|
|
|
|
|
sin 3x |
|
|
sin 5x |
|
|
sin (2n −1) x |
|
|
|
|||||||||||
|
sin x + |
|
+ |
+ ... + |
+ ... ; |
||||||||||||||||||||||||
|
|
|
|
|
|
(2n −1) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
3 |
|
|
5 |
|
|
|
|
|
|
||||||||
2) |
f ( x) = |
|
x |
|
на [– π, π], 2π-периодическая. Разложить ее в ряд Фурье. |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
cos |
( |
2n −1 x |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
4 |
cos x |
|
|
cos3x |
|
|
|
|
|||||||||||
|
Ответ: f ( x) = |
− |
+ |
+ ... + |
|
|
|
) |
|
+ ... |
; |
||||||||||||||||||
|
2 |
π |
|
|
2 |
2 |
|
|
(2n −1) |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
263

3) Найти |
разложение |
в |
ряд |
|
|
|
Фурье |
функции |
|||
f ( x) = −2 |
при − π < x ≤ 0, |
Построить графики данной функции и сум- |
|||||||||
1 |
при |
0 < x ≤ π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мы ряда. |
|
|
|
|
|
|
|
6 ∞ |
|
|
|
|
|
|
Ответ: f ( x) = − |
1 |
+ |
1 |
sin (2n −1) x . |
||||
|
|
|
|
|
n∑=1 |
|
|||||
|
|
|
2 |
π |
2n −1 |
||||||
Домашнее задание
1.Подготовить теоретический материал по теме «Ряды Фурье для функций, заданных на [−ℓ,ℓ] ».
2.Решить следующие примеры:
а) |
разложить |
в ряд Фурье |
|
2π-периодическую |
функцию |
|||||||||||||||||||||
f ( x) = π + 2x |
при − π < x ≤ 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
−π |
при |
0 < x ≤ π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: − π + |
|
∞ |
|
2 |
|
|
|
|
|
cos(2n −1) x − |
1 |
|
|
||||||||||
|
|
|
2 ∑ |
|
|
|
|
|
|
sin nx |
; |
|||||||||||||||
|
|
|
π(2n − |
1) |
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
б) |
разложить функцию y = x2 |
|
на (0, π) в ряд только по синусам. |
|
||||||||||||||||||||||
|
|
|
|
|
|
∞ |
( |
) |
|
|
|
|
2 |
3 |
(( |
|
|
) |
|
|
|
|
|
|||
|
|
|
|
|
2 |
∑ |
|
π + |
|
|
|
|
) |
|
||||||||||||
|
|
|
Ответ: |
|
|
−1 n+1 |
|
|
2 |
|
|
−1 |
n −1 |
sin nx ; |
||||||||||||
|
|
|
|
π n=1 |
|
|
π |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||||
в) |
разложить функцию y = x3 |
на [– |
|
π, π] в ряд Фурье. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
) |
|
|
3 |
− π |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
∑( |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Ответ: 2 |
|
|
|
−1 |
|
n |
6 |
|
sin nx . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
n |
|
n |
|
|
||||||
IX. Разложение функций в ряд Фурье, заданных на [−ℓ,ℓ]
1. Опрос теоретического материала.
2ℓ-периодическая функция раскладывается в ряд Фурье следующим
образом |
|
∞ |
|
|
|
|
|
|
f ( x) = |
a |
|
nπ |
nπ |
|
|
||
0 |
+ ∑ |
an cos |
|
x + bn sin |
|
x |
, |
|
2 |
|
|
||||||
|
n=1 |
ℓ |
ℓ |
|
|
|||
где a0, an, bn – коэффициенты вычисляются по формулам:
ℓ
a0 = 1 ∫ f ( x)dx ,
ℓ−ℓ
264
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
= |
1 |
|
|
∫ℓ |
|
|
f ( x)cos |
nπ |
x dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
−ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
= |
1 |
|
|
ℓ |
|
|
f ( x)sin |
nπ |
x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Если в ряд Фурье раскладывается четная функция, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a = |
2 |
ℓ f ( x)dx |
, |
|
|
a |
|
|
= |
2 |
|
ℓ f |
( x)cos |
nπ |
|
x dx , |
bn = 0, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
ℓ |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
а если нечетная функция, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а0 = 0, |
|
аn |
= 0, |
|
|
|
|
b |
= |
|
2 |
|
ℓ |
f ( x)sin |
nπ |
x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2. |
|
|
Обучающий пример 1 |
|
|
|
|
|
|
|
(решает преподаватель у доски). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Найти разложение в ряд Фурье функции |
|
|
y = x2 на |
|
[−ℓ,ℓ] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Функция y = x2 |
|
|
– |
|
|
четная, поэтому bn = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
2 |
ℓ |
|
f ( x)dx = |
2 |
|
ℓ x2 dx = |
2 |
|
|
x3 |
|
ℓ |
= |
2 |
|
ℓ2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
||||
|
|
|
2 |
|
ℓ |
( x)cos |
nπ |
|
|
|
|
|
|
|
2 |
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
u = x2 , |
|
|
|
|
|
|
dv = cos |
|
x dx |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
an = |
|
∫ f |
x dx = |
∫ x2 cos |
|
x dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ℓ |
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
nπ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
du = 2xdx, |
v = |
|
sin |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
ℓ |
|
|
|||||||||||||||||||||||||||||||||||
|
2 |
|
|
ℓ |
|
|
2 |
|
|
|
nπ |
|
ℓ |
|
2ℓ |
ℓ |
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
u = x, |
|
|
|
|
|
dv = sin |
nπ |
x dx |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
sin |
|
|
− |
∫ x sin |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
ℓ |
nπ |
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du = dx, |
v = − |
ℓ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
x |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
ℓ |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
ℓ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2ℓ |
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
ℓ |
|
|
ℓ |
|
ℓ |
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
sin nπ − |
|
|
|
|
|
− |
|
|
|
|
|
|
x cos |
|
|
|
|
x |
|
+ |
|
|
|
|
|
|
∫cos |
|
|
xdx |
|
= |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
nπ |
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ℓ |
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
ℓ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ℓ2 |
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
4ℓ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= − |
|
−ℓ2 cos nπ + |
|
|
|
|
|
|
|
sin |
x |
|
= |
|
|
cos nπ , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
π |
|
|
|
|
|
0 |
|
n |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
ℓ |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
так как |
sin nπ = 0 , |
то есть a |
|
= |
|
4ℓ2 ( |
−1)n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
π2 |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
265
Таким образом, |
|
|
2 |
= |
ℓ2 |
+ |
4ℓ2 |
∑ |
(−1)n |
cos |
nπ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
n2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3 |
|
π2 |
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
ℓ2 |
|
|
4ℓ2 |
π |
|
|
|
1 |
|
|
|
|
2π |
|
|
1 |
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
|
|
− |
|
|
|
|
cos |
x − |
|
|
|
|
cos |
|
x + |
|
|
|
cos |
|
|
x − ... . |
|
|
|
|
|
|
|
|
||||||||||||||||
|
3 |
|
|
π2 |
22 |
|
|
32 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
ℓ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3. Студенты у доски решают следующие примеры: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Пример 1. |
|
Найти разложение в ряд Фурье периодической функ- |
||||||||||||||||||||||||||||||||||||||||||||||
ции с периодом 4: |
|
|
|
|
|
f ( x) = −1 |
|
|
при − 2 < x < 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
при |
0 ≤ x ≤ 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: f ( x) = |
1 |
+ |
6 |
|
∞ |
1 |
|
|
|
(2n −1)π |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
sin |
|
|
x . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n − |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
π n=1 |
1 |
|
|
|
|
|
2 |
|
|
|||||||
Пример 2. |
|
Найти разложение в ряд Фурье функции |
f ( x) = −x на |
|||||||||||||||||||||||||||||||||||||||||||||
отрезке [– 2, 2]. Построить графики данной функции и суммы ряда. |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: f ( x) |
∞ (−1)n |
|
nπ |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4 ∑ |
|
|
|
|
|
sin |
|
x . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
n |
2 |
|
||||||||
4. Студенты самостоятельно решают примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Пример 1. |
|
Разложить в ряд Фурье периодическую функцию с пе- |
||||||||||||||||||||||||||||||||||||||||||||||
риодом 2ℓ = 4 , если |
f ( x) = 1 + x |
|
|
при − 2 < x ≤ 0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
при |
|
0 < x ≤ 2. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Ответ: − |
1 |
+ |
2 |
|
∞ |
|
|
|
|
2 |
|
|
|
|
|
|
π(2n −1) x |
− |
1 |
sin πnx |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
cos |
. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
π(2n −1) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
n |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 π n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Пример 2. |
|
Разложить в ряд Фурье только по синусам функцию |
||||||||||||||||||||||||||||||||||||||||||||||
f ( x) = 1 − |
x |
на [0, 2]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ 1 |
πn |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
∑ |
|
|
sin |
x . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π n=1 n |
2 |
|
|||||||
5. Преподаватель у доски отмечает одно важное свойство периоди- ческих функций:
π |
λ+2π |
∫ ϕ( x)dx = ∫ ϕ( x)dx , |
|
−π |
λ |
каким бы ни было число λ.
Это означает, что при вычислении коэффициентов Фурье можно за- менить промежуток интегрирования [– π, π] промежутком [λ, λ + 2π], где λ – любое число.
266
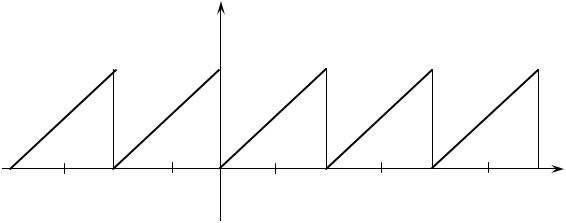
6 . Обучающий пример 1. |
Пусть требуется разложить в ряд |
|||||||||||||||
Фурье функцию |
f(х) с периодом 2π, которая на |
[0, 2π] задана равенст- |
||||||||||||||
вом f(х) = х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
График функции изображен на рисунке. Эта функция на [– π, π] за- |
||||||||||||||||
дается двумя формулами: |
f ( x) = x + 2π |
на [– π, 0] |
и f(х) = х на [0, π]. |
|||||||||||||
Для разложения этой функции выгоднее воспользоваться следую- |
||||||||||||||||
щими формулами (приняв λ = 0): |
|
|
|
|
|
|
|
|
2π = 2π ; |
|||||||
a = |
1 |
λ+2π f ( x)dx = |
1 |
2π f ( x)dx = |
1 |
2π xdx = |
1 |
|
x2 |
|
||||||
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||
0 |
π |
∫ |
|
π |
∫ |
|
π |
∫ |
|
π 2 |
|
|||||
|
λ |
|
0 |
|
0 |
|
0 |
|||||||||
|
|
|
|
|
|
|
|
|||||||||
у
2π
−4π −3π |
|
|
−2π |
|
|
|
−π |
|
0 |
|
|
|
|
|
|
|
π |
|
|
|
|
2π |
|
|
|
|
|
|
3π |
|
|
|
4π |
|
|
|
|
5π |
|
|
|
|
|
6π х |
|||||||||||||||||||||
a |
= |
1 |
|
λ+2π f ( x)cos nxdx = |
1 |
|
2π x cos nxdx = |
|
u = x, |
|
dv = cos nxdx |
|
|
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin nx |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
π |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
du = dx, v = |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
1 |
2π |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
x sin nx |
|
|
− |
|
∫ sin nx = |
|
|
|
|
|
cos nx |
|
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
b |
= |
1 |
λ+2π f |
( x)sin nxdx = |
1 |
2π x sin nxdx = |
|
u = x, |
|
dv = sin nxdx |
|
= |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos nx |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
π |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
∫ |
|
|
|
|
|
|
|
|
|
|
|
du = dx, v = − |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
1 |
|
− |
x cos nx |
|
2π |
+ |
|
1 2π |
|
|
|
|
|
|
|
|
|
= |
1 |
|
|
− |
|
2πcos 2nπ |
+ |
|
1 |
|
|
|
|
|
|
2π |
= − |
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ cos nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin nx |
|
|
|
|
. |
||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
n |
π |
|
|
|
n |
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
sin nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2x |
|
|
sin 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
f ( x) = π − 2 ∑ |
|
|
|
|
|
|
= π − 2 |
sin x |
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
... |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
267

Пусть x = π , имеем
π |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
1 |
|
1 |
|
1 |
|
1 |
− ... + (−1) |
n+1 |
1 |
|
|
||
|
= π − 2 |
1 − |
|
+ |
|
− ... 1 − |
|
+ |
|
|
|
|
+ ... = |
. |
|
2 |
3 |
5 |
3 |
5 |
|
2n −1 |
|||||||||
|
|
|
|
|
|
|
|
4 |
|||||||
|
|
|
|
|
|
Домашнее задание |
|
заданную на [−ℓ,ℓ] |
|||||||
Пример 1. |
Разложить в ряд Фурье функцию, |
||||||||||||||
следующим образом
|
|
|
|
0, |
|||
|
|
|
|
f ( x) = x, |
|||
|
|
|
|
|
ℓ |
||
|
|
, |
|
2 |
|||
|
|
||
если − ℓ≤ x ≤ 0;
если 0 < x ≤ ℓ; 2
если ℓ < x < ℓ. 2
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
πx |
|
2 + π πx |
|
||||||
|
|
|
|
|
|
Ответ: f ( x) = ℓ |
|
|
+ |
− |
|
|
|
cos |
+ |
|
|
sin |
|
+ |
|||||||||
|
|
|
|
|
|
|
|
π2 |
|
2π2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
ℓ |
|
|
|
ℓ |
|
||||||
|
|
1 |
|
2πx |
|
1 |
|
2πx |
|
|
1 |
|
|
3πx |
|
|
−2 + 3π 3πx |
|
|
||||||||||
+ |
− |
|
cos |
|
+ |
|
|
sin |
|
|
+ |
− |
|
|
|
cos |
|
|
|
+ |
|
|
sin |
|
|
|
+ ... . |
||
4π2 |
|
|
4π |
|
9π2 |
|
|
|
18π2 |
|
|
||||||||||||||||||
|
|
|
ℓ |
|
|
|
ℓ |
|
|
|
ℓ |
|
|
|
|
ℓ |
|
|
|
||||||||||
Пример 2. Разложить в ряд Фурье только по косинусам функцию f ( x) = 1 − 2x на [0, 1].
|
8 |
∞ |
cos π(2n −1) x |
|
|
Ответ: |
|
∑ |
|
. |
|
π2 |
(2n −1)2 |
||||
|
n=1 |
|
Трехуровневые тестовые задания к разделу « Ряды»
Могут быть использованы для дополнительных заданий на практи- ческих занятиях, индивидуальных домашних заданий, проведения ауди- торных контрольных работ, а также для индивидуальных заданий для вне- аудиторных самостоятельных работ (контрольных работ, типовых или расчетно-графических работ), если они предусмотрены рабочим учебным планом для данной специальности.
Уровень I
Вариант 1
|
∞ |
1 |
|
|
1. Доказать сходимость ряда и найти его сумму |
∑ |
. |
||
|
||||
|
||||
|
n=1 n(n + 2) |
|
||
Ответ: S = 3 . 4
268

2.Исследовать на сходимость:
|
∞ |
3n (n + 2)! |
|
|||||
а) |
∑ |
|
|
|
|
|
|
. |
|
n5 |
|
|
|||||
|
n=1 |
|
|
|
|
|||
|
|
|
Ответ: расходится; |
|||||
|
∞ |
10 |
n |
|
|
|
||
б) |
∑ |
|
|
. |
|
|
||
n + |
1 n |
|
|
|||||
|
n=1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
|
|
|
|
Ответ: расходится;
∞ |
|
2n +1 |
2 |
||
в) ∑ |
|
|
|
. |
|
4n2 +1 |
|||||
n=1 |
|
||||
Ответ: сходится;
∞ |
1 |
|
|
|
г) ∑ |
|
|
. |
|
|
|
|
||
|
|
|
||
|
||||
n=1 |
n3 + 2 |
|||
Ответ: сходится.
3.Исследовать на абсолютную или условную сходимость
∞ |
(-1)n+1 |
1 |
|
|
∑ |
. |
|||
(n +1) ×3n |
||||
n=1 |
|
|
Ответ: абсолютно сходится.
4.Найти область сходимости рядов:
∞ |
2n |
× xn |
|
|
|
|
∞ |
( x - 4)2n−1 |
|
а) ∑ |
|
|
. |
|
|
|
|
б) ∑ |
. |
|
+1 |
|
|
|
|
||||
n=1 n2 |
|
|
|
|
|
n=1 |
2n -1 |
||
|
|
|
|
1 |
|
1 |
|
|
Ответ: 3 < x < 5 . |
|
|
Ответ: - |
|
; |
|
|
; |
|
|
|
|
2 |
2 |
|
|||||
|
|
|
|
|
|
|
|
||
Вариант 2
|
∞ |
3n + 4n |
|
|
1. Доказать сходимость ряда и найти его сумму |
∑ |
|
. |
|
12n |
||||
|
n=1 |
|
Ответ: S = 5 . 6
2.Исследовать на сходимость:
∞ |
|
7n -1 |
|
∞ |
|
|
|
1 |
|
|
|
|
|
||||
а) ∑ |
|
. |
в) ∑ |
|
|
|
|
|
|
|
. |
||||||
|
|
|
(3n + 2)ln (3n + 2) |
||||||||||||||
n=1 5n (n +1)! |
n=1 |
|
|||||||||||||||
|
|
Ответ: сходится; |
∞ |
|
|
Ответ: расходится; |
|||||||||||
∞ |
|
5n -1 n |
2 |
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
г) ∑ |
|
|
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) ∑ |
|
|
. |
n=1 |
3 |
|
n |
5 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||||||
n=1 |
5n |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Ответ: сходится. |
|||||||||
|
|
Ответ: сходится; |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
(-1)n |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
||||
3. Исследовать на абсолютную или условную сходимость ∑ |
|
|
|
|
. |
||||||||||||
|
|
|
|
||||||||||||||
|
n +1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|||
Ответ: условно сходится.
269

4.Найти область сходимости рядов:
∞ |
nx |
n−1 |
|
|
|
∑∞ ( x - 3) |
n |
||
а) ∑ |
|
|
. |
б) |
. |
|
|||
|
|
|
|||||||
n=1 2n−1 ×3n |
|
|
|
n=1 n ×5n |
|
|
|||
|
|
|
Ответ: (-6, 6); |
|
|
Ответ: −2 ≤ x < 8. |
|||
|
|
|
|
Вариант 3 |
|
|
|
|
|
|
|
|
|
|
|
∞ |
1 |
|
|
1. Доказать сходимость ряда и найти его сумму |
n∑=0 |
|
. |
||||||
|
|||||||||
(2n + 5)(2n + 7) |
|||||||||
Ответ: S = 1 . 10
2.Исследовать на сходимость:
∞ |
|
7 n |
|
1 7 |
|
∞ |
1 |
|
|
|
||||||
а) ∑ |
|
|
|
|
|
. |
|
в) ∑ |
|
|
|
|
|
|
. |
|
|
|
|
|
|
(2n + 1)ln |
3 |
( |
2n + 1) |
||||||||
|
|
|
|
|||||||||||||
n=1 |
8 n |
|
n=1 |
|
|
|
||||||||||
|
|
|
Ответ: сходится; |
|
|
Ответ: сходится; |
||||||||||
∞ |
|
|
|
1 |
|
n |
∞ |
1 |
|
|
|
|
|
|||
б) ∑ |
arctg |
|
|
|
|
. |
г) ∑ |
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
2n + 1 |
|
|
|
|
||||||||||||
n=1 |
|
|
|
n=1 |
|
5n + 2 |
|
|
|
|
||||||
|
|
|
Ответ: сходится; |
|
|
Ответ: расходится. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
(-1)n+1 |
|
3. Исследовать на абсолютную или условную сходимость ∑ |
ln n |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n=2 |
|
|||
Ответ: условно сходится.
4.Найти область сходимости рядов:
∞ |
3n |
|
|
∑∞ ( x - 2) |
n |
|
|||
а) ∑ |
x |
|
. |
б) |
. |
|
|||
|
|
|
|||||||
n=1 8n |
|
|
n=1 2n |
|
|
||||
|
|
|
|
Ответ: (-2, 2); |
|
Ответ: 0 < x < 4 . |
|||
|
|
|
|
Вариант 4 |
|
|
|
|
|
|
|
|
|
|
∞ |
2n + 5n |
|
||
1. Доказать сходимость ряда и найти его сумму |
∑ |
|
|
. |
|||||
10n |
|||||||||
|
|
|
|
|
n=1 |
|
|||
Ответ: S = 5 . 4
270
