
The Physics of Coronory Blood Flow - M. Zamir
.pdf
190 6 Composite Pressure-Flow Relations
pni(t) = (pn(t)) |
(6.4.29) |
= Mn sin |
2πnt |
− φn |
n = 1, 2, . . . , N |
(6.4.30) |
T |
||||
qnr (t) = (qn(t)) |
|
|
(6.4.31) |
|
= |
pn(t) |
n = 1, 2, . . . , N |
(6.4.32) |
||
|
Z |
|
|||
qni(t) = (qn(t)) |
|
(6.4.33) |
|||
= |
pn(t) |
n = 1, 2, . . . , N |
(6.4.34) |
Z |
6.5Composite Pressure-Flow Relations Under Inertial E ects
Inertial e ects are important in coronary blood flow, and in blood flow in general, because of the pulsatile nature of the flow. In pulsatile flow the fluid is repeatedly accelerated and decelerated and hence fluid inertia, or what in previous sections was referred to as the inductance (L), has a significant e ect on the relation between pressure and flow. The origin and basic nature of the inertial e ect were examined in Chapter 2. In Chapter 3 the e ects of inductance on the free dynamics of the RLC system were examined, and the same was done in Chapter 4 for the forced dynamics of the RLC system, using either linear or simple sinusoidal driving pressures. In this section we examine the e ects of inertia on pressure-flow relations when the driving pressure has a composite waveform.
As noted in earlier sections, inertial e ects in the coronary circulation and in the cardiovascular system in general do not arise in pure form but always in combination with resistance e ects and frequently in combination with capacitance e ects. Only when a breach occurs within the vascular system is blood able to accelerate and decelerate free from the constraints of the containing vessels and hence free from resistance and capacitance e ects. It is therefore not meaningful to study the inertial e ect in isolation, that is to study only the inductance element L of the RLC system by itself. In this section we examine the e ects of inductance L in combination with resistance R and in later sections within the complete RLC system.
Consider resistance R and inductance L in series at first, where the complex impedance, from Eqs. 4.9.34, 35, is given by
Z = R + iωL |
(6.5.1) |

6.5 Composite Pressure-Flow Relations Under Inertial E ects |
191 |
where ω is the angular frequency. Since the individual harmonics of a composite wave have di erent frequencies, we should strictly write
Zn = R + iωnL |
(6.5.2) |
ωn = 2πn n = 1, 2, . . . , N |
(6.5.3) |
to highlight the fact that di erent harmonics will have di erent impedances. We also note that in general if we write
Zn = znr + izni n = 1, 2, . . . , N |
(6.5.4) |
where n denotes a particular harmonic, and subscripts r, i denote real and imaginary parts as before, then
znr = R |
(6.5.5) |
zni = ωnL |
(6.5.6) |
In other words, as stated earlier, when R, L are in series, the real part of the impedance for each harmonic represents pure resistance while the imaginary part represents the inertial e ects.
The expression for the real part of the flow rate for individual harmonics can now be put together, using the above notation and the results of the previous section (Eqs. 6.4.11, 28, 30)
pn(t)
qnr (t) = (6.5.7)
Zn
= |
|
pnr + ipni |
|
|
|
(6.5.8) |
|||||
|
znr + izni |
|
|
|
|
|
|||||
= |
pnr znr + pnizni |
|
|
|
|
(6.5.9) |
|||||
|
|
|
|
||||||||
|
|
z2 + z2 |
|
|
|
|
|
||||
|
|
|
nr |
ni |
|
|
|
|
|
||
|
|
|
|
2πnt |
+ ωnL |
|
2πnt |
|
|||
|
|
|
|
|
R |
|
|||||
= |
RMn cos |
T − φn |
+ ωnLMn sin |
T − φn |
(6.5.10) |
||||||
|
2 |
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|||||
When resistance and inductance are in parallel, the above analysis of the flow wave remains intact, with only a change in the form of the impedance. Thus, when R and L are in parallel, we have, from Eqs. 4.9.33–35 and in the notation of the present section,
1 |
= |
1 |
+ |
1 |
|
(6.5.11) |
|
Zn |
R |
iωnL |
|||||
|
|
|
|||||
For easier comparison of the pressure and flow waveforms, it is more convenient to use not the flow rate but the R-scaled flow rate introduced earlier, namely
192 6 Composite Pressure-Flow Relations
|
× |
|
|
2πnt |
1 + ωn2 tL2 |
|
2πnt |
|
||
|
|
|
|
|||||||
R |
|
qnr (t) = |
Mn cos T − φn |
+ ωntLMn sin |
|
T − φn |
(6.5.12) |
|||
|
|
|
|
|
|
|||||
where |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tL = |
L |
|
|
(6.5.13) |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
R |
|
|
|
|
||
is the inertial time constant introduced earlier. We saw in the previous section that when opposition to flow consists of pure resistance the forms of the pressure and of the R-scaled flow are identical. Therefore, in the present section where inertial e ects are present, any deviation from this identity can be attributed directly and entirely to inertial e ects. This highlights the advantage of using the R-scaled flow rate instead of the flow rate for comparison with the pressure waveform. Furthermore, in this way the physical parameters R and L do not need to be specified separately because only their ratio, the inertial time constant tL is now required.
As discussed at great length in Section 2.5, the inertial time constant tL is a measure of the time it takes the fluid to respond to a change in the driving pressure. The unit of time in which tL is expressed depends on the unit of time used for the angular frequency ωn in Eq. 6.5.11. When the frequency is in radians per second, tL must be expressed in seconds so that the product ωntL in Eq. 6.5.11 becomes nondimensional as it should be. Minutes can be used in the same way. In what follows and in much of this book we express tL in seconds. As discussed in earlier sections, while the actual value of tL in the coronary circulation is not known, its order of magnitude is clearly seconds rather than minutes.
Eq. 6.5.11 produces the individual harmonics of the oscillatory part of the R-scaled flow wave. The complete oscillatory flow wave is finally obtained by
adding these harmonics, that is |
|
R × qr (t) = R × q1r (t) + R × q2r (t) . . . + R × qN r (t) |
(6.5.14) |
where N is the number of harmonics. The complete R-scaled flow wave (corresponding to real part of driving pressure) is then given by
R × Q(t) = R × |
|
+ R × qr (t) |
(6.5.15) |
q |
Results, comparing the R-scaled flow wave with the corresponding pressure wave at di erent values of tL, and using the one-step, piecewise, and cardiac pressure waves, are shown in Fig. 6.5.1–3. It is seen that when tL is very small, inertial e ects are insignificant and the forms of the pressure and the R-scaled flow rate become identical. At the other extreme, at higher values of tL, inertial e ects become increasingly more significant as evidenced by the considerable di erence they produce between the forms of the pressure and the R-scaled flow wave. Increasingly, the oscillatory part of the flow wave diminishes, leaving only the steady part, as the value of tL increases.

6.5 Composite Pressure-Flow Relations Under Inertial E ects |
193 |
|
1.5 |
|
|
|
|
|
(mmHg) |
1 |
a |
|
|
|
|
|
|
|
|
|
||
flow |
|
|
|
|
|
|
|
b |
c |
|
|
|
|
|
|
|
|
|
||
|
|
d |
|
|
|
|
R−scaled |
|
|
|
|
|
|
0.5 |
|
e |
|
|
|
|
|
|
|
|
|
|
|
pressure, |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−0.50 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
Fig. 6.5.1. Pressure (solid) and R-scaled flow waves (dashed) through a resistance R and inductance L in series, and for di erent values of the inertial time constant tL in seconds: (a) 0.02, (b) 0.075, (c) 0.16, (d) 0.35, (e) 2.0. At the lowest value of tL, R-scaled flow wave is close to that of pressure, indicating that oscillatory flow is little a ected by the inertia of the fluid, while at the highest value of tL the opposite is true and oscillatory flow is reduced almost to zero, leaving mainly the steady part of the flow.
|
1.5 |
|
|
|
|
|
(mmHg) |
1 |
|
a |
|
|
|
|
|
|
|
|
||
flow |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
c |
|
|
|
|
R−scaled |
0.5 |
|
d |
|
|
|
|
|
e |
|
|
||
|
|
|
|
|
|
|
pressure, |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−0.50 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
Fig. 6.5.2. See caption for Fig. 6.5.1.
194 6 Composite Pressure-Flow Relations
|
115 |
|
|
|
|
|
(mmHg) |
|
|
|
a |
|
|
110 |
|
|
b |
|
|
|
|
|
c |
|
|
||
|
|
|
|
|
||
flow |
105 |
|
d |
|
|
|
R−scaled |
|
|
e |
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
pressure, |
95 |
|
|
|
|
|
|
|
|
|
|
|
|
|
900 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
Fig. 6.5.3. See caption for Fig. 6.5.1.
so that
iωnLR Zn = R + iωnL
ω2 L2R + i(ωnLR2) = n R2 + ωn2 L2
and the real and imaginary parts of the impedance are thus given by
znr = |
ωn2 L2R |
R2 + ω2 L2 |
|
|
n |
zni = |
ωnLR2 |
R2 + ω2 L2 |
|
|
n |
(6.5.16)
(6.5.17)
(6.5.18)
(6.5.19)
These expressions for the complex impedance are now used instead of those in Eqs. 6.5.5, 6 and all subsequent steps are repeated to find that the R-scaled flow wave in this case is given by
|
× |
|
|
2πnt |
|
|
2πnt |
|
|
|
|
ωn L |
|
||||||
R |
|
qnr (t) = |
ωntLMn cos |
T − φn |
+ Mn sin |
|
T − φn |
(6.5.20) |
|
|
|
|
t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
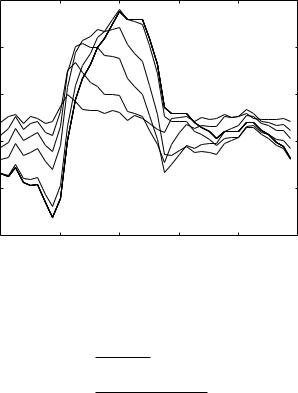
Results for di erent values of the inertial time constant tL, and using the one-step, piecewise, and cardiac pressure wave, are shown in Figs. 6.5.4–6. In contrast with the case of RL in series, it is seen that in this case the forms of the pressure and R-scaled flow waves become identical at higher values of
6.5 Composite Pressure-Flow Relations Under Inertial E ects |
195 |
|
6 |
|
|
a |
|
|
|
|
|
|
|
|
|
(mmHg) |
4 |
|
|
b |
|
|
|
|
c |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
flow |
2 |
|
|
d |
|
|
|
|
e |
|
|
||
R−scaled |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
pressure, |
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
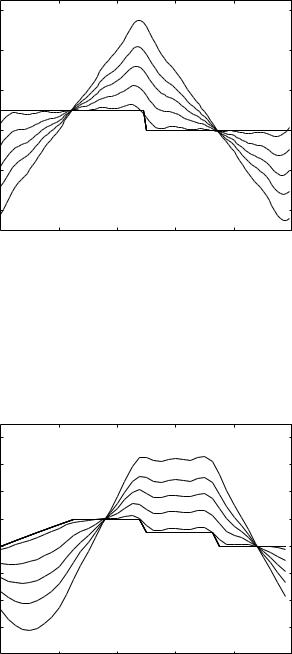
Fig. 6.5.4. Pressure (solid) and R-scaled flow waves (dashed) through a resistance R and inductance L in parallel, and for di erent values of the inertial time constant tL in seconds: (a) 0.025, (b) 0.035, (c) 0.05, (d) 0.09, (e) 0.5. Much larger swings in flow rate are observed in this case, compared with the case of R, L in series, because flow has the option of accelerating or decelerating through the inductor without being constrained by the resistor.
|
4 |
|
|
|
|
|
(mmHg) |
|
|
|
a |
|
|
3 |
|
|
b |
|
|
|
|
|
|
|
|
||
2 |
|
|
c |
|
|
|
flow |
1 |
|
|
d |
|
|
|
|
e |
|
|
||
R−scaled |
|
|
|
|
||
|
|
|
|
|
||
0 |
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
pressure, |
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−40 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
Fig. 6.5.5. See caption for Fig. 6.5.4.
196 6 Composite Pressure-Flow Relations
(mmHg) |
140 |
|
|
|
|
|
120 |
|
|
|
|
|
|
flow |
100 |
|
a |
|
|
|
R−scaled |
|
|
|
|
||
|
|
b |
|
|
|
|
80 |
|
c |
|
|
|
|
pressure, |
60 |
|
d |
|
|
|
|
|
|
|
|
||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
Fig. 6.5.6. See caption for Fig. 6.5.4. Here (a) 0.5, (b) 0.1, (c) 0.06, (d) 0.04, (e) 0.03.
|
6 |
|
|
|
|
|
(mmHg) |
4 |
|
|
a |
|
|
|
|
|
|
|
||
|
|
|
b |
|
|
|
flow |
2 |
|
|
c |
|
|
R−scaled |
|
|
|
d |
|
|
0 |
|
|
e |
|
|
|
|
|
|
|
|
|
|
pressure, |
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
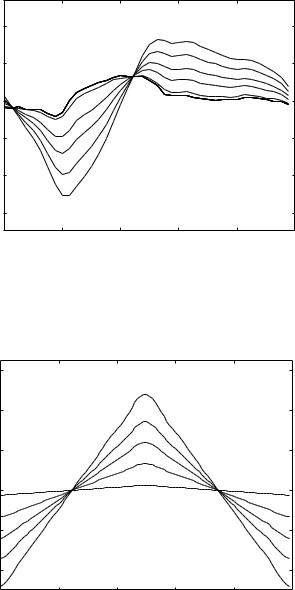
Fig. 6.5.7. R-scaled inductive flow only, produced by the one-step pressure wave of Fig. 6.5.4, and for di erent values of the inertial time constant tL in seconds: (a) 0.025, (b) 0.035, (c) 0.05, (d) 0.09, (e) 0.5. At the highest value of tL inductive flow is near zero, leaving flow mainly through the resistor. At the lowest value of tL inductive flow is high and is in addition to flow through the resistor. Total flow rate through the system is shown in Fig. 6.5.4.

6.5 Composite Pressure-Flow Relations Under Inertial E ects |
197 |
|
4 |
|
|
|
|
|
(mmHg) |
3 |
|
|
a |
|
|
2 |
|
|
b |
|
|
|
|
|
|
|
|
||
flow |
|
|
c |
|
|
|
|
|
|
|
|
||
1 |
|
|
d |
|
|
|
R−scaled |
|
|
|
|
||
0 |
|
|
e |
|
|
|
|
|
|
|
|
||
−1 |
|
|
|
|
|
|
pressure, |
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−40 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
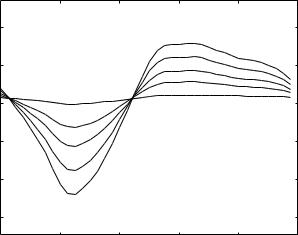
Fig. 6.5.8. R-scaled inductive flow only, produced by the piecewise pressure wave of Fig. 6.5.5, and for di erent values of the inertial time constant tL in seconds: (a) 0.025, (b) 0.035, (c) 0.05, (d) 0.09, (e) 0.5. At the highest value of tL inductive flow is near zero, leaving flow mainly through the resistor. At the lowest value of tL inductive flow is high and is in addition to flow through the resistor. Total flow rate through the system is shown in Fig. 6.5.5.
tL, which represent higher inertial e ects. The reason for this is that when R and L are in parallel, flow has the option of going through the resistor rather than the inductor, so that when inertial e ects become very high the entire flow goes through the resistor and, as seen Section 6.3, the pressure and R- scaled flow waveforms become identical. At the other extreme, when inertial e ects are very low, more of the flow goes through the inductor. Under these conditions much larger swings in flow rate are produced within the oscillatory cycle than are produced when R and L are in series. In that case the flow is constrained because it has to go through the resistor even when values of tL are low.
These observations can be seen more clearly in Figs. 6.5.7–9 where only flow through the inductor is shown. It is seen that flow through the inductor is highest when inertial e ects are low, while it is near zero when inertial e ects are high. The steady part of the flow, of course, does not contribute to flow through the inductor.
It is interesting to note in Figs. 6.5.4–9 that when R, L are in parallel, flow through the inductor can accelerate or decelerate freely, unimpeded by the presence of the resistor. Thus, within an oscillatory cycle, total flow through the system first increases in response to a positive pressure gradient and then decreases as the gradient changes sign, or vice versa, depending on the form of
198 6 Composite Pressure-Flow Relations
(mmHg) |
140 |
|
|
|
|
|
120 |
|
|
|
|
|
|
flow |
100 |
|
|
|
|
|
R−scaled |
|
a |
|
|
|
|
|
|
|
|
|
||
80 |
|
b |
|
|
|
|
|
c |
|
|
|
||
|
|
|
|
|
||
pressure, |
|
|
|
|
|
|
60 |
|
d |
|
|
|
|
|
|
|
|
|
||
|
|
e |
|
|
|
|
|
40 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
time t (normalized) |
|
|
|
Fig. 6.5.9. R-scaled inductive flow only, produced by the cardiac pressure wave of Fig. 6.5.6, and for di erent values of the inertial time constant tL in seconds: (a) 0.5,
(b) 0.1, (c) 0.06, (d) 0.04, (e) 0.03. At the highest value of tL inductive flow is near zero, leaving flow mainly through the resistor. At the lowest value of tL inductive flow is high and is in addition to flow through the resistor. Total flow rate through the system is shown in Fig. 6.5.6.
the pressure wave. The result is that inductive flow will typically go through zero twice within the oscillatory cycle, as seen in Figs. 6.5.7–9.
6.6Composite Pressure-Flow Relations Under Capacitance E ects
Capacitance e ects are important in coronary blood flow because of the pulsatile nature of the flow and because of the elasticity and hence compliance of the coronary vessels. While this statement is equally true in the cardiovascular system as a whole, capacitance e ects play a more critical role in the dynamics of the coronary circulation because of the violent compression e ects which the cardiac muscle exerts on coronary vasculature imbedded within the myocardium. The way this so called “tissue pressure” or “intramyocardial pressure” is intermingled with normal capacitance e ects due to vessel compliance is far from fully understood, which makes the role of capacitance in the coronary circulation all the more critical. Indeed, this is one of the major problems in the modelling of the coronary circulation which we shall consider later. In this section we consider the capacitance e ect without this added complication, with the aim of understanding the e ect pure capacitance has on pressure-flow relations.

6.6 Composite Pressure-Flow Relations Under Capacitance E ects |
199 |
The origin and basic nature of the capacitance e ect were examined in Chapter 2, where the e ect was likened to that of flow going into an elastic balloon. In Chapter 3, the e ects of capacitance on the free dynamics of the RLC system were examined, and the same was done in Chapter 4 for the forced dynamics of the RLC system, using either linear or simple sinusoidal driving pressures. In this section we examine the e ects of capacitance on pressure-flow relations when the driving pressure has a composite waveform.
Using the analogy of flow into an elastic balloon, it was discussed in Section 3.2 that when the balloon is in series with other elements of the RLC system, flow through the system is clearly limited by the capacity of the balloon. It is clear from that section, therefore, that the e ect of capacitance in the coronary circulation would only arise in parallel with other elements of the RLC system. Indeed, the nature of this e ect in the physiological system enforces this view: flow through the coronary vasculature has the option of inflating the vessels or simply flowing through. The two options are clearly in parallel, in the sense that they can be independent of each other. Nevertheless, in this section we examine the capacitance e ect in combination with resistance, both in series and in parallel, in order to compare the two cases.
Consider resistance R and capacitance C in series at first, where the complex impedance, from Eqs. 4.9.34, 36, is given by
Z = R + |
1 |
|
(6.6.1) |
iωC |
|||
= R − |
i |
(6.6.2) |
|
|
|
||
ωC |
|||
where ω is the angular frequency. As in the previous section, for the individual harmonics of a composite wave, since they have di erent frequencies, we write
Zn = R − |
i |
(6.6.3) |
|
|
|
||
ωnC |
|||
ωn = 2πn |
n = 1, 2, . . . , N |
(6.6.4) |
|
where N is the number of harmonics. The real and imaginary parts of the complex impedance are given by, using subscripts r, i to denote real and imaginary as before,
znr = |
R |
(6.6.5) |
|
zni = |
|
−1 |
(6.6.6) |
|
ωnC |
||
|
|
|
|
We see again that the real part of the impedance represents pure resistance while the imaginary part in the present case represents the capacitance e ects.
Following the same steps as in the previous section, we find the real parts of individual harmonics of the flow wave
