The Physics of Coronory Blood Flow - M. Zamir

108 3 Basic Lumped Elements

qC (t) = C d(Δp)

dt

=eat {A(− cos(bt) − 2btC sin(bt)) 2R

where K is a constant of integration. As before, using the condition of constant flow rate under the present scenario, namely qR(t) + qL(t) + qC (t) =

q(constant), we find, after some algebra,

The flow rates in Eqs. 3.8.36–38 can now be put in the following nondimensional form

We note that the condition of constant flow rate into the system required under the present scenario, which in nondimensional form reads

is satified at time t = 0 and at all other times.

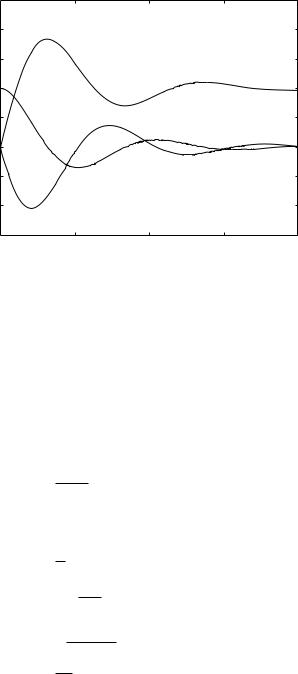
As before, only values of the time constants are required now to complete the solution. Results using tL = 1.0, tC = 2.5 are shown in Fig. 3.8.2. At time t = 0 the inductive and capacitive flow rates are zero as prescribed, while the resistive flow rate, as a consequence, has the value 1.0. As in the case of tL = 1.0, tC = 0.1 (Fig. 3.8.1), initially all flow is going through the resistive tube, but fairly soon thereafter this flow diminishes while the inductive flow grows to encompass total flow into the system. The di erence between the two cases, however, is that in the present case the process is accompanied by oscillations which are usually associated with “underdamping”, while the behaviour observed in the previous case (Fig. 3.8.1) is associated with “overdamping”. Since the inertial time constant is the same in both cases, namely tL = 1.0, this di erent behaviour is due entirely to the di erence in the values of the capacitive time constant tC (= CR). Assuming, for the purpose of comparison, that the value of C is the same in the two cases, then the value of R in the present case where tC = 2.5 is 25 times larger than the value of R in the previous case where tC = 0.1. Thus, the underdamped dynamics observed in Fig. 3.8.2 is here associated with a higher value of the resistance R, which is the reverse of what occurs when the R, L, C elements are in series. The reason for this is that in this section we are dealing with a parallel LRC system and under a condition of constant flow rate into the system. Under these circumstances, a lower value of the resistance R diverts more flow into the resistance tube which has a more stabilizing e ect on the dynamics of the system, while higher values of R have the opposite e ect. By contrast, when the LRC system is in series, lower values of R lead to an increase of flow to all components of the system, which has a destabilizing e ect, while higher values of R have a damping and hence a stabilizing e ect.

If 4tC = tL, finally, then Eq. 3.8.2 has two identical real roots given by

Fig. 3.8.2. Flow rates qR, qL, qC in an LRC system in parallel under a condition of constant flow, as in Fig. 3.8.1, but results here are based on tL = 1.0, tC = 2.5 (compared with tL = 1.0, tC = 2.5 in Fig. 3.8.1). While the ultimate outcome is the same in both cases, the oscillations in this figure are indicative of what is usually referred to as an “underdamped” system, while their absence in Fig. 3.8.1 is indicative of an “overdamped” system. Since the higher value of tC in the present case is associated with a higher value of R, these results show that in the parallel LRC system higher values of the resistance have a destabilizing e ect, in contrast with the LRC system in series where the reverse is true (see text).

Using this result for Δp in Eqs. 3.8.7–9, we find

qR(t) = Δp(t) R

1

qL(t) = L Δp(t)dt

qC (t) = C d(Δp(t))

dt

where K is a constant of integration. As before, using the condition of constant flow rate under the present scenario, namely qR(t) + qL(t) + qC (t) =

q(constant), we find, after some algebra,

The flow rates in Eqs. 3.8.55–57 can now be put in the following nondimensional form

We note that the condition of a constant flow rate into the system required under the present scenario, namely qR(t) + qL(t) + qC (t) = 1, is satified at time t = 0 and at all other times. As before, only values of the inertial and

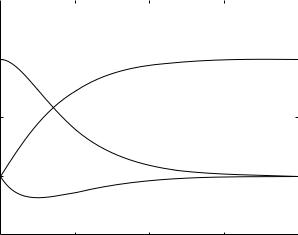
Fig. 3.8.3. Flow rates qR, qL, qC in an LRC system in parallel under a condition of constant flow, as in Fig. 3.8.1,2, but results here are based on tL = 1.0, tC = 0.25 (hence 4tC = tL). While the ultimate outcome is the same in all three cases, the present case represents a singular case of “critical damping” which occurs with only this particular ratio of the time constants (see text).

capacitive time constants are required now to complete the solution. Results using tL = 1.0, tC = 0.25 (hence 4tC = tL) are shown in Fig. 3.8.3. Dynamics of the system observed in this figure indicate what is usually referred to as “critical damping”, which is a singular condition between the overdamped and the underdamped conditions. With tL = 1.0, only a single value of tC produces critically damped dynamics, while a range of values can produce overdamped or underdamped dynamics.

3.9 Summary

A lumped model of the coronary circulation must at a minimum include the three basic elements of resistance, inductance, and capacitance, because that circulation, being a fluid flow system, involves the movement of a fluid that has mass and is therefore associated with inductance when accelerated or decelerated; the moving fluid is viscous and is therefore subject to resistance resulting from the no-slip boundary condition at vessel walls; and the vessels are elastic, thus allowing changes in volume and hence producing capacitance e ects. While the location and arrangement of these elements cannot be determined directly from the physiological system, the lumped model concept is based on the prospect that they can be determined indirectly, by modelling.

The RLC system in series, though clearly not an appropriate model of the physiological system, provides an important starting point and a useful reference.

Free dynamics of the RLC system represent basic intrinsic characteristics of the system which ultimately determine how it responds to external forces. The results are relevant to the dynamics of the coronary circulation to the extent that they demonstrate clearly how any change in the relative values of R, L, C, that may occur as a result of disease or clinical intervention, may change the intrinsic characteristics of the system and hence its dynamic behaviour.

Flow in two parallel resistive tubes may be examined under two di erent conditions: constant pressure drop across the two tubes, or constant total flow rate through the system. The second of these is of particular interest in the physiological system because of regulatory mechanisms that respond to local oxygen consumption by cardiac tissue, which is related to flow rate rather than pressure. Under constant pressure, a change in the resistance of one tube will change the flow rate in that tube but not in the other. Under constant flow rate, a change in the resistance of one tube will a ect the flow rate in both tubes.

Flow through a resistive and an inductive tube in parallel produce results that are physiologically unrealistic under the scenario of constant pressure drop as well as that of constant flow rate. Inductive flow rate in one case becomes infinite and in the other it becomes equal to total flow rate through the system. The reason for this, of course, is that under the present parallel arrangement the inductive tube is in isolation in the sense that flow has the option of taking the inductive route without passing through the resistance. The situation is somewhat artificial because while the inductive e ect due to fluid inertia certainly exists in the physiological system, it does not exist in isolation. We have seen in earlier sections that when fluid in a tube is accelerated from rest, the inertial e ect is normally tied in series with resistance due to the viscous e ect at the tube wall. Thus, one is led to conclude that in the normal physiological setting inductive flow is always in series with some other elements of the system, not in parallel. However, under pathological conditions, specifically an injury, a breach in the vascular system through which blood can escape, a parallel inductive route is created as depicted in the present model.

For flow through a resistor and a capacitor in parallel, under the constant pressure drop scenario there is no interaction between the resistive and capacitive flows, but under the scenario of constant flow rate the pressure drop driving the two parallel flows changes as time goes on and the two flows change with it. Since total flow rate must remain constant as prescribed under this scenario, changes in the two parallel flows must occur in a complimentary way, a change in one a ecting the other. From a prescribed condition of the two parallel flows being equal to each other initially, as time goes on the system moves towards an ultimate condition of zero capacitive flow and resistive flow

114 3 Basic Lumped Elements

equal to total flow. Thus, while inductive flow in parallel grows, as was found in the previous section, capacitive flow in parallel diminishes ultimately to zero.

Under a condition of constant pressure drop the RLC system in parallel behaves as if the capacitor C does not exist, that is, it behaves as an RL system in parallel under constant pressure drop.

Under a condition of constant flow rate, we note first the important difference between the dynamics of the series and parallel LRC systems, namely that in the series system the resistance R has a damping e ect while in the parallel system it has a destabilizing e ect. In the series system, overdamped dynamics occur at higher values of the resistance R, and underdamped dynamics occur at lower values of R. In the parallel system the reverse is true.

Second, in the parallel LRC system, under constant flow conditions, the inductive flow ultimately encompasses the entire flow into the system, thus reducing resistive and capacitive flow to zero. This occurs at all three dynamic modes of the system, namely the overdamped, underdamped, and the critically damped modes.

Finally, while inductance is an important factor in the normal dynamics of the coronary circulation and in the cardiovascular system in general, as it occurs whenever fluid is being accelerated or decelerated, it is usually present in series with the resistance and capacitance rather than in parallel. Parallel reactance routes are not normally present in the coronary circulation or in the cardiovascular system in general, since they would ultimately “steal” the entire flow away from other elements of the system. Under abnormal circumstances, however, as in the presence of a breach in the vascular system through which blood can escape freely, the new route for blood flow will act precisely as a inductive route. Fluid will be accelerated freely through the breach until it ultimately steals the entire flow rate available, away from all other routes within the system, precisely as seen in Figs.3.8.1-3. This leads to failure of the organ or organism if the breach is not stopped. While the ultimate cause of this failure is metabolic, in the sense that tissue is being deprived from its metabolic needs, it is important to note that the primary cause of the failure is related to the dynamics of the system.

4

Forced Dynamics of the RLC System

4.1 Introduction

In the previous chapter we examined some basic dynamics of the R, L, C elements, first arranged in series under a condition of zero driving pressure drop (“free” dynamics), and then in parallel under a condition of either constant flow rate into the system or constant driving pressure drop. While these scenarios are somewhat artificial, they illustrate some intrinsic characteristics of the RLC system and highlight important di erences between the dynamics of the series and parallel arrangement of the system.

The dynamics of the coronary circulation are neither “free” nor driven by constant pressure or constant flow rate. They are “forced” dynamics, driven by the same pressure wave that drives blood flow in the systemic circulation, namely the pulsatile pressure wave generated by the pumping action of the left ventricle, the so-called “cardiac pressure wave”. In order to bring the dynamics of the RLC system of the previous chapter closer to the dynamics of the coronary circulation, therefore, it is necessary to give the driving pressure drop Δp the form of the cardiac pressure wave.

In free dynamics, the behaviour of the RLC system is determined by the characteristics of the system only, namely the series or parallel arrangement of the R, L, C elements relative to each other, and their relative values. In forced dynamics, the behaviour of the system is determined by these same factors but also by the form of the driving pressure, that is, by the form of Δp as a function of time. We shall see later that the cardiac pressure waveform is a “composite” function of time consisting of an assortment of simple sine and cosine waves which are referred to as its “harmonics”, as discussed in Chapter 5. In the present chapter, as a first step, therefore, we examine the dynamics of the RLC system under a driving pressure drop that consists of a single harmonic, a simple sine or cosine function, to focus on the response of the system to a simple periodic driving force. In Chapter 6 we consider the dynamics of the system under the force of the full composite form of the cardiac pressure wave.

116 4 Forced Dynamics of the RLC System

4.2 The Particular Solution

We begin with the RLC system in series illustrated schematically in Fig. 3.2.3 and governed by Eq. 3.2.4. Taking the driving pressure drop in that equation as a simple cosine function, namely

where Δp0 is a constant and ω is the frequency of oscillation of the cosine function. With this form of Δp Eq. 3.2.4 becomes

As before, for the purpose of solving this equation it is convenient to di erentiate it once in order to eliminate the integral term, to get

The solution of this equation consists of two parts, usually referred to as the “homogeneous” part, to be denoted by qh(t), and the “particular” part, to be denoted by qp(t). The total solution is given by the sum of these two parts, that is,

The homogeneous part of the solution is, by definition, the general solution of the homogeneous form of Eq. 4.2.3, that is, it satisfies

This equation is identical with Eq. 3.3.1 whose solutions were obtained fully in Section 3.3. Thus qh(t) represents the flow rate obtained in the free dynamics scenarios considered in Section 3.3, and the solutions of Eq. 4.2.5 can be taken directly from that section.

The particular part of the solution, or the particular solution, represents any particular solution (not containing arbitrary constants) of Eq. 4.2.3, that is any particular solution of

In the theory of di erential equations [116] it has been found that the form of a particular solution of this equation depends on the functional form of the term on the right hand side of the equation. Specifically, when the term on the right-hand side is a simple sine or cosine function, as it is in this case, a particular solution is of the form

where Kc, Ks are constants to be determined by the equation itself, as shown below, and are not to be confused with the arbitrary constants A, B in the general solution of Eq. 4.2.5 which are determined by the initial flow conditions as will be shown in the next section, and as was done in Section 3.3. The constants Kc, Ks here are determined simply by substituting for qp(t) and its derivatives from Eq. 4.2.7 into Eq. 4.2.6 to get

L(−Kcω2 cos ωt − Ksω2 sin ωt) + R(−Kcω sin ωt + Bω cos ωt)

Equating terms in sin ωt and cos ωt on both sides of this equation, we find

These are two equations in the two unknown constants Kc, Ks. Their solution is standard, though involving some tedious algegra, giving

Inserting these values of the constants in Eq. 4.2.7, we obtain, finally, the particular solution as

4.3 Using the Complex Exponential Function

Results obtained in the previous section can be obtained more elegantly and more easily by considering a driving pressure drop Δp in the form of a complex function rather than a simple sine or cosine function. Thus, instead of the cosine function in Eq. 4.2.1, we now write

where Δp0 is a constant as before, and the other element on the right is the well known complex exponential function