Методичка по инж.графике в помощь

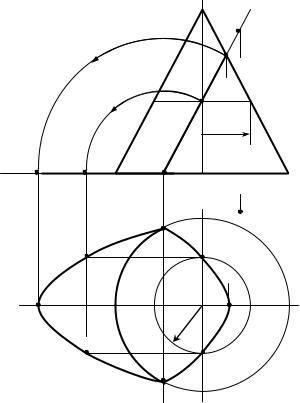
Задача: способом вращения вокруг горизонтального следа плоскоти РП1, определить натуральную величину сечения прямого кругового конуса, фронтально-проецирующей плоскостью Р, проходящей через точку М, параллельно контурной образующей SA. Определить видимость линий

(рис.130).

Вершина параболы расположена на контурной образующей конуса, а точки лежащие на основании ветвей параболы, расположены на основании конуса.

Две промежуточные точки, не обозначенные на чертеже, строятся для выяснения окончательного характера линии пересечения. Расположены они на окружности конуса радиуса R.

2.Натуральная величина (Н.В.) сечения (2111131) определяется способом вращения плоскости Р с горизонтальной плоскостью проекций.

3.Определяется видимость линий (все, что расположено над секущей плоскостью, будет видимо).

70

Пересечение цилиндра вращения плоскостью

При пересечении такого цилиндра плоскостью образуются линии:

Задача: построить линию пересечения поверхности цилиндра вращения плоскостью треугольника АВС . Определить видимость линий (рис.135).

проекцию линии пересечения - эллипс. 4. Определяем видимость линий.

С1

Рис. 135. Пересечение цилиндра плоскостью треугольника АВС

72

Пересечение сферы плоскостью

При пересечении сферы плоскостью в сечении получается окружность, которая может проецироваться в зависимости от положения секущей плоскостью относительно плоскости проекций, в виде окружности, эллипса или отрезка прямой линии.

Задача: построить линию пересечения поверхности сферы горизонтально проецирующей плоскостью Р, заданной горизонтальным следом РП1. Определить видимость линий (рис. 136).

Рис. 136. Построение линии пересечения сферы горизонтально проецирующей плоскостью

.

73

Пересечение тора (кольца) плоскостью

На рис.137 показаны сечения поверхности открытого тора.

1.В первом случае тор пересекается плоскостью, проходящей через ось тора (l=0, где l расстояние секущей плоскости от этой оси), по двум окружностям.

В других случаях по кривым, в зависимости от l, R и r. Эти кривые называются кривыми Персея. Это алгебраические кривые четвертого порядка.

2.l < R-r - овал с одной осью симметрии

3.l=R-r - двухлепестковая кривая, с узловой точкой в начале координат

4.l>R-r - волнообразная кривая

5.l≥R - овал с двумя осями симметрии

Тор имеет две системы круговых сечений, расположенных в плоскостях перпендикулярных к оси вращения и проходящих через ось вращения.

Рис. 137а. Пересечение открытого тора фронтально-проецирующей плоскостью Р

74

Пересечение прямой линии с поверхностью

Прямая пересекает поверхность в двух точках. Построение этих точек может быть частным или общим. Когда заданная поверхность проецирующая, то эти точки определяются без вспомогательных построений, т.к. одна из проекций точек пересечения будет находиться в точках пересечения прямой со следом поверхности.

В общем случае точки пересечения отыскиваются по аналогии с построением точки пересечения прямой с плоскостью, т.е. выполняются следующие действия:

1.Прямая заключается во вспомогательную секущую плоскость.

2.Строится линия пересечения поверхности этой плоскостью.

3.Определяются точки пересечения прямой с линией пересечения. Это будут искомые точки.

Вспомогательные секущие плоскости выбираются так, чтобы они пересекали поверхности по прямым линиям или окружностям.

Частные случаи решения задач

Задача: построить точки пересечения прямой АВ с заданными поверхностями. Определить видимость линий (рис.138).

Рис.138. Пересечение прямой с проецирующими поверхностями

75

Решение Так как заданные поверхности прямого кругового цилиндра и прямой

трехгранной призмы являются горизонтальнопроецирующими, то горизонтальные проекции точек пересечения прямой АВ M1 и N1 находятся в точках пересечения горизонтальной проекции прямой А1В1 с горизонтальными следами поверхностей.

Фронтальные проекции точек пересечения M2 и N2 находятся на пересечении линий проекционной связи, проведенных из точек M1, N1 с фронтальной проекцией прямой А2В2.

Затем определяется видимость линий.

Общие случаи решения задач Задача: построить точки пересечения горизонтальной прямой АВ с

поверхностями сферы и конуса вращения. Определить видимость линий (рис. 139).

Рис. 139. Построение точек пересечения прямой с поверхностями сферы и конуса вращения

Решение При решении этой задачи выполняются специальные построения.

1.Горизонтальная прямая АВ заключается в горизонтальные плоскости Р,

заданные на чертеже своим фронтальным следом РП2, которые проходят через фронтальные проекции прямой А2В2.

2.Плоскость Р пересекает сферу и конус по окружностям радиуса R (на чертеже радиус изображен проекциями R1 и R2).

3.На горизонтальных проекциях эти окружности пересекаются с

горизонтальными проекциями прямой А1В1 в точках M1, N1, которые являются горизонтальными проекциями точек пересечения прямой с поверхностями.

4.С помощью линий проекционной связи определяются фронтальные проекции точек пересечения M2, N2.

76

5. Определяется видимость линий. Примечание

Когда поверхность сферы пересекается прямой общего положения, то для упрощения решения задачи необходимо воспользоваться одним из способов преобразования чертежа, с условием, что прямая общего положения после преобразования чертежа стала бы горизонтальной или фронтальной. Лучше использовать способ замены плоскости проекций.

После преобразования решение задачи сведется к решению вышеуказанной задачи.

Задача: способом плоскопараллельного перемещения определить натуральную величину расстояния между точками пересечения прямой MN с поверхностью наклонной призмы с основанием АВС (рис.140).

32 РП2

Горизонтальная проекция линии пересечения строится с помощью горизонтальных проекций точек линии пересечения ребер поверхности 11,21,31. Соединив эти точки прямыми линиями, получим горизонтальную проекцию линии пересечения – треугольник 112131.

3.Там, где горизонтальная проекция прямой M1N1 пересекает горизонтальную проекцию треугольника 112131, содержатся горизонтальные проекции точек линии пересечения К1, L1. С помощью линий проекционной связи строим фронтальные проекции точек линии пересечения K2, L2. Определяем видимость линий.

4.Способом плоскопараллельного перемещения определяем натуральную величину расстояния между точками пересечения. Для этого K11L11, равное

77

K1L1 располагаем параллельно оси проекций Х. Строим фронтальную проекцию этого расстояния (К12L12), которое и будет являться натуральной величиной расстояния между точками пересечения.

Задача: заменой плоскостей проекций определить натуральную величину расстояния между точками пересечения прямой MN с поверхностью трехгранной пирамиды SABC. Определить видимость линий (рис.141).

Решение

1.Прямую MN заключаем во фронтально-проецирующую плоскость Р (на чертеже плоскость задана своим следом PП2).

2.Строим линию пересечения пирамиды этой плоскостью. В сечении образуется треугольник (на чертеже он изображен своими проекциями: 122232, 112131).

3.Горизонтальная проекция треугольника 112131 пересекается с горизонтальной проекцией прямой M1N1 в точках K1 и L1. Эти точки будут горизонтальными проекциями точек пересечения прямой с пирамидой. Затем строятся фронтальные проекции точек пересечения K2 и L2.

4.Определяется видимость прямой MN.

Способом замены фронтальной плоскости проекций П2 на новую П3

определяем натуральную величину расстояния между точками пересечения заданной прямой K3L3.

78