
Методичка по инж.графике в помощь
.pdf
Плоскость
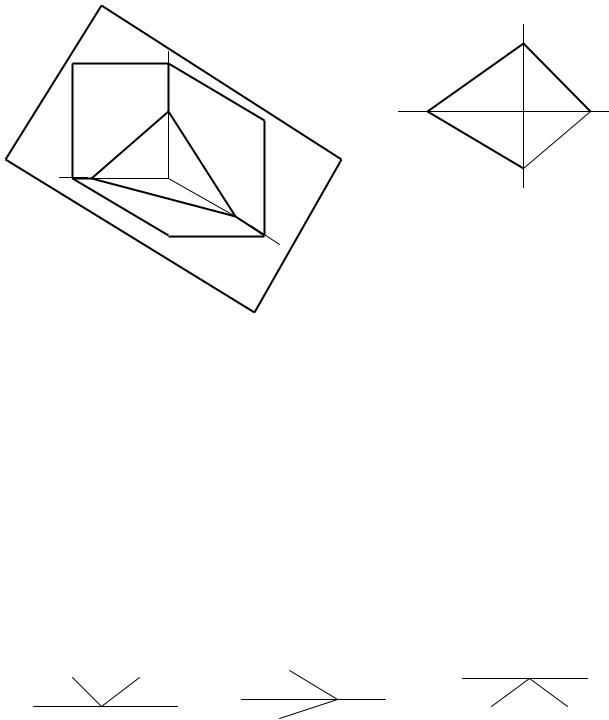
Плоскостью называется непрерывное множество последовательных положений образующей прямой линии, перемещающейся параллельно самой себе по направляющей прямой линии (рис.38).
С2
С1 |
В |
AB – направляющая |
С |
|
CD – образующая |
|
|
|
|
|
D2 |
A |
D1 |
СD || C1D1 || C2D2 |
|
D |
|
Рис.38. Образование плоскости
Задание плоскости
Положение плоскости в пространстве определяется:
a)тремя точками, не лежащими на одной прямой,
b)прямой и точкой, взятой вне прямой,
c)двумя пересекающимися прямыми,
d)двумя параллельными прямыми
e)отсеком или куском плоскости,
f)следами плоскости.
На чертеже плоскость задается проекциями элементов, определяющих плоскость в пространстве.
|
А2 |
В2 С2 |
|
|
D2 |
E2 |
|
L2 |
|
|
|
Q2 |
R2 |
|
F2 |
PП2 |
|
|
|
|
C2 |
|
|
|
K2 |
N2 P2 |
S2 |
|
|
G2 |
РХ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
Х |
|
X |
|
|
X |
|
X |
|
|
X |
|||||||
|
А1 |
|
|
C1 |
|
|
|
K1 |
|
P1 |
S1 |
|
|
G1 |
PП1 |
||
|
С1 |
|
|
E1 |
|
|
N1 |
|
|
|
H1 |
|
|||||
|
|
В1 |
|
|
D1 |
|
|
L1 |
|
|
|
Q1 |
R1 |
|
F1 |
|
|
|
|
(a) |
|
|
(b) |
|
|
(c) |
|
|
|
(d) |
|
|
(e) |
(f) |
|
20
Следы плоскости
Линии пересечения плоскости с плоскостями проекций называются следами плоскости (рис.39).
Р |
|
|
|
Z |
|
Z |
|
|
PZ |
|
|
|
|
|
PП2 |
|
|
|
П2 |
|
PX |
|
РП3 |
|
Pz |
|
O |
PY |
|
PП2 |
П3 |
X |
|
Y |
|
|
|
PП1 |
|
||
РХ |
РП3 |
|
|
|
|
Х |
O |
|
|
Y |
|
|
PП1 |
PY |
Рис.40. Чертеж плоскости общего по- |
||
|
П1 |
|
ложения, заданной следами |
|
|
|
Y |
– горизонтальный след |
|
PП1 |
|
|
PП2 |
– фронтальный след |
|
РП3 |
– профильный след |
Рис.39. Следы плоскости |
PX, PY, PZ – точки схода следов |
|
Каждый из следов плоскости есть линия плоскости, лежащая в плоскости проекций, т.е. фактически следы – это пересекающиеся прямые плоскости.
Горизонтальная проекция горизонтального следа плоскости совпадает с горизонтальным следом, а фронтальная его проекция находится на оси проекций. Фронтальная проекция фронтального следа плоскости совпадает с фронтальным следом, а горизонтальная его проекция находится на оси проекций.
Следует заметить, что разноименные проекции каждого следа на чертеже не обозначаются, т.к. они лежат на оси проекций.
Обычно плоскость задают двумя следами, горизонтальным и фронтальным, но, если есть необходимость, то профильный след всегда можно построить.
На чертеже, указанном выше, показаны следы плоскости Р (PП1, PП2) в первой четверти. Но они могут продолжаться в любом направлении. Например, плоскость Р, заданная своими следами в первой четверти, может быть задана в других четвертях так:
РП1 Рх РП2 |
|
РП1 |
|
РХ |
Х |
РХ |
Х РП2 |
РП1 |
|
Х |
|
РП2 |
Четвертая четверть |
|
Вторая четверть |
Третья четверть |
|||
Если плоскость задана другими элементами, то всегда можно перейти к заданию ее следами.
21
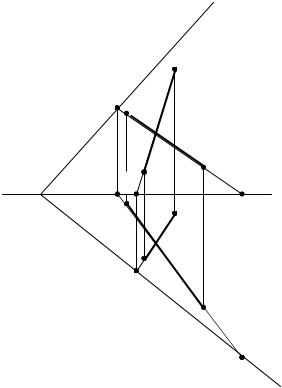
Задача: построить следы плоскости Р, заданной двумя пересекающимися прямыми AB и CD (рис.41).
|
|
PП2 |
D2 |
Решение |
|
|
N2 |
A2 |
1. Согласно правилу построения следов |
||
|
|
||||
|
|
|
|
|
отрезка прямой линии, строим горизон- |
|
|
|
|
|
тальный и фронтальный следы одной из |
|
|
|
|
|
|
|
|
|
C2 |
B2 |
прямых. В данном случае следы прямой |
PX |
N1 |
K2 |
|
M2 |
АВ (точки М1, М2 и N1, N2). |
X |
A1 |
|
D1 |
2. Строим один из следов другой пря- |
|
|
|
|
|
|
|
|
K1 C1 |
|
мой. |
||
|
|
В нашем случае горизонтальный след |
|||
|
|
PП1 |
B1 |
прямой CD (точка К1). |
|
|
|
|
|||
М1
Рис.41. Построение следов плоскости, заданной пересекающимися прямыми
3.Т.к. следы прямой, лежащей в плоскости, всегда лежат на одноименных следах плоскости, то соединяя горизонтальные проекции следов отрезков АВ и CD
(точки К1и М1) прямой линией, мы получим горизонтальный след плоскости РП1. Этот след пересекает ось проекций в точке РХ – точки схода следов.
4.Проведя из точки РХ прямую через фронтальный след прямой АВ (точку N2), мы получим фронтальный след искомой плоскости РП2.
Так мы осуществили переход от плоскости, заданной двумя пересекающимися прямыми, к плоскости, которая выражена ее следами.
22

Определение натуральной длины отрезка прямой линии и углов его наклона к плоскостям проекций
А
С  α В
α В
 ВР АР Р
ВР АР Р
Рис.42. Построение натуральной длины отрезка прямой линии и углов его наклона к плоскостям проекций
Выполним построение проекции отрезка прямой линии АВ на плоскость Р. Получим его проекцию АРВР
(рис.42).
Из точки В проведем прямую ВС || АРВР. Получим прямоугольный треугольник АВС, в котором гипотенуза АВ есть натуральная величина отрезка, а угол α - угол наклона отрезка АВ к плоскости Р.
Рассматривая этот треугольник, делаем два вывода:
1.Натуральная величина отрезка прямой линии есть гипотенуза прямоугольного треугольника, у которого один катет равен проекции отрезка на
данную плоскость (ВС = АРВР), а второй – есть разность расстояний концов отрезка до данной плоскости (АС=ААР-ВВР).
2.Угол наклона отрезка прямой линии к плоскости проекции определяется как угол составленный отрезком прямой и его проекцией на данную плос-
кость (угол α).
Этот способ определения натуральной величины отрезка и угла его наклона к плоскости называется «способом прямоугольного треугольника».
Задача: определить натуральную величину отрезка прямой АВ и угол его наклона к горизонтальной плоскости проекций (рис.43). Отрезок задан своими координатами А(40,5,25), В(7,10,10).
А2 |
|
|
1. Строим проекции отрезка АВ по за- |
||
= |
|
|
данным координатам. |
||
|
|
|
|
2.Строим |
прямоугольный треугольник |
С |
|
В2 |
(согласно правилу) А1В1В0, берем за один |
||
Х |
|
О |
катет горизонтальную проекцию отрезка |
||
А1 |
|
|
А1В1. |
|
|
|
α |
|
В1 |
2.1. Из точи В1 проводим перпендику- |
|
|
|
= |
ляр В1К, |
на котором откладываем вели- |
|
|
|
|
|
чину второго катета В1В0, равного разно- |
|
|
К |
|
В0 |
сти расстояний концов отрезка АВ до го- |
|
Рис.43. Определить натуральную величи- |
ризонтальной плоскости проекций (В1В0 |
||||
ну отрезка прямой и угол его наклона к |
|
|
|||
горизонтальной плоскости проекций |
= А2С). |
|
2.2. Соединяем точки А1 и В0, получим гипотенузу прямоугольного треугольника А1В0. Это будет натуральная величина отрезка АВ.
3. Угол наклона отрезка АВ к горизонтальной плоскости проекции будет равен углу α, как угол, составленный самой прямой и его проекцией на горизонтальную плоскость.
23

Положение плоскости относительно плоскостей проекций
Плоскость может занимать семь различных положений относительно плоскостей проекций, из них одно общее и шесть частных.
Плоскость общего положения
Плоскость, не перпендикулярная ни к одной из плоскостей проекций, называется плоскостью общего положения (рис.44).
Такая плоскость имеет три следа и пересекает каждую из осей проекций. Следы этой плоскости не перпендикулярны к осям проекций. Плоскость общего положения наклонена к плоскостям проекций под некоторыми углами, исключая угол в 90О. Для определения натуральной величины этих углов необходимо выполнить специальные построения.
1. Плоскость задана следами.
|
|
|
|
П2 |
РП2 |
|
|
|
|
|
РХ |
||
|
|
РП2 |
||||
|
РХ |
Р |
Х |
|||
|
Х |
|
РП1 |
|
|
РП1 |
|
|
|
||||
|
|
|
|
|
П1 |
|
Рис.44. Следы плоскости общего по- |
Рис.45. Чертеж плоскости общего по- |
|||||
|
|
|
ложения |
ложения, заданной следами. |
||
|
|
|
|
|||
2.Плоскость общего положения, заданная другими элементами (например, треугольником).
Вэтом случае ни одна из проекций плоскости не будет выглядеть прямой линией.
В2
А2 С2
ОНи горизонтальная проекция треугольника
Х |
А1В1С1, ни фронтальная проекция А2В2С2, не |
В1 |
равны натуральной величине треугольника |
А1 |
АВС. |
С1 |
|
Рис.46. Чертеж плоскости общего |
|
положения, заданной треугольником |
|
24

Плоскости частного положения
Плоскости, перпендикулярные одной или двум плоскостям проекций, называются плоскостями частного положения.
1. Проецирующие плоскости
Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими, т.к. они содержат все проецирующие лучи относительно данной плоскости проекции.
Такие плоскости всегда имеют один «собирательный» след, т.е. след, который содержит проекции всех точек, линий, фигур, лежащих в этих плоскостях.
Другие следы обязательно перпендикулярны осям проекций.
Если проецирующие плоскости заданы другими элементами, то на чертеже одна из проекций всегда будет выглядеть в виде отрезка прямой линии, не параллельной оси проекций. Эта проекция и будет являться следом такой плоскости.
а) горизонтально-проецирующая плоскость – плоскость, перпендику-
лярная горизонтальной плоскости проекций.
• Горизонтально-проецирующая плоскость задана следами (Р П1) (рис.47).
РП2 |
А2 |
П2 |
РП2 |
||
|
Р |
|
|
|
А2 |
РХ |
А |
|
|
|
|
|
|
|
РХ |
||
Х |
|
|
|
|
|
А1 |
|
|
|
Х |
|
|
|
|
|
||
|
РП1 |
|
|
П1 |
β |
|
|
|
|
А1 |
|
|
|
|
|
|
РП1 |
Рис.47. Горизонтально-проецирующая плос- |
Рис.48. Чертеж горизонтально-проеци- |
||||
|
кость Р, |
заданная следами |
рующей плоскости Р, заданной следами |
||
РП2 – фронтальный след перпендикулярен оси проекций (РП2 Х) – признак горизонтально проецирующей плоскости.
РП1 – горизонтальный след (собирательный). Точка А, лежащая в плоскости, имеет свою горизонтальную проекцию А1 на горизонтальном следе.
β - угол наклона плоскости Р к фронтальной плоскости проекций.
25
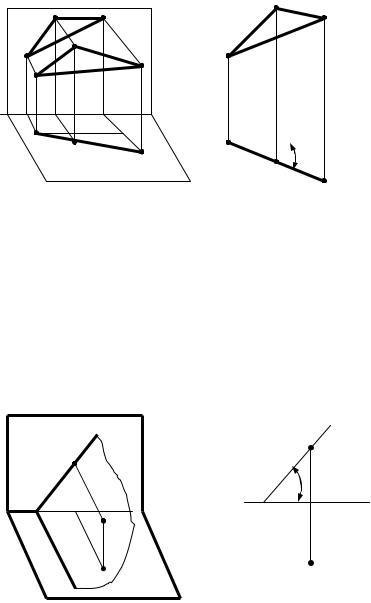
•Горизонтально-проецирующая плоскость задана треугольником АВС (АВС
_|_ П1) (рис.49).
В2 |
С2 П2 |
В
А2 С
А
Х
А1 В1
С1 П1
Рис.49. Горизонтальнопроецирующая плоскость, задана треугольником
В2 С2
Горизонтальная проекция
А2 треугольника А1В1С1 – прямая линия (признак
Огоризонтально-проеци-
Х |
|
|
|
|
|
|
рующей плоскости). |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
β - угол наклона треу- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гольника к фронтальной |
|
А1 |
β |
|
|
||||
|
|
|
В1 |
|
|
плоскости проекций. |
|
|
|
|
|
|
С1 |
||
Рис.50. Чертеж горизонтальнопроецирующей плоскости, заданной треугольником
б) фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Р _|_ П2).
• Фронтально-проецирующая плоскость задана следами (рис.51).
|
|
|
|
П2 |
|
|
|
|
|
|
Горизонтальный |
след |
|
|
|
А2 Р |
|
|
|
РП2 |
А2 |
плоскости П1 перпенди- |
|||||
|
РП2 |
|
|
|
|
|
|
|
|
|
кулярен оси проекций |
||
|
|
|
|
|
|
|
|||||||
|
РХ |
|
|
|
|
РХ |
|
α |
|
О |
(РП1 _|_ X) – признак |
||
|
|
|
|
|
|
||||||||
Х |
|
|
|
|
|
|
Х |
|
|
|
|
фронтально-проецирую- |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
А |
|
|
|
|
|
|
щей плоскости. |
|
|
|
РП1 |
|
РП1 |
|
А1 |
|
|
РП2 – фронтальный след |
|||||
|
|
|
|
А1 |
П1 |
|
|
|
|
|
(собирательный). |
|
|
|
Рис.51. Фронтально- |
Рис.52. Чертеж фронтально- |
|
|
|||||||||
проецирующая плоскость |
проецирующей плоскости, |
|
|
||||||||||
|
задана следами |
|
заданной следами |
|
|
||||||||
Точка А, лежащая в этой плоскости, имеет свою фронтальную проекцию А2, лежащую на фронтальном следе плоскости РП2.
α - угол наклона плоскости Р к горизонтальной плоскости проекций.
26

• Фронтально-проецирующая плоскость задана треугольником АВС (АВС _|_ П2) (рис.53).
С2 П2 В2 С
А2
АВ
Х
А1 С1 В1
Рис.53. Фронтальнопроецирующая плоскость задана треугольником
|
|
|
|
С2 |
А2В2С2 – фронтальная |
||||
|
|
|
В2 |
||||||
|
|
|
|
|
|
|
проекция |
треугольника |
|
|
А2 |
α |
АВС – прямая |
линия |
|||||
|
|
|
|
|
|
|
(признак |
фронтально- |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
О |
прецирующей |
плоско- |
||
|
|
|
|
|
|
|
сти). |
|
|
Х |
|
|
|
|
|
|
|||
А1 |
|
|
|
|
α - угол наклона тре- |
||||
|
С1 |
угольника АВС к гори- |
|||||||
|
|
|
|
|
|
|
зонтальной |
плоскости |
|
|
|
|
|
В1 |
проекций. |
|
|
||
Рис.54. Чертеж фронтальнопроецирующей плоскости, заданной треугольником
в) профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
• Профильно-проецирующая плоскость задана следами (Р_|_ П3) (рис.55).
|
РП2 |
П2 |
|
|
РП2 |
РZ |
|
|
Р А2 |
AZ |
|
П3 |
|
РП3 |
|
|
|
А |
А3 |
РП3 |
А2 |
AZ |
А3 |
|
|
Х AX |
|
AY PY |
|||
|
|
AX |
|
|
|
||
Х |
|
О |
|
|
|
|
|
|
А1 |
|
А1 |
AY |
|
||
|
|
|
|
|
|||
|
|
AY |
|
|
|||
|
|
|
|
|
|||
|
|
РП1 |
|
|
|
||
|
|
|
П1 |
РП1 |
|
PY |
|
|
|
|
|
|
|
||
Рис.55. Профильно-проецирующая |
Рис.56. Чертеж профильно-проецирующей плоско- |
плоскость задана следами |
сти, заданной следами |
Горизонтальный и фронтальные следы плоскости распложены параллельно оси проекций (РП1, РП2 || X) – признак профильно-проецирующей плоскости. Профильный след РП3 – собирательный.
Точка А, лежащая в плоскости, имеет свою профильную проекцию А3 на профильном следе РП3.
27
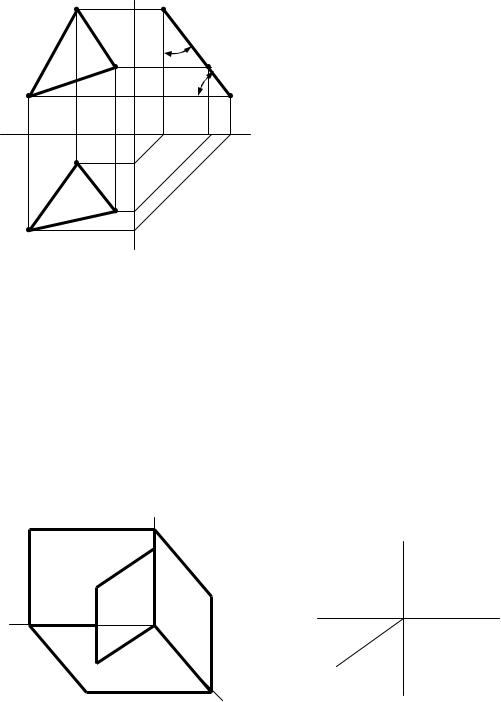
•Пофильно-проецирующая плоскость задана треугольником АВС (АВС _|_ П3) (рис.57).
А2 |
Z |
|
А3 |
|
β |
В2 |
В3 |
|
α |
С2 |
С3 |
|
O |
Х |
Y |
А1 |
|
В1 |
|
С1 |
Y |
|
|
Рис.57. Чертеж профильно-проецирующей |
|
плоскости, заданной треугольником |
|
Горизонтальная и фронтальная проекции треугольника АВС выглядят в виде
треугольников А1В1С1, А2В2С2. Профильная проекция треугольника вы-
глядит в виде отрезка прямой линии А3В3С3, которая наклонена под углом β к фронтальной плоскости проекций и под углом α к горизонтальной плоскости проекций.
Если пофильно-проецирующая плоскость задана в системе двух плоскостей проекций двумя своими проекциями (исключая задание следами), то нельзя сказать, что эта плоскость именно профильно-проецирующая. Это можно доказать только дополнительным построением.
Примечание: проецирующие плоскости, проходящие через оси проекций, называются осевыми.
Например:
•горизонтально-проецирующая осевая плоскость Р будет иметь фронтальный и профильный следы, совпадающие с осью Z (рис.58).
|
Z |
|
Z |
|
П2 |
РП2 |
РП3 |
|
РП2 РП3 |
||
|
|
|
|
Р |
П3 |
|
O≡PX |
Х |
О≡PX |
X |
Y |
|
РП1 |
РП1 |
|
|
П1 |
|
Y |
|
Y |
|
|
Рис.58. Горизонтально-проецирующая |
Рис.59. Чертеж горизонтально-проецирующей осе- |
||
осевая плоскость |
вой плоскости Р, заданной следами |
||
Если осевая плоскость делит двугранный угол пополам, то такая плоскость называется биссекторной, т.к. в ней находятся все биссектрисы этого угла и она содержит равноудаленные точки от плоскостей проекций.
28
2. Плоскости уровня
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня.
а) горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.
• Горизонтальная плоскость Р задана следами (Р || П1)(рис.60). |
|
||||||||
П2 |
Z |
|
|
|
Z |
|
|
|
|
|
PП2 |
|
|
|
Горизонтальная плос- |
||||
РП2 |
РZ |
РZ PП3 |
|
||||||
|
РП3 |
|
|
|
|
|
|
кость имеет два следа |
|
Р |
|
|
|
|
O |
|
– горизонтальный РП2 |
||
Х |
О |
|
|
X |
|
|
Y |
|| Х, и профильный РП3 |
|
|
|
|
|
|
|
|
|
|| Y. |
|
|
П1 |
|
|
|
Y |
|
(признак |
горизон- |
|
|
|
|
|
|
тальной |
плоскости, |
|||
Y |
Рис.61. Чертеж горизонтальной заданной следами) |
Рис.60. Горизонтальная плоскость |
плоскости Р, заданной следами |
• Горизонтальная плоскость задана треугольником АВС (АВС || П1) (рис.62).
|
А2 |
В2 |
С2 |
|
Фронтальная |
проекция треугольника |
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
О |
|
АВС выражена прямой линией А2В2С2, |
||||
Х |
|
|
|
|
|
параллельной оси Х (признак горизон- |
|||||
|
|
|
|
|
|
|
тальной плоскости). |
|
|
||
|
|
|
В1 |
|
|
|
|||||
|
|
|
|
|
Горизонтальная проекция треугольника |
||||||
|
А1 |
|
|
|
|
|
|
А1В1С1 равна натуральной величине тре- |
|||
|
|
|
С1 |
|
|
|
|
угольника АВС. (А1В1С1 = АВС) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рис.62. Горизонтальная плоскость задана |
|
|
|
|
|||||||
|
треугольником |
|
|
|
|
|
|
|
|
||
|
б) фронтальная плоскость – плоскость, параллельная фронтальной плос- |
||||||||||
кости проекций. |
|
|
|
|
|
|
|
|
|
||
|
• Фронтальная плоскость Р задана следами (Р || П2) (рис.63). |
|
|
||||||||
|
|
Z |
|
|
|
|
Z |
Фронтальная |
плоскость |
||
|
П2 |
|
|
|
|
|
РП3 |
Р имеет два следа. |
|
||
|
|
П3 |
|
|
|
|
|
Горизонтальный |
след |
||
|
|
|
|
Х |
О |
РY |
плоскости РП1 |
паралле- |
|||
|
|
О |
РП3 |
лен оси проекций Х (РП1 |
|||||||
Х |
Р |
|
|
|
|
РY |
|| Х). Это признак фрон- |
||||
|
|
|
|
РП1 |
|
тальной |
плоскости. |
||||
|
РП1 |
РY |
|
|
|
|
Y |
Профильный след |
пер- |
||
|
Y |
|
|
|
|
пендикулярен |
оси |
про- |
|||
|
|
|
|
Рис.64. Чертеж фронтальной |
екций Y (РП3_|_Y). |
|
|||||
Рис.63. Фронтальная плоскость Р |
плоскости Р, заданной своими |
|
|||||||||
|
|
|
|
|
|
|
|
следами |
|
|
|
29
