
Методичка по инж.графике в помощь
.pdf
Фронтальная проекция точки А2 будет перемещаться по следу плоскости вращения SП2, т.е. по прямой, параллельной оси проекций.
На чертеже (рис.93) это будет выглядеть так:
А22 А12 О2 А2
SП2
О12
Х
А21 |
О1≡О11 |
|
|
А1 |
|
|
||
А11
Рис.93. Чертеж вращения точки вокруг оси, перпендикулярной
к плоскости П1
ОО1 – ось вращения (ОО1 П1). SП2 – след плоскости вращения. О – центр вращения точки.
ОА – радиус вращения точки.
А1 – горизонтальная проекция т.А. А2 – фронтальная проекция т.А.
А11, А21 – новые положения горизонтальных проекций точки после вращения точки А вокруг оси вращения.
А12, А22 – новые положения фронтальных проекций точки после вращения точки А.
Вывод: при вращении точки вокруг оси, перпендикулярной плоскости проекций, одна из проекций точки все время перемещается по окружности, а другая - по прямой, параллельной оси проекций, т. е. по следу плоскости вращения.
Вращение отрезка прямой линии вокруг оси, перпендикулярной плоскости проекций
При вращении отрезка прямой линии на требуемый угол следует повернуть две его точки на данный угол, а затем соединить эти точки прямой линией.
Если провести ось вращения через одну точку отрезка , тогда сам отрезок превращается в радиус вращения.
В этом случае вращается только одна точка, а другая, лежащая на оси, не меняет своего положения.
Задача: способом вращения вокруг оси, перпендикулярной горизонтальной плоскости проекций, отрезок АВ повернуть на некоторый угол α (рис.94).
Решение
1.Проводится ось вращения АО, перпендикулярно горизонтальной плоскости проекций и проходящей через точку А (А2О2 _|_ П1).
2.Осуществляется вращение отрезка АВ на заданный угол α, радиусом О1В1, по указанной стрелке, до положения О1В11.
3.Определяется горизонтальная проекция отрезка А1В11, который переместился на заданный угол α.
В2 |
|
В12 |
4. Определяется фронтальная проекция точ- |
|
|||
|
|
|
50 |
|
|
|
|

А2
ХО2
О1 ≡ А1
ки В после вращения отрезка АВ (точка В12). Точка А2 соединяется с точкой В12 прямой линией и получается фронтальная проекция отрезка АВ после его вращения А2В12.
В1 Примечание: при вращении отрезка вокруг оси, перпендикулярной к плоскости проекций,
αВ11 величина его не изменяется, а изменяется только
его положение относительно оси проекций.
Рис.94. Вращение отрезка на заданный угол α
Из этого вытекает способ вращения без указания осей вращения, т.е. способ плоскопараллельного перемещения. В этом случае оси вращения не указываются, а объект располагается в существующей системе плоскостей проекций, путем его перемещения, так как это необходимо для частного решения задачи.
Иногда для решения задачи необходимо выполнить вращение вокруг двух осей (или осуществить два перемещения заданного объекта), т.к. одним вращением (или перемещением) задача не может быть решена.
Задача: способом вращения вокруг оси, перпендикулярной горизонтальной плоскости проекций, определить натуральную величину отрезка АВ, заданного своими проекциями (рис.95).
|
А2 |
|
|
|
|
Решение |
|
|
|
О2 ≡ В2 |
1. Через точку В проводим ось вращения ОВ, |
||
|
|
|
|
А12 |
перпендикулярно фронтальной плоскости |
|
|
|
|
|
|
|
проекций (В1О1 _|_ X). Отрезок А2В2 превра- |
Х |
О1 |
|
|
тился в радиус вращения. Точка В2 как лежа- |
||
|
|
|
|
|
|
щая на оси не изменит своего положения. |
|
|
|
В1 |
2. Вращаем фронтальную проекцию отрезка |
||
|
|
|
|
|
|
А2В2 по окружности (как указано стрелкой) до |
|
|
|
|
|
|
положения, когда он расположится парал- |
|
А1 |
|
А11 |
лельно оси проекций Х, т.е. он превратится в |
||
Рис.95. Определение натуральной |
горизонтальную прямую (А12В2 || Х). |
|||||
величины отрезка АВ способом вращения
4. Горизонтальная проекция точки А1 перемещается по прямой, параллельной оси проекций до положения А11. Горизонтальная проекция отрезка после вращения А11В1 будет являться натуральной величиной отрезка АВ.
Задача: способом вращения вокруг осей, перпендикулярных плоскостям проекций, определить угол наклона треугольника АВС, заданного своими ко-
51

ординатами к горизонтальной плоскости проекций, и его натуральную величи-
ну. А(60,10,20), В(75,27,35), С(95,7,10) (рис.96).
В2 |
О12 В12≡О22 |
А12 |
С22 |
F2 |
α |
|
|
С2 |
А2 ≡ О12 |
|
|
С12 |
|
О |
|
Х |
|
||
А1≡О11 |
|
|
|
С1 |
А11 |
|
|
F1 |
|
|
|
|
|
|
|
В1 |
Н.В. |
|
|
|
В11≡О21 |
|
|
С11 |
F11 |
|
C21 |
|
|
||
Рис.96. Определение угла наклона плоскости треугольника АВС и его натуралньой величины, способом вращения вокруг осей перпендикулярных к плоскостям проекций
Решение 1. Первым вращением вокруг оси О1, перпендикулярной горизонтальной
плоскости проекций, проходящей через точку А, треугольник АВС преобразуем во фронтально-проецирующую плоскость.
При вращении треугольник должен расположиться перпендикулярно фронтальной плоскости проекций П2 и спроецироваться на этой плоскости в прямую линию.
Для этого необходимо:
а) в плоскости треугольника АВС из точки А провести горизонталь треугольника АF (А2F2 || Х – фронтальная проекция горизонтали, А1F1 – горизонтальная проекция горизонтали).
б) через точку А провести ось вращения О1, перпендикулярно горизонтальной плоскости проекций.
в) вращением горизонтальной проекции треугольника А1В1С1 расположить его так, чтобы горизонтальная проекция горизонтали А1F1 оказалась перпендикулярной оси проекций Х. Тогда горизонтальная проекция треугольника А1В11С11 расположится перпендикулярно фронтальной плоскости проекций. В этом слу-
чае фронтальная проекция треугольника спроецируется в прямую линию
А2В12С12.
Угол наклона плоскости треугольника АВС к горизонтальной плоскости проекций α определяется как угол между прямой А2В12С12 и осью проекций.
52
2. Вращением вокруг второй оси О2, перпендикулярной фронтальной плоскости проекций, проходящей через точку В1, треугольник АВС преобразуется в горизонтальную плоскость:
а) через точку В11 проводим ось вращения О2 перпендикулярно фронтальной плоскости проекций,
б) радиусом равным В12А2С12 поворачиваем треугольник вокруг оси вращения до параллельного положения относительно оси проекций Х (В12А12С22 || Х), в) строим горизонтальную проекцию треугольника В11А11С21, который будет
являться натуральной величиной треугольника АВС (В11А11С21= АВС).
Способ плоскопараллельного перемещения
Исходя из того, что при вращении оригинала или его элемента вокруг осей, перпендикулярных плоскостям проекций, величина его не изменяется, а изменяется только положение относительно существующей системы плоскостей проекций, вытекает способ вращения без указания осей, т.е. способ плоскопараллельного перемещения.
Суть способа состоит в том, что объект перемещается в пространстве так, как это необходимо для перехода от общего решения задачи к частному.
Фактически действие - перемещение объекта происходит так же, как и при вращении вокруг осей, перпендикулярных плоскостям проекций, но только оси вращения не указываются.
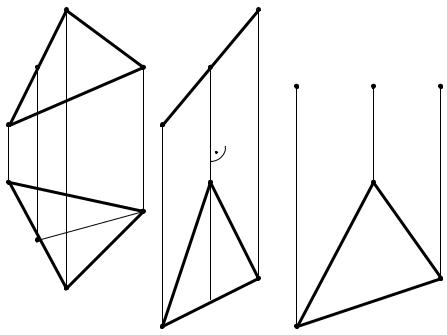
Задача: способом плоскопараллельного перемещения определить натуральную величину треугольника АВС (рис.97).
Решение задачи сводится к тому, что необходимо выполнить два перемещения треугольника АВС в существующей системе плоскостей проекций.
Первым перемещением треугольник преобразуется в проецирующую плоскость, а вторым – в плоскость уровня.
В нашем случае первым перемещением треугольник преобразуется во фронтально-прецирующую плоскость, а вторым – в горизонтальную плоскость.
53
|
|
|
С2 |
|
|
С12 |
|
|
|
|
|
|
||
|
|
F2 |
|
|
В2 F12≡ В12 |
|
А22 |
В22 |
С22 |
|||||
А2 |
|
|
|
|
А12 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В11 |
|
|
|
В21 |
|
|
|||
А1 |
|
|
|
|
|
|
||||||||
В1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
|
F1 |
|
|
|
|
|
|
Н.В. |
|
|
|||
|
|
|
|
С1 |
|
|
|
|
|
|
|
|
|
С21 |
|
|
|
|
|
|
|
С1 |
|
|
|
|
|
||
|
|
|
|
|
А1 |
F11 |
|
А21 |
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
||||
Рис.97. Определение натуральной величины треугольника АВС способом плоскопараллельного перемещения
Для этого:
1.В треугольнике проводим горизонталь плоскости BF.
(B2F2 || X – фронтальная проекция горизонтали, а B1F1 – горизонтальная проекция горизонтали).
2.Перемещаем треугольник так, чтобы он расположился горизонтальной про-
екцией горизонтали перпендикулярно оси проекций (B11F11 Х).
В этом случае он окажется фронтально-проецирующим и фронтальная проекция его будет выглядеть в виде отрезка прямой линии А12В12С12.
3. Вторым перемещением треугольник преобразуется в горизонтальную плоскость. Располагаем его фронтальную проекцию – прямую линию А22В22С22, равную А12В12С12 так, чтобы она оказалась параллельно оси проекций.
Горизонтальная его проекция А21В21С21 будет равна натуральной величине треугольника АВС (А21В21С21 =АВС).
Примечание: другие способы преобразования чертежа в данном пособии не излагаются. Необходимо обратиться к учебникам по начертательной геометрии.
54

Поверхности
Поверхность – совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону.
Линию, которая образует поверхность в каждом ее положении, называют образующей, а линия, по которой перемещается образующая, называется направляющей.
Классификация поверхностей
Линейчатые и нелинейчатые поверхности
Поверхность, которая может быть образована прямой линией, называется линейчатой (коническая, цилиндрическая, торс, цилиндроид, коноид и др.).
Поверхность, для которой образующей может быть только кривая, называется нелинейчатой или кривой (сфера, тор, эллипсоид, парабалоид и др.).
Развертываемые и неразвертываемые поверхности
Если поверхность можно развернуть так, что она совместится всеми своими точками с плоскостью без складок и разрывов, то такая поверхность называется развертываемой.
К таким поверхностям относятся только линейчатые с одной направляющей (коническая, цилиндрическая, торс).
Все кривые поверхности и линейчатые с двумя направляющими являются неразвертываемыми (сфера, тор, эллипсоид и др.).
Линейчатые поверхности с одной направляющей
1. Цилиндрическая поверхность
Эта поверхность образуется прямой линией, которая при перемещении сохраняет параллельность некоторой заданной прямой линией и проходит через все точки некоторой кривой линии – направляющей (рис.98).
S
L |
S – направление образующей |
A |
LA || S – образующая |
|
T |
|
ТА – направляющая |
Рис.98. Образование цилиндрической поверхности
Цилиндрические поверхности различаются по виду нормального сечения (сечение, перпендикулярное образующим).
55
Если в сечении образуется кривая второго порядка, то и поверхность будет называться цилиндром второго порядка. В этом случае в сечении могут быть окружность, эллипс, гипербола, парабола и т.п.
Если в сечении получается неопределенная кривая, то такая поверхность называется цилиндром общего вида.
Линия пересечения поверхности с плоскостью проекций называется следом поверхности.
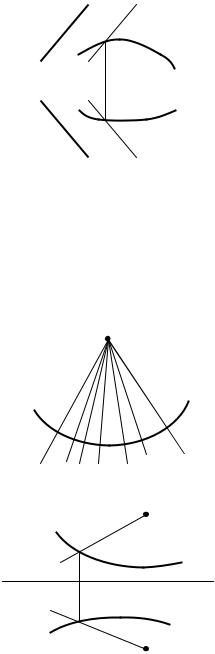
На чертеже цилиндрическая поверхность задается направлением образующей, направляющей (или следом) (рис.99).
|
S2 |
L2 |
S – направление образующей |
|
|
|
|
|
|
|
A2 |
T2 |
S1, S2 – проекции направления образующей |
|
X |
|
|
|
ТА – направляющая |
|
|
|
T1A1, T2A2 – проекции направляющей |
|
|
|
|
||
|
|
|
|
|
|
A1 |
T1 |
LA || S – образующая |
|
|
S1 |
L1 |
L1A1 || S1, L2A2 || S2 – проекции образующей |
|
|
|
|||
Рис.99. Чертеж цилиндрической |
|
|||
|
поверхности общего вида |
|
||
|
|
2. |
Коническая поверхность |
|
Такая поверхность образуется прямой линией, которая проходит через некоторую неподвижную точку – вершину поверхности и последовательно через все точки кривой линии – направляющей (рис.100).
S
T
A
Рис.100. Образование конической поверхности
S2 A2 T2
X
T1
A1
S1
Рис.101. Чертеж конической поверхности общего вида
S – вершина
ТА – направляющая
SA – образующая
На чертеже коническая поверхность задается проекциями вершины и проекциями направляющей (или следом) (рис.101).
Если направляющими будут кривые линии второго порядка, то такие поверхности будут называться конусами второго порядка.
56
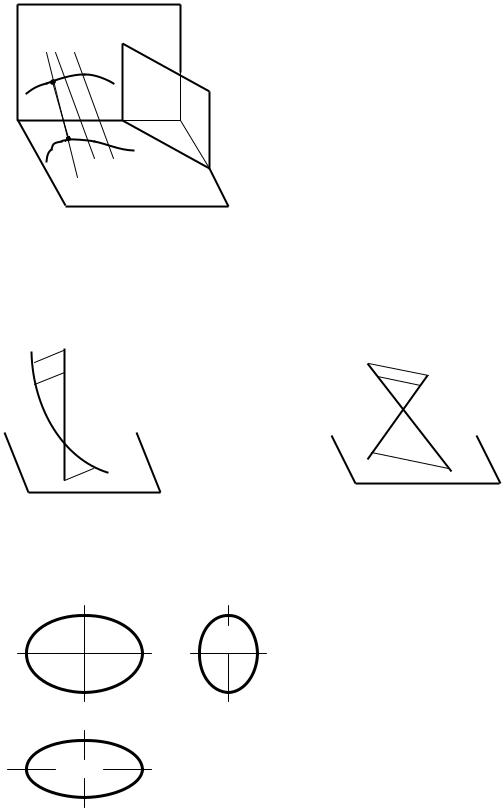
Линейчатые поверхности с двумя направляющими
|
|
|
Цилиндроид |
|
|
П2 |
Поверхность образуется перемещением прямой |
|
|
|
линии, во всех своих положениях сохраняющей |
А |
Т |
параллельность некоторой плоскости, – плос- |
|
|
|
Р |
кости параллелизма и пересекающей две кри- |
Х |
|
вые линии – направляющие (рис.102). |
|
|
|
|
Р – плоскость параллелизма |
|
А1 |
Т1 |
АА1 || Р – образующая |
|
|
|
ТА, Т1А1 – направляющие |
П1
Рис. 102. Цилиндроид
Коноид
Коноид - это цилиндроид, у которого одна направляющая прямая линия.
|
А |
С |
П2 |
|
AB, CD - |
|
|
Е |
F |
|
|
напрввляющие. |
|
|
X |
|
|
|
П1 - плоскость |
|
|
|
|
|
параллелизма |
||
|
|
|
|
|
|
AC, EF, DB - |
|
|
|
|
|
|
|
|
|
D |
B |
П1 |
образующие, |
|
|
|
параллельные П1 |
||||
Рис.103. Коноид
Косая плоскость
Поверхность образуется как цилиндроид, только две направляющие являются скрещивающимися прямыми линиями.
|
|
|
AB, CD - |
|
A |
C П2 |
напрввляющие |
|
E |
F |
(скрещивающиеся |
|
|
|
прямые) |
|
|
|
П1 - плоскость |
X |
|
||
|
параллелизма |
||
|
D |
B П1 AC, EF, DB - |
|
|
|
|
образующие, |
|
Рис. 104. Косая |
параллельные П1 |
|
|
плоскость |
|
|
Нелинейчатые поверхности второго порядка
Эллипсоид
|
|
Е2 |
Z |
Е3 |
Эллипсоид образуется перемещением |
|||
|
|
|
|
|||||
|
|
|
|
|
A3≡B3 |
|||
|
|
|
|
|
деформирующегося эллипса ABCD, |
|||
А2 |
C2 ≡D2 |
В2 |
D3 |
C3 |
||||
плоскость которого остается параллельно |
||||||||
Х |
F2 |
|
|
F3 |
горизонтальной плоскости проекций П1, |
|||
|
|
и концы которого скользят по эллипсам |
||||||
|
|
|
|
|
|
|
||
|
|
D1 |
|
О |
Y |
|||
|
|
|
АFBE, DFCE (рис.105). |
|||||
A1 |
E1 ≡F1 |
B1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
C1 Y
Рис. 105. Чертеж элипсоида
57
|
|
|
|
|
|
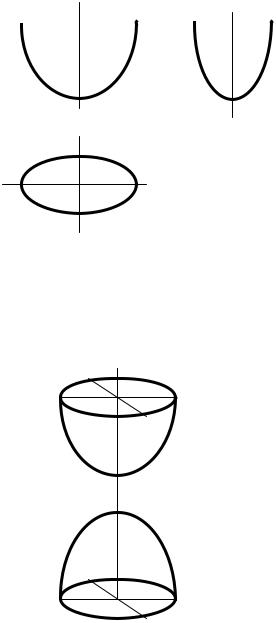
Эллиптический параболоид |
|||
А2 |
|
D2≡C2 |
Z |
A3≡B3 |
|
||||
|
|
B2 |
D3 |
|
|
C3 |
Эллиптический параболоид образуется |
||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перемещением деформирующегося эл- |
|
|
|
|
|
|
|
|
|
липса ABCD, плоскость которого оста- |
|
|
|
F2 |
|
|
F3 |
ется параллельно горизонтальной |
||
X |
|
|
|
|
|
|
|
Y |
плоскости проекций П1, и концы кото- |
|
|
|
|
|
|
||||
|
|
|
D1 |
|
O |
|
|
|
рого скользят по параболам AFB, CFD |
A1 |
F1 |
B1 |
|
|
|
|
(рис.106). |
||
|
|
|
|
|
|
|
|
|
|
C1 Y
Рис. 106. Чертеж элиптического параболоида
|
|
|
Двуполостный гиперболоид |
||
|
С |
|
|
|
|
А |
О |
В |
Он состоит из двух полостей, простираю- |
||
|
|
||||
|
D |
|
щихся в бесконечность. |
||
|
|
|
Каждая из полостей получается в резуль- |
||
|
|
|
тате движения деформирующихся эллипсов |
||
|
|
|
ACBD и A1C1B1D1, плоскости которых оста- |
||
|
C1 |
|
ются перпендикулярными к оси поверхности |
||
|
|
ОО |
1 |
||
A1 |
О1 |
B1 |
и концы осей которого скользят по ги- |
||
перболам (рис.107). |
|||||
|
D1 |
|
|||
|
|
|
|
||
Рис.107. Двуполостный гиперболоид
58
Циклические поверхности
Эти поверхности образуются окружностью переменного радиуса, центр которой перемещается по некоторой кривой линии – направляющей. Если плоскость окружности остается перпендикулярный к заданной направляющей кривой, по которой движется окружность, то образуется циклическая поверхность, называемая каналовой (рис. 108).
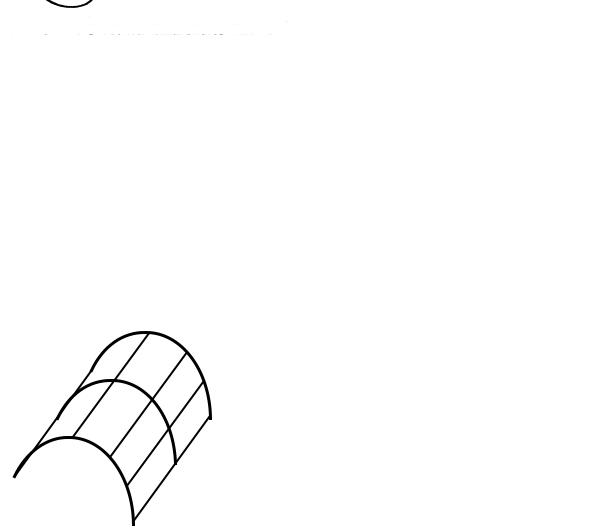
Если диаметр окружности, перемещающейся по кривой линии, постоянный, то циклическая поверхность называется трубчатой (рис. 109).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 108. Каналовая поверхность |
|
|
|
Рис. 109. Трубчатая поверхность |
Поверхности, задаваемые каркасом
Такие поверхности задаются некоторым числом линий, принадлежащих данной поверхности (рис. 109).
Примером каркасных поверхностей служат поверхности корпусов самолетов, судов, вагонов, автомобилей.
K
|
M |
ABC, DEF, KMN – одна группа линий, |
|
D |
E |
||
параллельна друг другу. |
|||
|
N |
||
|
|
ADK, BEM, CFM – другая группа линий, |
|
В |
|
тоже параллельные между собой. |
|
А |
F |
|
|
|
С |
|
|
|
Рис. 110. |
|
Поверхности графические
Эти поверхности задаются графически, т.е. черчением или рисованием.
К таким поверхностям относятся поверхности земной коры. Земная поверхность задается совокупностью ее горизонталей (топографические карты).
59
