umm_2001

2. Если кривая АВ задана в явном виде уравнением y = φ(x), x [a;b], где

φ(x) – непрерывно дифференцируемая функция, тогда

С помощью криволинейного интеграла I рода можно вычислить длину l

кривой АВ плоской или пространственной линии по формуле l = ∫ dl .

AB

Пример 1

Вычислите криволинейный интеграл ∫xy2dl , где L – отрезок прямой

L

между точками О(0;0) и A(4;3).

51

6. Криволинейный интеграл II рода

Пусть на плоскости Oxy задана непрерывная кривая АВ и в каждой точке дуги определена вектор-функция fr = P(x, y)ri +Q(x, y)rj , т. е. в каждой точке этой дуги определены функции P(x; y) и Q(x; y) . Разобьем эту дугу на n эле-

ментарных дуг точками A = M0 , M1, M2 ,..., Mn = B . Выберем на каждой из дуг произвольную точку M i (αi ;βi ) и найдем значения функций в этой точке

P(αi ;βi ) и Q(αi ;βi ) .

условии, что длины всех элементарных дуг стремятся к нулю и этот предел не зависит ни от способа разбиения дуги АВ на элементарные дуги, ни от способа выбора точек Mi на каждой из них, то он называется криволинейным интегралом

52

от функцииurf = P(x, y)ri +Q(x, y)rj по координатам x и y дуги АВ в направлении

Ф = P(x; y; z)i +Q(x; y; z) j + R(x; y; z)k , определенная в каждой точке данной

кривой. Разобьем дугу АВ на n элементарных дуг, на каждой из которых выберем произвольную точкуМi (αi ;βi ; γi ) (см. рис. 14).

Рис. 14. Разбиение кривой интегрирования АВ на элементарные дуги

Составим интегральную сумму:

n

∑[P(αi ;βi ; γi ) xi +Q(αi ;βi ;γi ) yi + R(α ;βi ;γi ) zi ].

i=1

Если существует предел этой интегральной суммы при условии, что длины всех элементарных дуг стремятся к нулю и этот предел не зависит ни от способа разбиения дуги АВ на элементарные дуги, ни от способа выбора точек

Mi на каждой из них, то он называется криволинейным интегралом от функ-

направлении от точки А к точке В или криволинейным интегралом II рода

и обозначается

53

Если кривая АВ гладкая, а функции Р(x,y,z), Q(x,y,z) и R(x,y,z) непрерывные на кривой АВ, то криволинейный интеграл II рода существует. Отметим некоторые свойства криволинейного интеграла II рода:

1. При изменении направления интегрирования интеграл изменяет свой

знак на противоположный ∫ Pdx +Qdy = −∫ Pdx +Qdy .

АВ ВА

2. Если кривая АВ разбита точкой С на две части АС и СВ, то интеграл по всей кривой равен сумме интегралов по ее частям

∫ Pdx +Qdy = ∫ Pdx +Qdy + ∫ Pdx +Qdy .

3. Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки, а зависит только от направления.

Рассмотрим два случая вычисления криволинейного интеграла II рода. Если кривая АВ задана параметрическими уравнениями x = x(t), y = y(t) ,

где α ≤t ≤β, то криволинейный интеграл II рода определяется по формуле

менной силы F(P(x, y);Q(x, y)) или Ф(P(x; y; z),Q(x; y; z), R(x; y; z)) на криволи-

нейном участке АВ соответственно по формулам

54

Пример 1

Вычислите криволинейный интеграл II рода ∫(x − y)2 dx + (x + y)2 dy , где

L

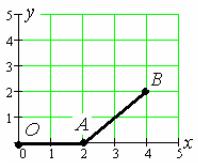
L – ломаная ОАВ, имеющая следующие координаты точек О(0,0), А(2,0), В(4,2).

Решение

Ломаную ОАВ можно представить как сумму двух отрезков ОА и АВ, следовательно, криволинейный интеграл II рода вдоль нее есть сумма криволи-

Рис.15. Кривая интегрирования ОАВ

Составим уравнения отрезков ОА и АВ соответственно: y = 0, 0 ≤ x ≤ 2 и

в пространстве от точки А(1;0;2) до точки В(3;1;4).

55

Решение

Составим канонические уравнения прямой, проходящей через точки А и В: 3x −−11 = 1y−−00 = 4z −−22 x 2−1 = 1y = z −2 2 =t , которые позволяют перейти к параметрической форме x = 2t +1, y =t, z = 2t + 2 .

Определим дифференциалы функций x = x(t), y = y(t) , z = z(t) : dx = 2dt, dy = dt, dz = 2dt .

Установим интервал изменения параметра t :

x=1 1 = 2t +1 t1 = 0 ,

x=3 3 = 2t +1 t2 =1.

Найдем работу переменной силы вдоль отрезка прямой

Задания для контрольной работы № 9

441 – 455. С помощью двойного интеграла вычислите площадь фигуры, ограниченной данными линиями. Сделайте чертеж.

56

первой координатной четверти.

58

первой координатной четверти.

481 – 490. Вычислите криволинейный интеграл II рода.

481. ∫x2 ydx + xy2dy , где L – кривая, заданная параметрическими уравне-

ки (1;е).

59

489. ∫(x3 − y2 )dx + xydy , где L – дуга кривой y = 2x от точки (0;1) до точ-

L

ки (1; 2).

490. ∫xydx +( y − x)dy , где L – дуга кривой y2 = x от точки (0;0) до точки

L

(1;1).

Вопросы к экзамену

1.Понятие функции двух переменных, ее область определения, график функции, линии уровня.

2.Определение частных производных первого порядка функции двух переменных.

3.Уравнения касательной плоскости и нормали к поверхности.

4.Понятие производной по направлению и градиента, формулы для их вычисления.

5.Экстремум функции двух переменных, необходимые и достаточные условия экстремума.

6.Понятие ряда, числовые и степенные ряды. Сходимость ряда, необходимый признак сходимости.

7.Знакоположительные ряды. Достаточные признаки сходимости.

8.Знакочередующиеся ряды. Признак Лейбница.

9.Степенные ряды. Область сходимости степенного ряда. Определение и методы ее нахождения.

10.Ряд Маклорена. Разложение основных элементарных функций в ряд Маклорена. Применение рядов при решении дифференциальных уравнений и вычислении определенных интегралов.

11.Понятие двойного интеграла и методы его вычисления.

12.Геометрические приложения двойного интеграла.

13.Понятие криволинейного интеграла I рода и методы его вычисления.

14.Понятие криволинейного интеграла II рода и методы его вычисления.

15.Приложения криволинейного интеграла I рода.

60