
umm_2001
.pdf
Таким образом, областью определения данной функции будет множество точек, координаты которых удовлетворяют системе неравенств (*) и (**). На рис. 1 область определения закрашена более темным цветом.
Пример 2
Найдите область определения функции двух переменных z(x, y) = arcsin x + arccos y .
Решение
Областью определения функции z(x; y) = arcsin x + arccos y является мно-
жество точек плоскости Оху, значения координат которых удовлетворяют системе неравенств:
−1 |
≤ x ≤1 |
(*), |
|
≤ y ≤1 |
(**). |
−1 |
Решения неравенства (*) изображаются на чертеже точками, лежащими на прямых x = −1 и x =1 и между ними, а решением неравенства (**) – точками плоскости Оху, лежащими на прямых y = −1 и y =1 и между ними (рис. 2).
Геометрически область определения функции будет изображаться точками, принадлежащими одновременно горизонтальной и вертикальной полосе. Это будет квадрат. Область определения замкнутая, так как включает в себя точки границы. На рис. 2 она закрашена более темным цветом.
Рис. 2 21

2. Линии уровня функции
Линии на плоскости Оху вида f(x; y) = С называются линиями уровня функции двух переменных z = f (x; y) .
Построение линий уровня, соответствующих различным значениям постоянной величины С, позволяет увидеть характер поверхности, заданной исследуемой функцией.
Сгущение линий уровня означает более быстрое изменение значений функции. Редкое расположение линий уровня характеризует пологую поверхность (значения функции изменяются медленно).
Линии равных высот на физической карте – это пример линий уровня.
Пример 1
Найдите линии уровня функции z = f (x; y) = ex+y .
Решение
Линии уровня функции z(x; y) = ex+y – это семейство кривых на плоско-
сти Оху, описываемое уравнением C = ex+y . Представим это уравнение в другой форме, выполнив следующие преобразования:
C = ex+y ln C = ln ex+y ln C = x + y.
Пусть ln C =C* , тогда y =C* − x (семейство прямых линий) (рис. 3.).
Рис. 3
22

Пример 2
Найдите линии уровня функции z(x; y) = y − x2 .
Решение
Определить линии уровня |
функции z(x, y) = y − x2 как семейства кри- |
вых y = g(x,C) на плоскости Оху |
можно, осуществляя следующие преобразо- |
вания: C = y − x2 y − x2 = C2. |
Пусть C2 =C* , тогда y = x2 +C* , C* ≥ 0 , (се- |
мейство парабол) (рис. 4). |
|
Рис. 4
3. Дифференцирование функции
Разность f ( x0 + x; y0 ) − f ( x0 ; y0 ) = x z
щением по переменной х функции z = f (x; y) в точке P0 (x0 ; y0 ) . Аналогично определяется частное приращение по переменной y :
y z = f (x0 ; y0 + y) − f (x0 ; y0 ) .
Предел отношения частного приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю, называет-
ся частной производной функции z = f (x; y) по этому аргументу:
∂z |
= lim |
x z |
∂z |
= lim |
y z |
|
|
∂x |
x , |
∂y |
y . |
||||
x→0 |
y→0 |
||||||
|
|
23 |
|
|
|
|
|

Используются также обозначения: z′x , z′y , f x′, |
f y′. |
Приращение функции z = f (x + x, y + |
y) − f (x, y) называют полным |
приращением функции z = f (x; y) .
|
Главная, линейная относительно ∆х и ∆у, часть полного приращения |
||||
функции называется полным дифференциалом |
этой функции и обозначается |
||||
dz. |
|
|
|
|
|
|
dz = A x + B y . Можно доказать, что dz = |
∂z dx + ∂z dy . |
|
||
|
|
∂x |
∂y |
|
|
|
Геометрический смысл частных производных z′x |
и z′y |
заключается в том, |
||
что они равны угловым коэффициентам двух касательных |
l1 и l2 |
к линиям пе- |
|||
ресечения поверхности, определяемой уравнением |
z = f (x, y) , |
плоскостями |
|||
y = y0 |
, x = x0 , проходящими через точку М0 (x ; y ) (касательная l1 |
параллельна |
|||
|
0 |
0 |
|
|
|
плоскости Oxz, касательная l2 параллельна плоскости Oуz) (рис. 5).
Значения частных производных z′x и z′y в точке М0 (x0 ; y0 ) соответственно равны z′x =tgα и z′y =tgβ.
Частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной при фиксированном значении у, поэтому ее находят по правилам вычисления производных функций одной переменной (аналогично рассматривается и частная производная по переменной у).
Рис. 5. Геометрический смысл производных z′x и z′y
24

Примеры
Найти частные производные функций двух переменных z = f (x; y) :
|
|
|
|
1) z(x, y) = ln ( x + |
|
|
y ); |
|
|
|
|
y |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2) |
z(x,y) = arctg |
|
|
|
|
|
+ |
1 . |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1. |
Вычисление |
частных |
|
|
производных |
z′x |
|
|
|
и |
|
|
z′y |
функции |
|||||||||||||||
z(x, y) = ln ( x + y ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z′x = |
∂ |
|
(ln ( x + y ))= |
1 |
|
|
|
∂ |
( |
x + |
y )= |
|
|
1 |
|
|
|
|
|
1 |
|
= |
|
|
1 |
. |
||||
∂x |
|
x + y |
∂x |
|
x + y |
|
|
2 x |
2x + 2 xy |
|||||||||||||||||||||
z′y = |
∂ |
|
(ln ( x + y ))= |
1 |
|
|
|
∂ |
|
( |
x + |
y )= |
|
1 |
|
|
|
|
|
1 |
|
= |
|
|
1 |
|
. |
|||
∂y |
|
x + y |
|
∂y |
|
x + y |
|
2 y |
|
2 xy + 2 y |
||||||||||||||||||||
|
2. |
Вычисление |
частных |
|
|
производных |
z′x |
|
|
|
и |
|
|
z′y |
функции |
|||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z(x, y) = arctg |
|
+1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z′x = |
∂ |
y |
|
|
|
1 |
|
|
|
∂ |
y |
|
|
|
|
||||||||
|
arctg |
|
+1 |
= |
|
|
|
|
|
|
|
|
|
|
|
+ |
1 |
= |
|||||
|
|
|
y |
|
2 |
|
|
||||||||||||||||
|
|
∂x |
x |
|
|
|
|
|
∂x x |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
+ |
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||
= − |
|
|
|
|
x2 y |
|
|
|
= − |
|
|
|
|
y |
|
|
. |
|
|
||||
(x2 + 2 yx + x2 + y2 )x2 |
2x2 + 2 yx + y2 |
|
|
||||||||||||||||||||
z′y = |
∂ |
y |
|
|
1 |
|
|
|
∂ y |
|
|
|||||||
|
arctg |
|
+1 |
= |
|
|
|
|
|
|
|
|
|
|
+1 |
= |
||
|
|
|
y |
|
2 |
|
|
|||||||||||
|
∂y |
x |
|
|
|
|
|
∂y x |
|
|
||||||||
|
|
|
|
|
|
|
1 + |
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
|
x |
|
= |
|
. |
2x2 + 2 yx + y2 |
||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
y |
− |
|
|
|
= |
|
(y + x) |
2 |
x |
2 |
||||
1 + |
|
|
|
|
|
|
||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
1 |
1 |
= |
|
2x2 + 2 yx + y2 |
x |
||||
|
|
|
4. Производная по направлению и градиент
Пусть функция z = f (x; y) определена в окрестности точки М0(х0; у0). Рас-
смотрим некоторое направление, определяемое единичным вектором er, с коорди-
25
натами cos α, cosβ, где α, β – углы этого вектора с осями Ох, Оy. Проведем через точку М0 ось l , направление которой совпадает с направлением вектора e , возьмем на этой оси произвольную точку M (x; y) и обозначим через l величину на-
|
|
uuuur |
|
|
|
правленного отрезка M0M указанной оси. Из аналитической геометрии известно, |
|||||
что |
координаты |
точки |
M (x; y) |
определяются |
равенствами |
x = x0 +l cos α, y = y0 +l cosβ. |
Если функция |
z = f (x; y) имеет в точке l = 0 |
|||
производную по переменной l , то эта производная называется производной по направлению l от функции z = f (x; y) в точке М0(х0;у0) и обозначается симво-
лом ∂∂zl . Эта производная может быть вычислена по формуле
∂∂zl = ∂∂xz cos α + ∂∂yz cosβ.
Производная zl′(x; y) характеризует скорость изменения функции в на-
правлении l.
Пример
Вычислить производную функции z(x; y) =5x4 −3x − y −1 в точке
uuur
М(2; 1) по направлению вектора MN , где N(5; 5).
Решение
Нахождение производной zl′(x; y) по направлению MN согласно формуле zl′(x; y) = z′x cos α + z′y cosβ связано с определением частных производных z′x ,
z′y и направляющих косинусов cosα, cosβ. |
|
||||||
Вычислим частные производные |
z′x и z′y |
в точке М(2; 1): |
|||||
z′x |
= |
|
∂ |
|
(5x4 −3x − y −1)= 20x3 −3, |
z′x (2;1) = 20 23 −3 =157, |
|
|
∂x |
||||||
z′y |
= |
∂ |
(5x4 −3x − y −1)= −1, |
z′y (2;1) = −1. |
|||
∂y |
|||||||
26

|
|
|
|
|
|
|
|
|
|
uuuur |
|
|
|
|
Найдем направляющие косинусы cos α и cosβ вектора MN . Для этого вы- |
||||||||||||||
числим |
|
uuuur |
Они равны |
uuur |
={5 − 2; 5 −1} ={3; 4}. |
Мо- |
||||||||
координаты вектора MN . |
MN |
|||||||||||||
|
|
uuuur |
|
|
2 |
2 |
|
|
|
|
x |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
дуль |
вектора равен |
MN |
|
= |
3 + 4 |
|
=5 |
. |
Тогда |
cosα = |
uuuur |
= |
5 |
, |
|
|
|
|
|
|
|
|
|
|
|
MN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosβ = uuuury = 4 .
MN 5
uuur
Вычислим производную zl′(x; y) по направлению MN в точке М(2; 1): zl′(2;1) = z′x (2;1) cosα + z′y (2;1) cosβ =157 53 + (−1) 54 = 4675 = 93,4 .
Градиентом функции z = f (x, y) в точке M0 называется вектор, обозна-
чаемый символом gradz и имеющий координаты, соответственно равные про-
|
∂z |
|
∂z |
, вычисленным в точке M0 |
|
∂z |
|
∂z |
|
изводным |
∂x |
, |
∂y |
. Таким образом, gradz= |
∂x |
, |
|
|
|
|
|||||||||
|
|
|
|
|
∂y . |
||||
Производная по направлению zl′ равна скалярному произведению гради-
ента gradz и единичного вектора, задающего направление l, ∂∂zl = (gradz, l).
Градиент функции gradz в данной точке характеризует направление максимальной скорости возрастания функции в этой точке.
Если в точке M(x; y) модуль градиента функции отличен от нуля, то в точке M(x; y) градиент перпендикулярен линии уровня, проходящей через данную точку.
Пример
Найти градиент gradz функции z(x; y) = x ln(x + y) и его модуль в точке
М(-1; 2).
Решение
Координаты вектора gradz можно найти, если вычислить значения частных производных z′x и z′y в точке М(-1; 2):
27

z′x = |
∂ |
|
(x ln (x + y))= ln(x + y) + |
x |
|
, z′x (−1; 2) = ln1−1 = −1, |
|||
∂x |
x + y |
||||||||
|
|
|
|
|
|
||||
z′y = |
∂ |
|
(x ln(x + y))= |
x |
, z′y (−1; |
2) = −1. |
|||
∂y |
|
x + y |
|||||||
|
|
|
|
|
|
|
|||
Градиент функции gradz = {−1; −1} в точке М(-1; 2) перпендикулярен ли-
нии уровня, которая проходит через данную точку. Направление максимально быстрого возрастания функции z = f (x; y) и направление градиента в точке
М(-1; 2) совпадают.
Модуль градиента функции gradz = {−1; −1} в точке М(-1; 2) – это длина
вектора градиента: gradz = (−1)2 + (−1)2 = |
2 . |
|
|
5. Касательная плоскость и нормаль к поверхности |
|
||
Пусть функция z = f (x; y) дифференцируема в точке (x0 ; y0 ) |
некоторой |
||
области |
D . Рассечем поверхность S, изображающую функцию z, |
плоскостя- |
|
миx = x0 |
и y = y0 (рис. 6). Плоскость x = x0 |
пересекает поверхность S по некото- |
|
рой линии z0 ( y) , уравнение которой получается подстановкой в выражение ис-
ходной функции z = f (x; y) вместо х числа х0. Точка M0 (x0 ; y0 ; f (x0 ; y0 )) при-
надлежит кривой z0 ( y) . В силу дифференцируемости функции z в точке М0
функция z0 ( y) также является дифференцируемой в точке y = y0 . Следователь-
но, в этой точке в плоскости x = x0 к кривой z0 ( y) может быть проведена каса-
тельная l1.
Проводя аналогичные рассуждения для сечения y = y0 , построим каса-
тельную l2 к кривой z0 (x) в точке x = x0 . Прямые l1 и l2 определяют плоскость
(P) , которая называется касательной плоскостью к поверхности S в точке М0
(рис. 6).
28
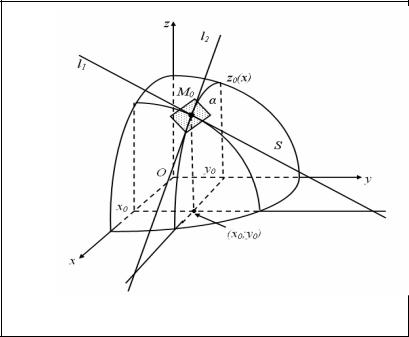
|
|
Рис.6 |
Уравнение |
плоскости |
(P) , которая проходит через точку |
M0 (x0 ; y0 ; f (x0 ; y0 )) |
имеет вид: A(x − x0 )+ B(y − y0 )+C (z − z0 )= 0 . |
|
После преобразований это уравнение можно записать следующим обра-
зом: z − z0 = fx′(x0 ; y0 ) (x − x0 )+ fy′(x0 ; y0 ) (y − y0 ).
Прямая, проходящая через точку М0 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется нормалью к по-
верхности в точке М0.
Уравнения нормали имеет вид:
x − x |
= |
y − y |
= |
z − z |
0 |
. |
0 |
0 |
|
||||
fx′(x0 ; y0 ) |
fy′(x0 ; y0 ) |
−1 |
|
Если функция z = f (x; y) задана неявно уравнением F(x, y, z) = 0 , то уравнения касательной плоскости к данной поверхности и нормали к ней в точке М0 будут иметь вид:
Fx′(x0 , y0 , z0 )(x − x0 ) + Fy′(x0 , y0 , z0 )( y − y0 ) + Fz′(x0 , y0 , z0 )(z − z0 ) = 0 ,
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
Fx′(x0 , y0 , z 0 ) |
Fy′(x0 , y0 , z0 ) |
Fz′(x0 , y0 , z0 ) |
||||
|
|
|
29

Пример
Написать уравнения касательной плоскости и нормали к поверхности z(x; y) =sin xy в точке М(π; 1; 0).
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем частные производные |
z′x |
и z′y |
|
функции |
z(x; y) =sin |
x |
в точке |
||||||||||||||
|
y |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М(π;1;0): z′x = |
∂ |
|
x |
|
|
1 |
|
|
|
x |
, z′x (π;1;0)= −1, |
|
|
|
|||||||
sin |
|
= |
cos |
|
|
|
|
||||||||||||||
|
y |
|
y |
|
y |
|
|
|
|||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
z′y = |
∂ |
|
|
|
x |
|
|
x |
|
|
x |
|
z′y (π;1;0) |
|
|
|
|||
|
|
|
sin |
|
= − |
|
cos |
, |
= π. |
|
|
||||||||||
|
|
|
|
|
2 |
y |
|
|
|||||||||||||
|
|
|
|
|
∂y |
|
y |
|
y |
|
|
|
|
|
|
||||||
Уравнение касательной плоскости в точке М(π ; 1; 0): z −0 = −1(x −π) + π( y −1) x −πy + z = 0.
Канонические уравнения нормали в точке М(π; 1; 0): x−−1π = yπ−1 = −z1
или x −1 π = y−π−1 = 1z .
7. Частные производные второго порядка
Частная производная от частной производной функции z = f (x; y) назы-
вается частной производной второго порядка. Приняты следующие обозначе-
ния для частных производных второго порядка:
∂ ∂z = z′′xx = ∂x ∂x
но два раза;
∂ ∂z = z′′xy = ∂y ∂x
fxx′′(x; y) – функция дифференцируется по х последователь-
fxy′′(x; y) – функция сначала дифференцируется по х, а ре-
зультат затем дифференцируется по у;
30
