
umm_2001
.pdf421-430. Найти градиент функции z = f (x, y) в точке M0 (x0 ; y0 ) и произ-
водную в направлении, идущем от этой точки к точке M1(x1; y1) :
421. |
z = x2 + xy + y2 +3 , |
М0(3;0), М1(1;1). |
||
422. |
z = x2 + xy + y2 +3 |
М0(3;2), М1(2;1). |
||
423. |
z = x3 |
+ y2 − xy + 4 |
М0(2;1), М1(-1;2). |
|
424. |
z = 2x3 + y3 |
− x2 − y |
М0(-1;2), М1(1;1). |
|
425. |
z = x2 |
+3y2 |
− xy2 |
М0(1;1), М1(-1;-2). |
426. |
z = x4 |
+ y3 + x2 y |
М0(2;-1), М1(1;2). |
|
427. |
z = x3 |
+ 4 y3 |
− x2 y2 |
М0(1;1), М1(0;-2). |
428. |
z = 2x2 −3y3 + 4xy |
М0(-3;1), М1(4;2). |
||
429. |
z =5x2 −3xy + 4 y2 |
М0(2;-1), М1(1;-2). |
||
430. |
z =3x4 − 4 y3 + x |
М0(1;1), М1(2;1). |
||
431-440. Найти экстремум функции:
431.z = x3 − 2 y2 −3x +6 y +1.
432.z = x3 − 2x − 4 y3 +12 y −1.
433.z = x2 − 2x − 4 y3 +12 y .
434.z = x3 +3y3 −9x −9 y2 +16 .
435.z = x3 + y2 −6xy −39x +18y + 20.
436.z = 2x3 + 2 y3 −6xy +5 .
437.z = x3 +3xy2 −15x −12 y +1.
438.z = x3 +8y3 −6xy +1.
439.z = 2x3 − 2 y2 −6x + 4 y +1.
440.z = x2 − 2x −4 y3 +12 y +5 .
441-450. Найдите наибольшее и наименьшее значения функции z = f (x; y) в заданной области:
41
441. Функции |
z =3x + y − xy |
в |
области |
D |
|
|
|
, ограниченной линиями |
|||||||||||||
y = x, y = 4, x = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
442. Функции |
z = x2 − 2 y2 + 4xy −6x −1 в области |
|
|
, ограниченной ли- |
|||||||||||||||||
D |
|||||||||||||||||||||
ниями y + x =3, y = 0, x = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
443. Функции z = x2 + 2xy − 4x +8y |
в области |
|
|
|
|
|
|
, ограниченной линиями |
|||||||||||||
D |
|||||||||||||||||||||
y = 2x2 , y =8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
444. Функции |
z =5x2 −3xy + y2 |
в |
области |
|
|
|
|
|
, ограниченной линиями |
||||||||||||
D |
|||||||||||||||||||||
x =1, y = 0, x = 0, y =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
445. Функции z = x2 + 2xy − y2 − 4x в области |
|
|
|
|
, ограниченной линиями |
||||||||||||||||
D |
|||||||||||||||||||||
x − y +1 = 0, x =3, y = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
446. Функции z = x2 + y2 − 2x − 2 y |
в области |
|
|
|
, ограниченной линиями |
||||||||||||||||
D |
|||||||||||||||||||||
x + y =1, x = 0, y = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
447. Функции |
z = 2x3 − xy2 + y2 |
в |
области |
|
|
|
, ограниченной линиями |
||||||||||||||
D |
|||||||||||||||||||||
x =1, y = 0, x = 0, y = 6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
448. Функции |
z =3x +6 y − x2 − xy − y2 в области |
|
, ограниченной ли- |
||||||||||||||||||
D |
|||||||||||||||||||||
ниями x =1, y = 0, x = 0, y = 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
449. Функции |
z = x2 + 2xy −10 |
в области |
|
|
|
, ограниченной линиями |
|||||||||||||||
|
D |
||||||||||||||||||||
y = x2 −4, y = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
450. Функции |
z = xy − 2x − y в области |
|
, ограниченной линиями |
||||||||||||||||||
D |
|||||||||||||||||||||
x =3, y = 0, x = 0, y = 4 .
III.КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
1. Понятие двойного интеграла и его свойства
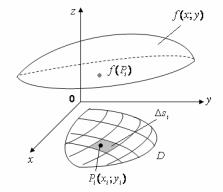
Пусть в области D плоскости Oxy задана непрерывная функция z = f (x; y) . Разобьем область D на n малых частей, площади которых обозна-
42
n
чим через si , причем ∑ si равна площади области D (см. рис. 8). В каждой
i=1
площадке выберем произвольную точку Pi (xi ; yi ) и найдем значение функции z
n
в ней: zi = f (xi ; yi ) . Составим интегральную сумму вида: ∑ f (xi ; yi ) si . Если
i=1
существует предел этой суммы при условии, что каждая из элементарных площадок стягивается в точку и этот предел не зависит ни от способа разбиения области D на элементарные области, ни от способа выбора в них точ-
киPi (xi ; yi ) , то он называется двойным интегралом от функции f (x, y) по об-
ласти D и обозначается ∫∫ f (x, y)ds . Таким образом,
D |
|
|
n |
∫∫ f (x, y)ds =limn→∞ |
∑ f (xi ; yi ) si . |
D |
i=1 |
Геометрический смысл двойного интеграла состоит в том, что величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела, основанием которого служит область D, а сверху тело ограничено поверхностью z = f (x; y) .
Рис. 8. Область интегрирования функции f (x;y)
Свойства двойного интеграла идентичны свойствам определенного интеграла:
1) постоянный множитель подынтегральной функции можно выносить за
знак интеграла ∫∫сf (x; y)ds = c∫∫ f (x; y)ds ;
D D
43
2) интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых функций
∫∫( f (x; y)+ g(x; y))ds = ∫∫ f (x; y)ds + ∫∫g(x; y)ds ;
D D D
3)если подынтегральная функция равна единице, то интеграл равен площади области интегрирования ∫∫ds = SD ;
D
4) если область интегрирования D разбита на две части D1 и D2 , то
∫∫ f (x; y)ds = ∫∫ f (x; y)ds + ∫∫ f (x; y)ds .
D |
D1 |
D2 |
2. Вычисление двойного интеграла в декартовой системе координат
Рассмотрим, как вычисляется двойной интеграл. Вычисление двойного интеграла в декартовой системе координат сводится к вычислению повторного интеграла по области интегрирования. Если область D ограничена линиями x = a; x =b; y = φ1(x); y = φ2 (x) , причем φ1(x) ≤ φ2 (x) , то интеграл будет ра-
вен ∫∫ |
b |
|
φ2 ( x) |
f (x, y)dxdy = ∫dx |
|
∫ |
|
D |
a |
|
φ1 ( x) |
f (x, y)dy . Сначала вычисляется внутренний ин-
теграл, считая x постоянной, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по x в пределах от a до b . Если же об-
ласть интегрирования D |
ограничена |
прямыми y = c и |
y = d , |
кривыми |
|
x = ψ1( y) и |
x = ψ2 ( y) , |
причем |
ψ1( y) ≤ ψ2 ( y) , |
то |
получим |
|
d |
|
ψ2 ( y) |
∫∫ f (x, y)dxdy = ∫dy |
|
∫ |
|
D |
c |
|
ψ1 ( y) |
f (x, y)dx . Еще раз отметим, что при вычислении
внутреннего интеграла здесь считаем переменную y постоянной.
Пример 1
Вычислить ∫∫(x + 2 y)dxdy , где область D ограничена линиями
D
y = x2 , y = 0, x + y − 2 = 0.
44

Решение
На рис. 9 изобразим область интегрирования
Рис. 9 Из рисунка видно, что наш интеграл можно вычислить двумя способами,
взяв постоянные пределы интегрирования либо по х, либо по y.
1 способ. Если постоянный предел интегрирования взят по x , то область интегрирования надо разбить на две части: от 0 до 1 и от 1 до 2. Тогда
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫(x + 2 y)dxdy = ∫1 dx(x∫(x + 2 y)dy + ∫2 dx(2∫−x (x + 2 y)dy = ∫1 dx(xy |
+ |
2 y2 ) |
|
0x2 + |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
D |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
+∫2 dx(xy + |
2 y2 ) |
|
02−x = |
∫1 (x3 + x4 )dx + ∫2 (2x − x2 + (2 |
− x)2 )dx = |
x4 |
|
10 |
+ |
x5 |
|
|
10 +∫2 (4 − 2x)dx = |
||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
1 |
|
2 |
|
|
|
0 |
|
1 |
|
|
|
4 |
|
|
5 |
|
|
|
1 |
|
|
|||||
= |
1 |
+ 1 + 4x |
|
12 −x2 |
|
|
9 |
+ 4(2 −1) |
−(4 −1) = |
9 |
+ |
4 −3 = |
29 . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
12 = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4 |
20 |
20 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 способ. Возьмем внешние пределы интегрирования по y. Тогда интеграл примет вид:
|
|
∫∫ |
|
|
|
|
|
|
|
|
1 |
|
|
|
2−y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(x + 2 y)dxdy = |
∫ |
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
dy |
|
|
(x + 2 y)dx = |
|
|
|
|
|
||||||||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
x2 |
|
|
|
2−y |
1 |
|
(2 |
− y)2 |
|
|
|
|
|
|
2 |
|
|
|
y |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∫dy |
|
|
+ 2 yx |
|
|
y |
= ∫( |
|
|
|
|
|
|
|
|
+ 4 y − 2 y |
|
− |
|
|
− |
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
(2 − y)3 |
|
7 y2 |
|
|
2 y3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ |
− |
− |
4 y2 |
) |
|
|
1 |
= |
− |
1 |
+ |
8 |
+ |
7 |
|
− |
2 |
− |
4 |
= |
29 |
. |
|||||||||||||
|
|
||||||||||||||||||||||||||||||||||
−2 y2 )dy = (− |
6 |
|
|
4 |
|
3 |
|
5 |
|
|
0 |
6 |
6 |
4 |
|
3 |
5 |
20 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
45
Как следует из свойств двойного интеграла, с его помощью можно вы-
числить площадь плоской фигуры по формуле S = ∫∫dxdy .
D
Пример 2
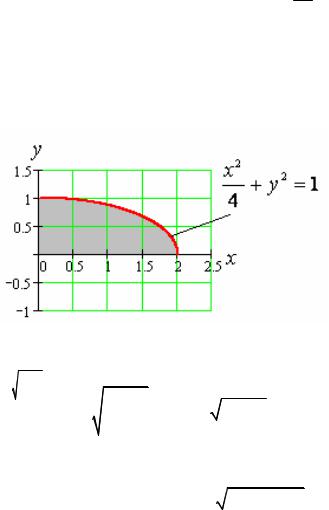
Найти площадь фигуры, ограниченной эллипсом x2 + y2 =1, x ≥ 0, y ≥ 0 . 4
Решение
Область интегрирования, площадь которой мы ищем, изобразим на рис. 10 и определим внешние пределы интегрирования по x .
Рис. 10
|
|
1− |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда S = ∫2 dx |
|
dy = ∫2 |
|
|
|
|
|
|
|
|
∫2 |
|
||||
∫4 |
1− |
x2 |
dx |
= |
1 |
4 − x2 dx = |
||||||||||
|
|
|||||||||||||||
0 |
0 |
|
|
0 |
4 |
|
|
|
|
|
2 |
0 |
|
|||
|
x = 2sin t, |
t = arcsin |
x |
|
|
|
|
|
π |
|
||||||
|
|
|
|
|
|
|
||||||||||
= |
|
|
= 1 |
∫2 |
4 − 4sin2 t 2costdt = |
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
dx = 2costdt, |
0 ≤t ≤ |
π |
|
|
2 |
0 |
|
||||||||
|
2 |
|
|
|
|
|
|
|||||||||
ππ
= 2∫2 cos2 tdt = ∫2 |
(1+ cos 2t)dt = (t + |
1 sin 2t) |
π |
π. |
|
02 = |
|||||
0 |
0 |
|
2 |
|
2 |
3. Вычисление двойного интеграла в полярной системе координат
Часто вычисление двойного интеграла удобнее выполнять в полярной системе координат. Напомним связь полярных и декартовых координат точки.
46
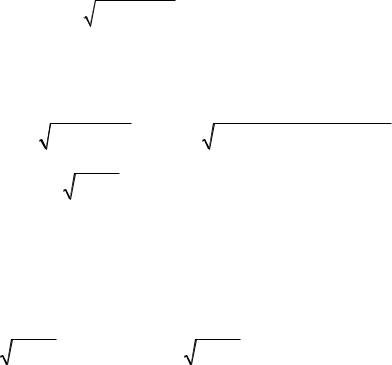
Она задается формулами x =ρcosφ, y =ρsin φ. Пусть область D ограничена лучами φ = α и φ =β и кривыми ρ =ρ1(φ) и ρ =ρ2 (φ) . Тогда двойной интеграл
примет вид : ∫∫ f (x, y)dxdy = ∫∫ f (ρcosφ,ρsin φ)ρdρdφ.
D D
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к повторному интегралу:
|
β |
ρ2 (φ) |
∫∫ρ f (ρcosφ,ρsin φ) dρdφ = ∫dφ ∫ ρ f (ρcosφ,ρsin φ) dρ. |
||
D* |
α |
ρ1 (φ) |
При нахождении внутреннего интеграла аргументφ считается постоян-
ным.
Пример
Вычислить ∫∫ 9 − x2 − y2 dxdy , где область D – круг x2 + y2 ≤9.
Решение
Переход к полярным координатам можно осуществить следующим образом:
∫∫ |
9 − x2 − y2 dxdy = ∫∫ 9 −(ρcosφ)2 −(ρsin φ)2 ρ dρ dφ = |
D |
D |
= ∫∫ρ 9 −ρ2 dρ dφ.
D
Область D в полярной системе координат определяется неравенствами
0 ≤ φ≤ 2π, 0 ≤ρ≤3 (см. рис. 11).
Вычисление двойного интеграла в полярной системе координат:
|
|
|
|
2π |
3 |
|
|
|
|
|
|
1 |
2π |
3 |
|
1 |
∫∫ρ 9 −ρ2 dρ dφ = ∫dφ∫ρ |
9 −ρ2 dρ = − |
∫dφ∫ |
(9 −ρ2 )2 d(9 −ρ2 ) = |
|||||||||||||
D |
|
|
|
0 |
0 |
|
|
|
|
|
|
2 |
0 |
0 |
|
|
|
1 |
2π |
|
3 |
|
|
3 |
|
|
1 |
2π |
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
(9 −ρ2 )2 2 |
|
|
|
|
|
|
|
|
||||||
= − |
|
∫dφ |
|
|
|
|
0 |
= − |
|
∫(0 − 27)dφ =9φ |
0 |
=18π. |
||||
2 |
3 |
|
3 |
|||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47
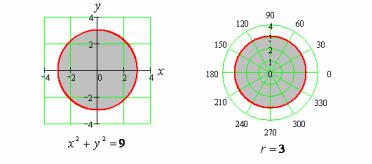
Рис. 11. Область интегрирования D в декартовой и полярной системе координат
4. Приложение двойного интеграла
С помощью двойного интеграла можно вычислить объем цилиндриче-
ского тела по формуле V = ∫∫ f (x; y)dxdy , где z = f (x; y) – уравнение поверхно-
d
сти, ограничивающей тело сверху.
Пример
Найти объем тела, ограниченного поверхностями x2 + y2 − z +1 = 0 и x2 + y2 +3z −7 = 0 .
Решение
Данное тело ограничено двумя параболоидами (рис. 12). Найдем их линию пересечения, решив систему уравнений:
|
2 |
+ y |
2 |
= z −1 |
|
x |
|
|
. |
||
|
2 |
+ y2 = −3z + 7 |
|||
x |
|
||||
|
|
|
|
|
|
Приравняем правые части уравнений и найдем z: z −1 = −3z + 7 z = 2 . Следовательно, линией пересечения параболоидов является окружность x2 + y2 =1, лежащая в плоскости z = 2 . Значит искомый объем V тела равен
разности объемов двух цилиндрических тел V2-V1 с одним основанием (круг единичного радиуса), которые ограничены сверху соответственно поверхностями z = 13 (7 − x2 − y2 ) и z =1+ x2 + y2 .
48

|
|
|
|
|
|
|
|
|
|
Рис. 12 |
|
|
|
|
||
|
|
Вычислим объем тела по формуле |
|
|
|
|
||||||||||
|
|
V =V2 −V1 = ∫∫ |
1 (7 |
− x2 − y2 )dxdy − ∫∫(1+ x2 + y2 )dxdy. |
||||||||||||
|
|
|
|
|
D |
3 |
|
|
|
|
D |
|
|
|
||
|
|
Перейдем |
к |
полярным |
координатам: x2 + y2 =1 ρ =1, 0 ≤ φ≤ 2π, |
|||||||||||
z = |
1 |
(7 −ρ2 ), z =1+ρ2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = 1 |
∫∫(7 −ρ2 )ρdρdφ− ∫∫(1+ρ2 )ρdρdφ = |
|
|
|||||||||||
|
|
|
3 |
D |
|
|
|
|
|
D |
|
|
|
|
||
|
|
|
= 1 2∫π dφ∫1 (7ρ−ρ3 )dρ− 2∫π dφ∫1 (ρ+ρ3 )dρ = |
|
|
|||||||||||
|
|
|
|
3 0 |
0 |
|
|
|
|
0 |
0 |
|
|
|
||
|
|
= |
1 ( |
7 − |
1) φ |
|
02π−(1 |
+ 1) φ |
|
02π= |
13 2π |
− 3 2π |
= |
2 π. |
||
|
|
|
|
|||||||||||||
|
|
|
3 |
2 |
4 |
|
|
|
2 |
4 |
|
|
12 |
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Криволинейный интеграл I рода
Пусть на плоскости Oxy задана дуга АВ и в каждой точке этой дуги определена непрерывная функция f (x; y) . Разобьем эту дугу на n элементарных дуг, li – их длины. Выберем на каждой из них произвольную точку M i (αi ;βi ) и
найдем значение функции в ней f (αi ,βi ) (см. рис. 13).
49

Рис. 13. Разбиение кривой интегрирования АВ на элементарные дуги
n |
|
Составим интегральную сумму вида: ∑ f (αi ;βi ) |
li . Если существует |
i=1 |
|
предел данной интегральной суммы при условии, что все |
li → 0 и он не зави- |
сит ни от способа разбиения дуги АВ на элементарные дуги, ни от способа вы-
бора точек Mi на каждой из них, |
то он называется криволинейным интегра- |
|
лом по длине дуги или интегралом I рода и обозначается ∫ f (x; y)dl : |
||
|
|
AB |
|
|
n |
∫ f (x; y)dl = liml →0 ∑ f (αi ;βi ) li . |
||
AB |
i |
i=1 |
|
||
Вычисление криволинейного интеграла I рода может быть сведено к вы- |
||
числению определенного интеграла. Рассмотрим два случая. |
||
1. Пусть кривая АВ |
задана параметрическими уравнениями |
|
x = x(t), y = y(t), t [α;β], где x = x(t), y = y(t) – непрерывные дифференцируе-
мые функции параметра t , причем точке А соответствует t = α, точке В – зна-
β
чение t =β, α <β. Тогда ∫ |
f (x; y)dl = ∫ f (x(t); y(t)) (xt′ )2 + ( yt′)2 dt . |
AB |
α |
Если кривая АВ задана параметрически в трехмерном пространстве, то криволинейный интеграл от функции f (x; y; z) вычисляется по формуле
50
