umm_201

Данное методическое пособие предназначено для студентов технических специальностей (ЭЛ, Л, В, ПГС, СЖД, БП) с ускоренным временем обучения на заочном отделении. Пособие содержит теоретический материал и практические задания для изучения высшей математики в первом семестре. Кроме того, в нём приведены некоторые математические формулы из курса элементарной математики. При подготовке данного методического пособия авторы опирались главным образом на изданное методическое руководство «Высшая математика» для студентов заочного отделения под редакцией В.И. Белугина, Т.В. Величко, Э.Е. Поповского.

Для успешного изучения курса высшей математики студенту заочного обучения необходимо систематическое посещение установочных занятий, самостоятельное изучение литературы по соответствующим разделам, а также выполнение всех контрольных заданий из данного пособия.

Утверждено редакционно-издательским советом университета.

Авторы:

Т.В. Завьялова, доцент кафедры «Высшая математика», канд. физ.-мат. наук, Т.В. Величко, ст. преподаватель кафедры «Высшая математика»,

Э.Е. Поповский, доцент кафедры «Высшая математика», И.Н. Пирогова, ст. преподаватель кафедры «Высшая математика».

Рецензент:

Г.А. Тимофеева, д-р. физ.-мат. наук, профессор кафедры «Высшая математика».

© Уральский государственный университет путей сообщения (УрГУПС), 2006

ОГЛАВЛЕНИЕ

Введение……………………………………………………………………………...4

Краткие теоретические сведения…………………………………………………...5

1.Матрицы и действия над ними…………………………………………………...5 2. Определители матриц…………………………………………………………….6

3.Решение систем алгебраических уравнений………...…………………………..7

4.Функции и их графики………………...………………………………………….9

Задания для контрольной работы №1……………………………………………..12

5.Предел и производная функции……………...…………………………………15

6.Исследование функций с помощью производной……………………………..20

7.Неопределенный интеграл………………………………………………………24

8.Определенный интеграл…………………………………………………………28

Задания для контрольной работы №2……………………………………………..32 Вопросы для подготовки к экзамену в первом семестре………………………...36

Библиографический список………………………………………………………..38

ВВЕДЕНИЕ

Работа студента над курсом математики на заочном факультете УрГУПС предполагает самостоятельное изучение теоретического материала и выполнение значительного числа задач и упражнений, позволяющих глубже понять содержание курса и выработать необходимые навыки в выполнении стандартных математических операций.

Методическое руководство содержит необходимые теоретические сведения, а также некоторые примеры решения практических задач. Следует отметить, что этих сведений недостаточно не только для последующей сдачи экзамена или зачета, но и для выполнения всех контрольных заданий.

Помимо теоретических сведений в руководстве содержатся варианты заданий для выполнения контрольных работ. Вариант контрольной работы студенту следует выбирать в соответствии с присвоенным шифром.

При выполнении контрольных работ и представлении их на проверку студент должен руководствоваться следующими правилами.

1.Каждая контрольная должна быть выполнена в отдельной тетради и сдана в деканат или отправлена на проверку по почте в деканат заочного факультета.

2.Для получения зачета по контрольной работе студент должен пройти собеседование с преподавателем, где необходимо продемонстрировать понимание хода решения задач в своей контрольной работе.

3.Если при проверке контрольной работы обнаружены ошибки, то студент должен в той же тетради выполнить работу над ошибками и прислать ее в деканат для повторной проверки.

4.Решение задач в контрольной работе должно быть достаточно подробным и логически последовательным. Полезно в тексте решения приводить формулировки теорем и других теоретических сведений, на основании которых делаются заключения.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1. Матрицы и действия над ними

держащиеся в этой таблице, называются элементами матрицы. Матрица является квадратной, если количество строк совпадает с количеством столбцов, то есть n = m .

Две матрицы A и B называются равными, если их размерности равны и равны элементы, стоящие на соответствующих местах.

Матрицы обладают следующими свойствами:

1. Всякую матрицу A можно умножить на число λ . Результатом этого действия будет матрица, каждый элемент которой будет умножен на это число.

ность m ×k ) называется матрица C размерности n ×k , элементы которой равны cij = ai1b1 j + ai2b2 j +K+ aimbmj , где i =1,2,K,n, j =1,2,K,k . Следует отметить, что число столбцов матрицы A должно быть равно числу строк матрицы B .

Матрица, содержащая один столбец, называется вектором-столбцом, а матрица, содержащая одну строку – вектором-строкой.

В экономике с помощью матриц удобно задавать различные наборы показателей. Например, если предприятие выпускает продукцию трёх видов и использует для этого два вида сырья, то нормы расхода сырья для производства продукции можно задать матрицей размерности 3×2 следующим образом: aij – норма расхода i -го сырья для производства j -ой продукции.

2. Определители матриц

Каждой квадратной матрице A порядка n можно поставить в соответствие число, называемое определителем и обозначаемое A . Если матрица раз-

мерности 2 ×2 , то ее определителем является число, которое вычисляется по правилу

Если матрица размерности 3 ×3, то ее определителем является число, вычисляемое по правилу треугольников (правило Саррюса)

a11 a12 a13

A= a21 a22 a23 = a11a22a33 + a12a23a31 + a13a21a32 − a13a22a31 − a11a23a32 − a12a21a33 a31 a32 a33

Вэтой формуле использовано правило треугольников, заключающееся в следующем: сумма произведений по три элемента определителя берется со знаком «+» и со знаком «–» согласно схемам

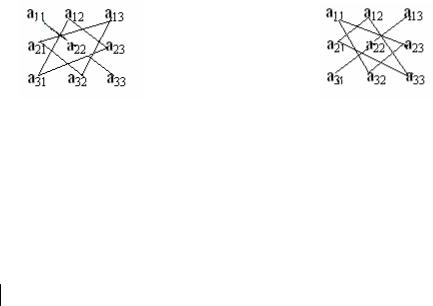
(2.2)

« + » « – »

Здесь элементы a11, a22 , a33 называются элементами главной диагонали, а эле-

менты a13 , a22 , a31 – элементами побочной диагонали.

Другой способ вычисления определителя третьего порядка даётся формулой

3. Решение систем алгебраических уравнений

Рассмотрим систему из трёх уравнений с тремя неизвестными x, y и z :

Решением системы линейных уравнений (3.1) называется такая тройка чисел (x0 , y0 , z0 ) , при подстановке которой в любое уравнение системы (3.1), полу-

чаются верные равенства.

С этой системой связаны следующие четыре определителя:

Правило Крамера. Если ≠ 0 , то система (3.1) имеет единственное решение, которое вычисляется по формулам:

Выписанные здесь определители вычисляются либо по правилу треугольников (2.2), либо по формуле (2.3).

Пример. Найти решение системы уравнений методом Крамера.

− x +3y + 2z = 7

Решение. Согласно методу Крамера нужно вычислить четыре определителя:

Подставив найденные значения x0 , y0 , z0 в любое уравнение исходной системы, можно убедиться, что найденное решение верно.

Ответ. x0 = 7; y0 = 2; z0 = 4 .

4. Функции и их графики

Определение функции. Пусть даны два числовых множества X и Y .

Если каждому элементу x из множества X ( x X ) по некоторому правилу (закону) f поставлено в соответствие вполне определённое значение y из

множества Y ( y Y ), то говорят, что на множестве X определена функция y = f (x) . Тогда X называется областью определения функции y = f (x) . Пере-

менная x называется аргументом функции.

Функция может быть задана либо аналитически, то есть с помощью уравнения, либо с помощью таблицы, содержащей значения x и y . Графиком

функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции. Если функция задана с помощью уравнения, то под областью определения такой функции будем понимать область значений переменной x , допустимых для этого уравнения.

Пример. Найти область определения функции y = x2 + 5x − 6 .

Решение. Поскольку арифметический корень извлекается только из неотрицательных чисел, то областью определения данной функции будет множество решений неравенства x2 + 5x − 6 ≥ 0 . Неравенство решается методом интервалов. Решим квадратное уравнение x2 + 5x − 6 = 0 . Корни этого уравнения равны

На рисунке область допустимых значений x заштрихована.

Ответ. x (−∞;−6] [1;+∞) .

Элементарные функции. Если в области определения функции бесконечно много значений x , то построить график такой функции весьма затруднительно. Однако существует стандартный набор основных элементарных функций, поведение которых хорошо изучено. К таким функциям относят:

– логарифмическая y = loga x , где a > 0, a ≠1;

– тригонометрические y = cos x, y = sin x, y = tgx, y = ctgx ;

– обратные тригонометрические y = arccos x, y = arcsin x, y = arctgx, y = arcctgx.

Графики этих функций можно найти в справочнике по высшей математике [2]. Элементарными функциями называются функции, которые построены из основных элементарных функций с помощью алгебраических операций и операции взятия функции от функции y = f (x) .

При построении графиков функций с помощью элементарных функций необходимо пользоваться следующими правилами преобразования графиков:

k

раз при 0 < k <1.

5. График функции y = − f (x) получается из графика функции y = f (x)

путём симметричного отражения относительно оси Ox .

6. График функции y = f (−x) получается из графика функции y = f (x) путём симметричного отражения относительно оси Oy .

Пример. С помощью преобразования графиков элементарных функций построить график функции y = −log2 (x +3) .

Решение. Строим график элементарной логарифмической функции y1 = log2 x . График функции y2 = log2 (x +3) получаем путем сдвига графика функции y1 по оси Ox на 3 единицы влево. График функции y3 = −log2 (x +3) получаем из графика функции y2 путём симметричного отражения относительно оси Oy .