
umm_201
.pdf
Если на интервале (a;b)вторая производная положительна f ′′(x) > 0, то график функции является выпуклым вниз. И наоборот, если на интервале (a;b) вторая производная отрицательна, то график функции является выпук-
лым вверх.
Точки, при переходе через которые вторая производная меняет знак, то есть график функции меняет направление выпуклости, называют точками
перегиба.
Итак, исследование функции состоит из следующих этапов:
1)нахождение области определения функции;
2)нахождение точек пересечения графика с осями координат Ox и Oy;
3)нахождение критических точек, промежутков монотонности, точек экстремума функции;
4)нахождение интервалов выпуклости и вогнутости, точек перегиба.
Используя проведённые исследования, можно постепенно строить график функции.
Пример. Провести исследование и построить график функции y = 1 +1x2 .
Исследование. 1) область определения функции – вся числовая прямая, то есть x (−∞;+∞) . Точек разрыва нет и нет вертикальных асимптот.
2) находим точки пересечения с осями координат:
с осью Oy график пересекается, если x = 0 , откуда y =1, то есть M (0;1) – точка пересечения с осью Oy . Нарисуем точку M (0;1) .
С осью Ox график пересекается, если y = 0 , то есть нужно решить уравнение
1 2 = 0. Поскольку это уравнение не имеет решений, то точек пересечения с
1 + x
осьюOx нет. Кроме того, понятно, что y > 0 на всей области определения. Таким образом, точка M (0;1) – единственная точка пересечения графика с осью
Oy .
3) Найдём критические точки. Выражение производной y |
′ |
|
|
2x |
|
|
= − (1 |
+ x2 )2 |
. При- |
||||
|
||||||
равниваем производную к нулю y′ = 0 x = 0 – единственная критическая точка. Она разбивает область определения на два интервала.
|
|
|
|
x |
−∞; 0 |
0 |
0; + ∞ |
|
|
|
|
y′ |
+ |
0 |
– |
|
|
|
|
y |
|
1 |
|
|
|
|
|
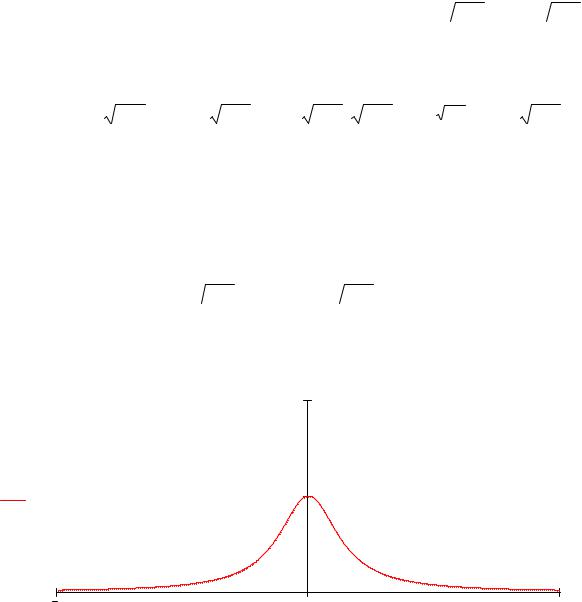
Поскольку в точке (0;1) производная меняет знак с «+» на «-», то точка M (0;1)
является точкой максимума функции. Нанесем эту информацию на чертеже. 4) найдём точки перегиба функции. Вторая производная имеет вид:
|
|
|
x |
|
|
|
′ |
|
1 (1 + x |
2 |
) |
2 |
− x 2(1 + x |
2 |
) 2x |
|
3x |
2 |
−1 |
|
|
|||||||
y |
′′ |
|
|
|
|
|
= −2 |
|
|
|
= 2 |
|
|
|||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
2 |
|
3 . |
При- |
|||||||
|
= −2 |
(1 + x |
) |
|
|
|
|
(1 + x |
) |
|
|
(1 |
+ x |
) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
равнивая к нулю вторую производную, получим x = − 1/ 3 , x =
1/ 3 , x =  1/ 3 . Эти точки разбивают область определения на три интервала, внутри которых характер выпуклости не меняется.
1/ 3 . Эти точки разбивают область определения на три интервала, внутри которых характер выпуклости не меняется.
x |
−∞; − 1/ 3 |
− 1/ 3 |
− 1/ 3; 1/ 3 |
1/ 3 |
1/ 3;+∞ |
|
|
|
|
|
|
y′′ |
+ |
0 |
– |
0 |
+ |
|
|
|
|
|
|
y |
|
0,75 |
∩ |
0,75 |
|
|
|
|
|
|
|
Итак, точки перегиба (− 1/ 3;0,75) и (−
1/ 3;0,75) и (− 1/ 3;0,75) . Нарисуем точки и уточ-
1/ 3;0,75) . Нарисуем точки и уточ-
ним график.
Строим график функции.
y=1/(1+x*2)
2
y(x)
1
7 |
0 |
7 |
x

Понятие дифференциала функции. Производная функции y = f (x) по оп-
ределению есть предел отношения приращения функции |
y к приращению ар- |
||||||||
гумента x при стремлении |
x к нулю |
|
|
y |
|
|
|||
|
|
|
f |
′ |
|
|
. |
|
|
|
|
|
(x) = lim |
|
x |
|
|||
|
|
|
|
|
→0 |
|
|
|
|
При достаточно малых значениях |
x верно приближённое значение равенства |
||||||||
|
|
|
|
′ |
≈ |
y |
, |
|
|
|
|
|
|
f (x) |
x |
|
|
||
Откуда получается приближённая формула приращения функции |
|||||||||
|
|
y ≈ |
|
′ |
x . |
|
|
|
(6.1) |
|
|
f (x) |
|
|
|
||||
Выражение |
в правой части |
равенства |
(6.1) |
называется |
дифференциалом |
||||
функции |
f (x) и обозначается |
dy . Таким образом, по определению имеем |
|||||||
|
dy = |
′ |
|
|
|
|
|
(6.2) |
|
|
f (x) x |
|
|
|
|||||
Полезность этого равенства определяется тем, что часто дифференциал функции вычислить легче, чем приращение. Например, требуется вычислить
значение функции y = x4 в точке x = 2,03. Дифференциал по формуле (6.2) ра-
вен dy = 4x |
3 |
x . Следовательно, |
y |
≈ |
′ |
|
|
f |
(x) x . |
||||
Тогда y(2) =16, здесь x0 = 2 , |
|
а |
приращение аргумента равно |
|||
x= 2,03 − 2 = 0,03, приращение функции равно
y≈ dy = 4 23 0,03 = 32 0,03 = 0,96 .
Следовательно, y(2,03) = y(2) + |
y ≈ y(2) + dy =16,96 . |
|
Для независимой переменной x примем, что dx = |
x . Это позволит ра- |
|
венство (6.2) переписать в виде |
|
|
dy = |
′ |
(6.3) |
f (x) dx . |
||
Так для функции y = sin(2x) дифференциал равен dy = 2 cos(2x)dx .
Равенство (6.3) позволяет рассматривать производную как отношение двух дифференциалов f ′(x) = dydx .
7. Неопределенный интеграл
Неопределённый интеграл. Сформулируем задачу, обратную дифференцированию: для функции f (x) найти такую функцию F(x) , для которой
выполняется F′(x) = f (x) . Такая функция F (x) называется первообразной
для функции f (x) .
Задача отыскания первообразной решается неоднозначно, так как, если F′(x) = f (x) , то это выполняется и для функций
(F(x) +C)′ = f (x) ,
где C – любая постоянная величина. То есть F(x) +C также первообразная для
f (x). Например, для y = 2x функции F1(x) = x2 и F2 (x) = x2 + 2 являются первообразными.
Определение. Если функция F(x) является первообразной от функции
f (x), то выражение F (x) +C называется неопределённым интегралом от
функции f (x) и обозначается символом ∫ f (x) dx . Из определения следует ∫ f (x) dx = F (x) +C . Например, ∫cos x dx = sin x +C .
Основные свойства неопределённого интеграла:
1) производная любой первообразной равна подынтегральной функции
(∫ f (x) dx)′ = f (x) .
2)∫( f (x) ± g(x)) dx = ∫ f (x) dx ± ∫ g(x) dx .
3)∫k f (x)dx = k ∫ f (x) dx .
Вытекающее из определения свойство 1) позволяет проверять путём дифференцирования правильность результата интегрирования. Для нахождения первообразной будем пользоваться следующей таблицей интегралов.
ТАБЛИЦА ИНТЕГРАЛОВ
1. |
∫ x |
α |
dx = |
xα +1 |
|
+C, α ≠ −1 |
2. ∫ |
1 |
dx = ln |
|
x |
|
+C , |
|||||||
|
|
|||||||||||||||||||
|
α +1 |
x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
∫sin x dx = cos x +C, |
4. |
∫cos x dx = −sin x +C, |
|||||||||||||||||
5. |
∫tg x dx = −ln |
|
cos x |
|
+C, |
6. |
∫ctg x dx = ln |
|
sin x |
|
+C, |
|||||||||
|
|
|
|
|||||||||||||||||
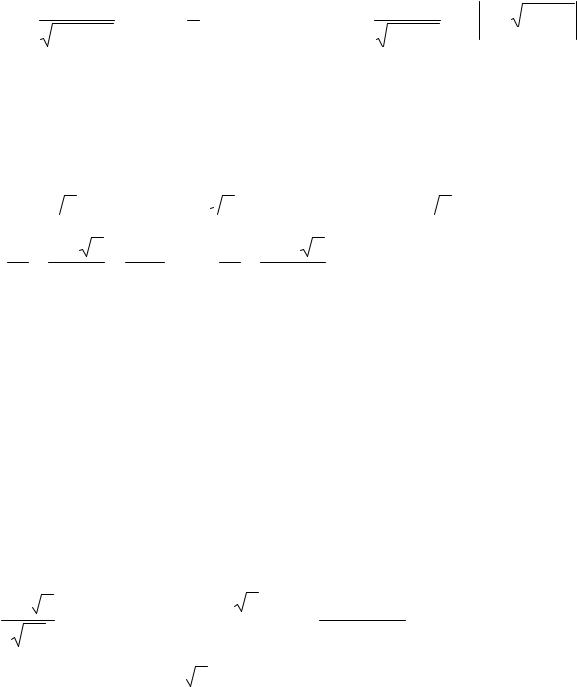
7. |
∫ |
|
dx |
|
= tg x +C, |
|
|
|
8. |
∫ |
|
|
dx |
|
= −ctg x +C, |
|
|
|||||||||||||
cos2 |
|
|
|
|
|
sin2 |
|
|
|
|||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
9. |
∫ex dx = ex +C , |
|
|
|
10. |
|
|
∫ax dx = |
|
ax |
|
+C , |
|
|
||||||||||||||||
|
|
|
|
|
|
ln a |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
11. |
∫ |
dx |
= |
1 |
arctg |
x |
+C , |
12. |
∫ |
dx |
|
= |
1 |
|
ln |
|
|
a + x |
|
|
+C , |
|||||||||
|
|
|
||||||||||||||||||||||||||||
a2 + x2 |
|
|
a2 − x2 |
2a |
a − x |
|||||||||||||||||||||||||
|
|
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
13. |
|
∫ |
a |
dx |
|
= arcsin x |
+C , |
14. |
|
∫ |
dx |
|
= ln x + x2 + a +C . |
|||||||||||||||||
|
|
|
2 − x2 |
|
|
a |
|
|
|
|
|
x2 + a |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Часто задача отыскания первообразной от данной функции решается сведением интеграла к сумме табличных интегралов путем несложных алгебраических преобразований.
Пример. Найдем первообразную для интеграла
∫(x − 4 x)2 dx = ∫(x2 −8x
x)2 dx = ∫(x2 −8x  x +16x)dx = ∫ x2dx − ∫8x
x +16x)dx = ∫ x2dx − ∫8x xdx + ∫16xdx =
xdx + ∫16xdx =
= x3 |
− |
8x2 x |
+ |
16x2 |
+C = x3 |
− |
16x2 x |
+8x2 +C . |
3 |
|
2,5 |
|
2 |
3 |
|
5 |
|
Интегрирование методом замены переменной. Если функция x =ϕ(t) имеет непрерывную производную и монотонна, то в интеграле ∫ f (x)dx можно перейти к новой переменной t по формуле
′ |
(7.4) |
∫ f (x) dx = ∫ f (ϕ(t)) ϕ (t) dt , |
затем найти интеграл из правой части равенства (если это возможно) и вернуться к исходной переменной.
Следует отметить, что в равенстве (7.4) ϕ′(t)dt = dx . Таким образом метод состоит в том, что x заменяют на ϕ(t) , а dx на ϕ′(t)dt .
Пример. Проиллюстрируем метод замены переменной на примере
|
sin |
3 |
x dx = |
|
3 |
, |
t = |
3 |
x |
|
= |
|
sin t 3t |
2 |
dt = 3 sin t dt = |
∫ |
|
x = t |
|
|
|
∫ |
|
||||||||
3 x2 |
|
dx = 3t 2dt, |
|
|
|
|
t 2 |
|
∫ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
== −3cos t +C = −3cos 3 x +C .
Часто приходится замену переменной делать иначе: заменять некоторое алгоритмическое выражение u(x) = t . При этом необходимо заботиться о том,

чтобы x однозначно определялась из этой замены. Рассмотрим еще несколько примеров нахождения первообразной функции.
Примеры.
1. ∫(3x + 2)10 dx можно заметить, что этот интеграл похож на первый таблич-
ный интеграл. Поскольку dx = d (13 3x) = 13 d (3x) = 13 d (3x + 2) , то, подставив в исходный интеграл полученное выражение дифференциала, получим
|
|
|
|
10 |
|
10 |
1 |
|
|
|
|
1 |
10 |
|
1 |
|
|
10 |
|
|
|
∫(3x + 2) dx = ∫(3x |
+ 2) |
|
|
d (3x + 2) |
= |
|
∫(3x + 2) d (3x + 2) |
= |
|
|
∫u |
|
du |
= |
|||||||
3 |
3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
= |
1 |
|
|
(3x + 2)11 |
+C = |
|
(3x + 2)11 |
+C |
|
|
|
|
|
|
|
|
|
|
|||
3 |
11 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. ∫sin(x ± a)dx = ∫sin(x ± a)d (x ± a) = −cos(x ± a) +C .
|
|
Вообще для любой постоянной a верно равенство dx = d (x + a), а так |
|||||||||||||||||||||||||||||||||||
же для любой постоянной k справедливо d (kx ± a) |
= |
1 |
dx . |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||
|
|
Введение функции под знак дифференциала. |
|
Этот прием основан на ра- |
|||||||||||||||||||||||||||||||||
венствах типа |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x dx = |
d (x2 ), |
|
cos x dx = d (sin x), |
ex dx = d (ex ), |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x2dx = |
1 |
d (x3 ), |
|
sin x dx = −d (cos x), |
|
1 |
dx = d (ln x). |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||
|
|
Примеры. Рассмотрим примеры интегралов, в которых используется |
|||||||||||||||||||||||||||||||||||
введение функции под знак дифференциала. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1. |
∫ |
tdt |
|
= |
1 |
|
∫ |
dt 2 |
|
= |
1 |
∫ |
d (t 2 +1) |
|
= |
|
1 |
ln(t 2 +1) +C , |
|
||||||||||||||||||
|
|
2 |
|
t 2 + |
|
2 |
|
2 |
|
||||||||||||||||||||||||||||
|
|
t 2 +1 |
|
|
1 |
|
|
|
|
|
t 2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2. |
∫sin x cos |
2 |
x dx |
= −∫cos |
2 |
x d cos x |
|
= − |
cos3 |
x |
+C , |
|
|||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
∫cos(ex +1)exdx = ∫cos(ex +1) dex |
= ∫cos(ex +1)d (ex +1) = sin(ex +1) +C , |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3x −1 = t, dx = |
2tdt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4. |
∫ |
|
dx |
|
|
|
|
|
|
|
|
|
= |
2 |
∫ |
|
tdt |
|
= 2 ∫ |
(t +3) −3dt = |
|||||||||||||||||
|
|
3 |
= |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||||||||||
|
|
3x −1 + |
|
|
|
|
|
(t |
2 |
|
|
|
|
|
|
|
|
3 |
|
t +3 |
3 |
t +3 |
|||||||||||||||
|
|
|
|
|
|
|
|
x = |
3 |
|
|
+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
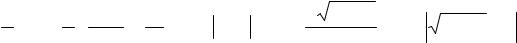
= |
2 |
∫dt − |
2 |
∫ |
3dt |
= |
2t |
− 2 ln t +3 +C = |
2 3x −1 |
− 2 ln 3x −1 +3 +C . |
|
3 |
|
3 |
|
t +3 |
|
3 |
|
3 |
|
Метод интегрирования по частям. Метод интегрирования по частям применяется преимущественно для интегралов вида:
∫ xk sin xdx, ∫ xk cos xdx, ∫ xk ex dx, ∫ xk ln xdx ,
∫arcsin x dx, ∫arccos x dx, ∫arctgx dx .
Формулой интегрирования по частям называется равенство
∫u dv = u v − ∫v du , |
(7.5) |
где u = u(x), v = v(x) – дифференцируемые функции.
Рассмотрим несколько примеров, иллюстрирующих применение этой формулы.
u = x, du = dx, 1. ∫ x sin xdx = dv = sin xdx, v
= −x cos x +sin x +C .
= −x cos x + ∫cos xdx = = −cos x
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
u = ln(x +1), |
du |
= |
|
|
, |
|
x2 |
|
x2 |
|
dx |
|
|
|||
x +1 |
|
|
|
|
|
|||||||||||
2. ∫ x ln(x +1)dx = |
|
|
x2 |
|
|
|
|
|
= |
|
ln(x +1) − ∫ |
|
|
|
|
= |
|
|
|
|
|
|
2 |
2 |
x + |
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dv = x dx, |
v = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
1 |
|
(x2 −1) +1 |
|
|
x2 |
|
|
|
|
|
|
1 |
|
(x −1)(x +1) |
|
||||||||
= |
|
|
|
ln(x +1) − |
|
∫ |
|
|
|
|
|
dx = |
|
|
|
|
ln(x +1) − |
|
∫ |
|
dx − |
||||||||||
2 |
2 |
x +1 |
|
|
|
|
2 |
|
2 |
x +1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
− |
1 |
∫ |
|
dx |
|
= |
x2 |
ln(x +1) − |
1 |
|
(x −1) |
2 |
|
− |
1 |
ln |
|
x +1 |
|
+C . |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
x + |
1 |
2 |
2 |
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8. Определенный интеграл
Понятие определенного интеграла. Пусть функция y = f (x) определена на отрезке [a, b]. Разобьем отрезок произвольным образом точками
a = x0 < x1 < x2 <K< xn = b
на n частичных отрезков. Длина каждого отрезка равна xi = xi − xi −1 , 1 ≤ i ≤ n .
Выберем в каждом из них произвольную точку ci , xi −1 ≤ ci ≤ xi .
Сумма, составленная из n слагаемых
Sn = f (c1) x1 + f (c2 ) x2 +K+ f (ci ) xi +K+ f (cn ) xn ,
называется n -ой интегральной суммой функции y = f (x) на отрезке [a, b]. Для сокращения записи используется математический знак суммы
n |
xi . |
|
|
Sn = ∑ f (ci ) |
|
|
|
i =1 |
f (x) ≥ 0 , то число Sn представляет собой сумму площадей прямо- |
||
Если |
|||
угольников, с основаниями |
xi и высотами, равными f (ci ) . |
||
Определённым интегралом от функции y = f (x) на отрезке [a, b] |
|||
называется предел интегральной суммы Sn |
при стремлении к нулю максималь- |
||
ной длины частичных отрезков. |
f (x) на отрезке [a, b] обозначается |
||
Определённый интеграл от функции |
|||
b
∫ f (x) dx .
a
Согласно этому определению можно записать
b |
lim Sn . |
|
∫ f (x) dx = |
(8.1) |
|
a |
max xi →0 |
|
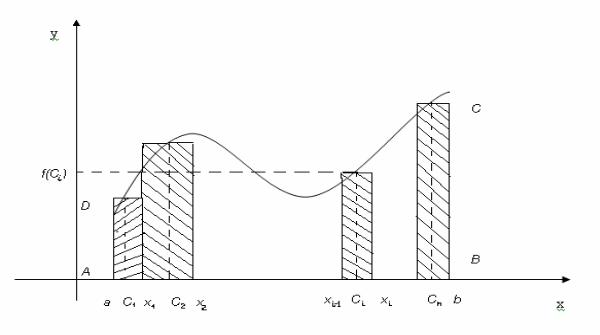
Рис. 5. Определенный интеграл
Вформуле (8.1) отрезок [a, b] называется отрезком интегрирования,
ачисла a и b называются соответственно нижним и верхним пределами интегрирования. Переменная x называется переменной интегрирования.
Задача о вычислении площади криволинейной трапеции. Пусть f (x) ≥ 0 на отрезке [a, b] (см. рисунок 5.). Фигура АВСД, снизу ограниченная осью Ox , сверху графиком функции y = f (x) и прямыми x = a, x = b, называ-
b
ется криволинейной трапецией. Определённый интеграл ∫ f (x) dx равен
a
площади криволинейной трапеции АВСД.
Основные свойства определенного интеграла. Пусть функции f (x) и g(x) интегрируемы на рассматриваемых отрезках. Тогда выполняются следующие свойства для интегралов:
|
b |
|
b |
b |
1. |
∫( f (x) ± g(x)) dx = ∫ f (x) dx ± ∫ g(x) dx , |
|||
|
a |
|
a |
a |
|
b |
|
b |
|
2. |
∫k f (x) dx = k ∫ f (x) dx , |
(k = const) . |
||
|
a |
|
a |
|
|
b |
|
a |
|
3. |
∫ f (x) dx = − ∫ f (x) dx . |
|
||
|
a |
|
b |
|
|
b |
c |
b |
|
4. |
∫ f (x) dx = ∫ |
f (x) dx + ∫ f (x) dx , где c (a;b) . |
||
|
a |
a |
c |
|

Формула Ньютона-Лейбница. Если F (x) – какая-либо первообразная функции f (x), то справедлива формула Ньютона-Лейбница
b |
ba = F (b) − F (a) . |
|
∫ f (x) dx = F(x) |
(8.2) |
|
a |
|
|
Эта формула сводит задачу вычисления определенного интеграла к отысканию первообразной, то есть к вычислению неопределенного интеграла.
e |
ln2 |
e |
ln3 x |
e |
ln3 e |
|
ln3 1 |
|
3 |
|
|
|||
Пример. ∫ |
|
dx =∫ln2 x d (ln x) = |
|
|
1 = |
|
− |
|
|
= |
|
|
−0 |
=1. |
x |
3 |
3 |
3 |
|
3 |
|||||||||
1 |
1 |
|
|
|
|
|
|
|
||||||
b |
Замена переменной в определенном интеграле. |
Если дан |
интеграл |
||||
f (x)dx , то при замене x =ϕ(t) нужно заменить не только x на ϕ(t) |
и dx на |
||||||
∫ |
|||||||
a |
′ |
|
|
a и b , согласно следующей |
|||
ϕ (t)dt , но и поменять пределы интегрирования |
|||||||
формуле |
|
|
|
|
|
||
|
|
′ |
|
|
|
|
|
|
b |
x =ϕ(t), dx =ϕ (t) |
dt |
β |
′ |
|
|
|
∫ |
|
|
||||
|
f (x)dx = |
= ∫ f (ϕ |
(t)) ϕ (t)dt . |
|
|||
|
a |
a =ϕ(α), b =ϕ(β) |
|
α |
|
|
|
После вычисления интеграла не нужно возвращаться к прежней переменной x , так как пределы интегрирования меняются с учетом замены переменной.
|
|
3 |
x dx |
|
|
|
|
+ x = t |
2 |
, x |
= t |
2 |
−1, |
|
dx = 2t |
dt |
|
2 |
2t(t |
2 |
−1) dt = |
||||||||||
Пример. ∫ |
= |
1 |
|
|
|
|
= ∫ |
t |
|||||||||||||||||||||||
|
|
0 |
x +1 |
|
|
при |
|
|
x = 0 |
t =1, при x = 3 t = 2 |
1 |
|
|
||||||||||||||||||
2 |
2 |
|
|
t |
3 |
|
|
|
|
2 |
|
|
8 |
|
|
1 |
|
8 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= 2∫(t −1)dt = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
= 2 |
− 2 − 2 |
−1 = |
|
|
. |
|
|
|
|
|
|||||||||||||||
|
|
|
−t |
|
3 |
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
||||||||||
Приближенное вычисление определенного интеграла. Довольно часто возникают ситуации, когда определенный интеграл невозможно вычислить по формуле Ньютона-Лейбница. В этих случаях интеграл можно вычислить приближенно, например, по формуле прямоугольников или по формуле трапеций. Рассмотрим методы приближенного вычисления по этим формулам.
1.Метод прямоугольников. Разобьем отрезок [a;b] на n равных частей
длины h = b −n a следующим образом
a = x0 < x1 < x2 <K< xn = b ,
