
umm_201
.pdf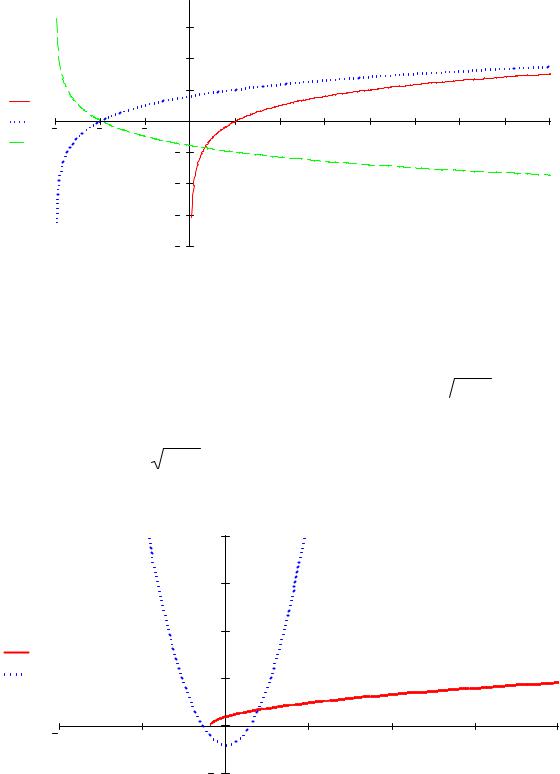
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
y1(x) |
|
|
|
2 |
|
|
|
|
|
|
|
|
y2(x) |
|
|
|
|
|
|
|
|
|
|
|
|
y3(x) |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
Рис.1. Построение графика функций с помощью преобразований |
|||||||||||
Пример. Решить графически уравнение x2 − 2 =  x +1.
x +1.
Решение. |
Графическим решением уравнения называются абсциссы точек пе- |
|
ресечения |
двух графиков |
функций. Построим графики двух функций |
y2 = x2 − 2, y1 = x +1 . |
Графики данных функций пересекаются в одной |
|
точке, следовательно, данное уравнение имеет единственный корень – абсциссу точки пересечения x0 = 2,76.
20
15
10
y1 ( x)
y2 ( x)
5
10 |
|
5 |
0 |
5 |
10 |
15 |
20 |
|
5
x
Рис. 2. Графический способ решения уравнения
Ответ. Корень уравнения x0 = 2,76.

Задания для контрольной работы №1
1-10. Решить уравнения |
|
|
||||||||||||||||||||||||||||||||||||||
1. |
а) |
x |
|
− |
2 |
|
|
|
|
|
= |
|
x |
+ |
|
|
4 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2. |
а) |
2 |
|
|
|
|
+ |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
= 0,625 , |
|
|||||||||||||||
x − 4 |
|
x2 − 4x |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3. |
а) |
|
|
|
|
2 |
|
|
|
|
|
+ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
=1, |
|
|
|
|
||||||||||
|
x + |
2 |
|
|
|
x |
− |
2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4. |
а) |
x −3 |
|
= |
|
4(x +3) |
, |
|
|
|
|
|
|
|||||||||||||||||||||||||||
x +3 |
|
|
|
|
|
|
x −3 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
5. |
а) |
|
2 |
− |
|
|
2x −3 |
|
|
= |
|
|
|
|
|
|
|
|
|
−12 |
, |
|||||||||||||||||||
|
x |
|
x2 −5x |
|
x2 −10x + 25 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
6. |
а) |
|
|
|
|
10 |
|
|
|
|
|
|
− |
|
|
20 |
|
|
|
|
|
= |
1 |
, |
|
|||||||||||||||
10 − x |
|
x +30 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||||||||||||||||||||||
7. |
а) |
|
|
|
|
x |
|
|
|
|
+ |
|
|
|
|
|
|
x |
|
|
|
|
|
= |
|
|
8 |
, |
|
|
|
|
||||||||
|
x − |
5 |
|
|
|
x |
+ |
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||
8. |
а) |
|
|
|
|
5 |
|
|
|
|
|
|
|
+ |
|
|
|
12 |
|
|
|
|
|
=1, |
|
|||||||||||||||
17 − x |
17 + x |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
9. |
а) |
|
2x +1 |
|
+ |
|
2x −1 |
|
= 5,2, |
|
||||||||||||||||||||||||||||||
|
2x −1 |
2x +1 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
10. |
а) |
|
|
x − 2 |
+ |
x + 2 |
|
= |
10 |
|
, |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
x + 2 |
|
|
|
|
|
x − 2 |
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||
б) |
x − 4 −3 = x −13 . |
б) |
2x +3 − 4 − x = 2 . |
б) |
x2 − 2x −12 = 6 . |
б) |
x −1 + x +3 = 2. |
б) |
2x2 + x −39 = x −1. |
б) |
− 2x2 −7x +3 = x −1. |
б) |
−3x + 7 = x + 7 . |
б) |
15 +3x =1 − x . |
б) |
x + x −3 = 3. |
б) |
4x2 − 29x + 23 = 4 . |
11-20. Выполнить действия с заданными матрицами
11. |
|
2 1 |
1 |
−1 |
12. |
3 |
5 |
2 1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 2 |
|
|
2 |
|
|
|
4 |
−1 |
|
|
−3 2 |
|
|
|
|
1 |
|
|
|
|
|
||||||
13. |
− 4 1 2 |
|
|
14. |
|
3 |
2 2 |
|
|
|||||
|
8 3 |
|
|
|
|
− 4 − 2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
− 2 |
|||||
15. |
|
5 3 |
1 6 |
|
16. |
|
4 9 |
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 4 |
|
|
|
−1 7 |
|
|
|
6 |
−8 |
|
|
1 0 |
|
|
|
|
|
|
|
|
|||||
17. |
|
−3 9 2 |
|
18. |
|
− 4 6 2 |
|
|
|
|
||||
|
|
|
|
|
|
− 2 7 |
|
|
|
|
|
|
||
|
|
−5 7 |
|
|
|
|
|
|
|
|
|
|
||

|
5 |
2 |
1 |
|
1 |
6 |
|
|
1 7 0 |
|
|
|
2 |
6 |
|
|
||||
19. |
|
|
2 |
4 |
|
20. |
|
|
0 |
4 |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
9 |
0 |
2 |
|
|
|
|
|
|
2 5 5 |
|
|
|
|
|
||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
3 |
0 |
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
21-30. Найти решение системы линейных уравнений методом Крамера
|
2x − y + 2z = −2, |
||
21. |
|
x + y + |
z = 2, |
|
|||
|
|
x + |
2z = −1. |
|
|
||
=9,
23.− x + y + 2 z = −4,x − = 1.3y − z4 y −3z2x +
3x + 2 y − z = 5, |
||
|
x + |
3z = −3, |
25. |
||
|
x − 2 y |
= −4. |
|
||
−2z 4,
27.− x − y +3z = −5,
y + z 1.
==4x + y
−+3z
29.x − y + 2z =1,x + y + z = 3.= 3,2x y
+y + 2z
3y − z = −5,
x + 2 y + 8.= 7,3z =x
2x − y +3z = |
5, |
||
|
x − y − |
z = −9, |
|
24. |
|||
|
y + |
z = |
7. |
|
|||
x + y + 4z =10,
26.− x − 2 y + z = −1,2x − 2 y + 3z = 6.
|
2x +3y − |
z =3, |
||
28. |
|
|
z =3, |
|
4 x + |
||||
|
|
x − y −3z = 4. |
||
|
|
|||
|
|
x − 2 y + z = |
4, |
|
30. |
|
x + y + 2z = |
0, |
|
|
||||
|
|
|
z = −5. |
|
|
− x + y + |
|||
31-40. С помощью преобразования графиков основных элементарных функций построить графики функций
31. |
а) |
y = 2 sin(π − x); |
|
б) |
y = − |
1 |
|
|
+3 . |
||||||
|
x −1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|||||
32. |
а) |
y = 0.5 x +1 − 4 |
; |
б) |
|
|
|
− |
|
||||||
y = tg x |
4 |
+1. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
33. |
а) |
y = 2 −ln(x +3) ; |
|
б) |
y = |
|
2 |
|
−1. |
|
|||||
|
x |
−1 |
|
||||||||||||
|
|
|
|
π |
|
|
|
|
|
|
|
||||
34. |
а) |
+ |
б) |
y = 2 |
1 − x +1. |
||||||||||
y = 0.5 cos x |
3 |
; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
π |
−1; |
б) y = 2(x −1) |
3 |
−1. |
35. а) y = sin x + |
|
|
|||
|
4 |
|
|
|
|
36. а) y = |
2 |
|
π |
|
||
|
+ 0.5 ; |
б) y = 2ctg |
|
− x . |
||
x + 0.5 |
3 |
|||||
|
|
|
|
|||
37. |
а) |
y = 2x−1 + 4; |
|
|
|
|
|
|
|
|
|
|
б) |
y = 3 − |
|
|
|
2 |
|
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
−1 |
|
|
|
|
|
|||||||||||||||||||
|
|
y = 31−x + 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
38. |
а) |
|
|
|
|
|
|
|
|
|
|
б) |
y = 4 + log2 (x + 2) . |
|
||||||||||||||||||||||
39. |
а) |
y = 3 −(x + 2) |
3 |
; |
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
+1. |
||||||||
|
|
|
|
|
|
|
|
y = 2 cos |
|
|
|
− x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
40. |
а) |
y = 3 −3x+2 |
|
|
|
|
|
|
|
|
|
|
б) |
y = 4 − 2 |
x −0.5 . |
|
|
|||||||||||||||||||
41-50. |
Найти области определения для функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
41. |
а) |
y = |
− x2 + 2x +3 + ln(x − 2) ; |
б) |
y = |
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||
|
x2 |
|
− 4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
42. |
а) |
y = |
x2 −5x −6 + |
|
x ; |
б) |
y = |
|
|
|
|
2 |
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 − x |
|
|
|
|
|
|
|
|
|
||||||
43. |
а) |
y = lg(x2 − 4) + |
x +3 ; |
б) |
y = |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
. |
|
|
|
|||||||||||||
|
x2 |
|
−5x + 6 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
ln(x − 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||
44. |
а) |
y = |
; |
|
|
|
|
|
|
|
|
|
б) |
y = |
|
|
|
9 − x2 |
+ |
|
|
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x −1 |
|
|
|||||||||||||||||||||
|
|
|
x − 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
||||||
45. |
а) |
y = |
|
|
|
|
|
|
+ lg(1 − x) ; |
б) |
y = 3 |
x −2 |
+ |
|
|
|
|
|
||||||||||||||||||
|
|
|
x2 +10x +9 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|||||||||
46. |
а) |
y = |
x2 +3x − 40 + |
; |
|
б) |
y = ln(x −1)+ |
|
|
|
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − x |
|
||
47. |
а) |
y = lg(4x2 −3x − 22) ; |
|
|
|
б) |
y = |
|
|
|
|
2 |
|
|
|
|
+ |
|
1 |
. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − |
|
4 |
|
|
|
x + 4 |
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
48. |
а) |
y = |
+ |
|
|
7 − x ; |
|
|
|
|
б) |
y = 2 |
x |
+ |
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
x2 −9 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 −6x +8 |
|||||||||
49. |
а) |
y = lg(−x2 +8x) + |
|
|
|
|
; |
б) |
y = ln(x + 2) −ln(4 − x) . |
|||||||||||||||||||||||||||
|
x − 2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
50. |
а) |
y = ln(x2 −1) + |
|
; |
|
|
|
|
б) |
y = |
|
|
|
|
|
|
|
|
|
− |
|
|
10 − x . |
|||||||||||||
|
x − |
5 |
|
|
|
|
x |
2 |
|
+ 4x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||

51-60. Решить графически уравнение |
|
|
||||
51. |
2x + x −5 = 0 . |
56. |
log2 (x + 2) + x −3 = 0 . |
|||
52. |
2 −ex + x = 0 . |
57. |
2−x −3x +1 = 0 . |
|||
53. |
|
x −1 + 4 − x = 0 . |
58. |
2x −1 − x = −3 . |
||
54. |
sin 2x − x +1 = 0. |
59. |
x − x2 +3 = 0 . |
|||
55. |
|
1 |
|
+ x2 = 0 . |
60. |
cos x − x + 2 = 0 . |
|
x −1 |
|||||
|
|
|
|
|
||
5. Предел и производная функции
Предел функции. Пусть дана функция y = f (x) . Возможно, при приближении аргумента x к некоторому значению a значения функции f (x) при-
ближаются к какому-то числу b . В этом случае число b называется пределом функции f (x) при x стремящемся к a . Математически это записывается
так |
|
lim f (x) = b . |
(5.1) |
x→a |
|
Например, если f (x) = x +1, то при приближении x к 2 значения функции приближаются к 3. То есть предел данной функции при x , стремящемся к
двум, равен lim(x +1) = 3.
x→2
Если lim f (x) = 0 , то |
f (x) называется бесконечно малой при x → a . |
x→a |
|
Например, функция |
f (x) = x3 −1 – бесконечно малая, при x →1. Воз- |
можен другой случай, когда значения функции неограниченно возрастают по
абсолютной величине, при x → a . В этой ситуации функцию f (x) |
называют |
|||
бесконечно |
большой и записывают lim f (x) = ∞. Например, |
функция |
||
|
1 |
|
x→a |
|
f (x) = |
|
будет бесконечно большой при x →1. |
|
|
x −1 |
|
|||
|
|
|
||
При вычислении пределов функций следует пользоваться основными свойствами пределов:
1) |
lim( f (x) ± g(x)) = lim f (x) ± lim g(x) |
||
|
x→a |
x→a |
x→a |
2) |
lim( f (x) g(x)) = lim f (x) lim g(x) |
||
|
x→a |
x→a |
x→a |
3) lim
x→a
f (x) |
= |
lim f (x) |
, при lim g(x) ≠ 0 . |
|
x→a |
||||
g(x) |
lim g(x) |
|||
|
x→a |
|||
|
|
x→a |
|
Эти свойства применимы только тогда, когда пределы функций f (x) и g(x)
конечны. Если же обе функции являются бесконечно малыми или бесконечно большими, то при вычислении пределов могут потребоваться дополнительные преобразования. Неопределенные ситуации складываются также при делении двух функций, стремящихся к нулю (бесконечно малые функции), при умножении бесконечно малой на бесконечно большую функцию, при возведении функции, значения которой в данном процессе приближаются к единице в бесконечно большую степень.
|
|
Например, |
f (x) = x2 −3x + 2 и g(x) = x2 −5x + 4 бесконечно |
малые |
||||||||||||||||||||||||||||||||
функции при x →1. Вычислим предел их отношения |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
lim |
x2 |
−3x + 2 |
|
= lim |
|
(x − 2)(x −1) |
|
= lim |
x − 2 |
|
= |
|
−1 |
|
= |
|
1 |
|
. |
|
|
|
|
||||||||||||
|
x2 |
−5x + 4 |
|
(x − 4)(x −1) |
x − |
4 |
|
|
−3 |
|
3 |
|
|
|
|
|||||||||||||||||||||
|
x→1 |
x→1 |
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Другой пример. Найти предел |
lim |
x − 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
f (x) = x − 2, |
|
|
|
|
x→∞ |
2x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x → ∞. |
||||||||||||
Здесь |
g(x) = x +1 бесконечно большие функции при |
|||||||||||||||||||||||||||||||||||
Имеет |
место |
неопределённость |
вида |
|
∞ |
. |
Проведём |
преобразование |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x − 2 |
|
|
1 − 2 / x |
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= |
|
(каждое слагаемое разделили на |
x ). Здесь очевидно соотно- |
||||||||||||||||||||||||||||||||
|
|
2 +1/ x |
||||||||||||||||||||||||||||||||||
|
2x +1 |
|
|
|
|
|
|
x − 2 |
|
|
|
1 − 2 / x |
|
|
|
1 −0 |
|
|
|
|
||||||||||||||||
шение lim |
1 |
= 0 . Тогда имеем lim |
|
= lim |
= |
|
= |
1 |
. |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
x→∞ x |
|
|
x→∞ 2x +1 |
x→∞ |
|
|
2 +1/ x 2 + 0 2 |
|
|||||||||||||||||||||||||
|
|
|
Производная функции. Пусть функция y = f (x) |
определена в точке x0 |
||||||||||||||||||||||||||||||||
и принимает значение в этой точке, равное |
y0 |
= f (x0 ). Величина изменения |
||||||||||||||||||||||||||||||||||
аргумента при переходе из точки x0 в какую-либо другую точку x называется приращением аргумента и обозначается x . То есть x = x − x0 и отсюда x = x0 + x . Если аргумент получит приращение, то и значение функции тоже получит соответствующее приращение y = f (x0 + x) − f (x0 ) и примет значение y = y0 + y .
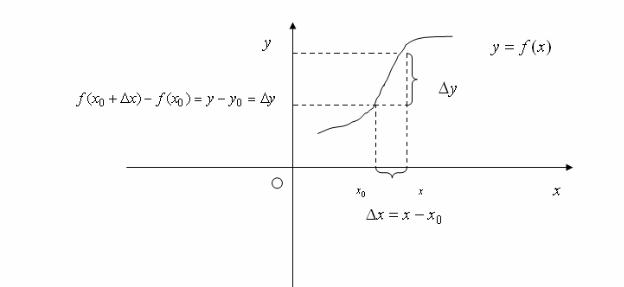
Рис. 3. Приращение функции и приращение аргумента
Определение. Предел отношения приращения функции к приращению
аргумента при x → 0 называется производной функции |
y = f (x) в точке |
|||
x0 и записывается |
|
|
|
|
f ′(x0 ) = lim |
f (x0 + |
x) − f (x0 ) |
. |
(5.2) |
|
|
|||
x→0 |
x |
|
||
Если названный предел существует и конечен, то функция называется дифференцируемой в точке x0 , а операция нахождения производной называет-
ся дифференцированием.
Роль производной определяется, прежде всего, тем, что она характеризует скорость изменения функции. Так, если это путь, который проходит
точка за время t , S′(t) =V (t) – это скорость этой точки в момент времени t . Производная функции y = f (x) в точке x0 также описывает предельное положение секущей к графику этой функции в точке с координатами M 0 (x0 ; y0 ) , то есть касательную. На рис.4 построена касательная к графику функции y = f (x) в точке M 0 (x0 ; y0 ) . Прямая M 0 M – секущая графика функции y = f (x) , расположенная под углом ϕ к сои Ox . Угол α – это угол между касательной и положительным направлением оси абсцисс.
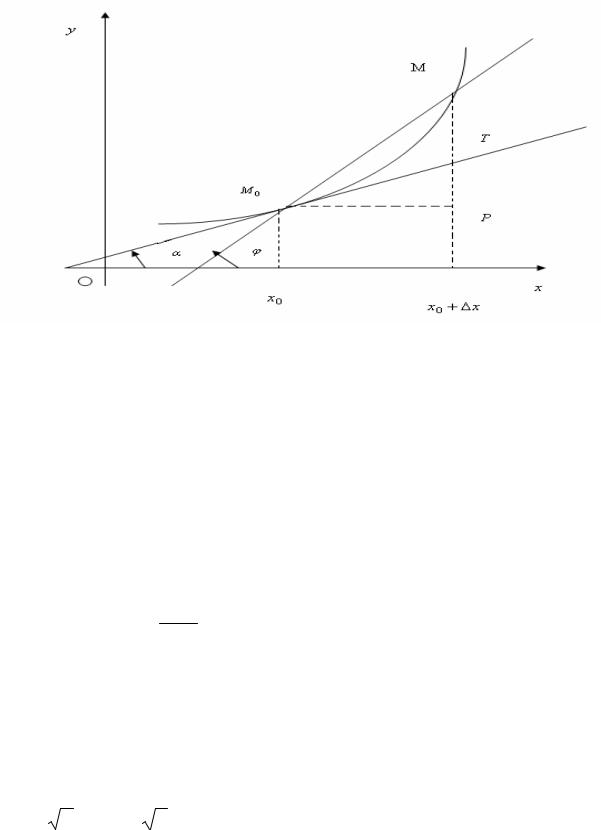
Рис. 4. График касательной к графику функции y = f (x) в точке x0
Уравнение касательной к графику функции y = f (x) в точке x0 |
имеет вид |
y = f ′(x0 ) (x − x0 ) + f (x0 ) , |
(5.3) |
где f ′(x0 ) = tg α .
В дифференциальном исчислении важную роль играет число e , равное приблизительно 2,7182….. Логарифм loge x по основанию e называется нату-
ральным логарифмом и обозначается ln x . Полезна следующая формула, показывающая, что логарифм по основанию a можно выразить через натуральный
логарифм loga x = lnln10x .
ТАБЛИЦА ОСНОВНЫХ ФОРМУЛ ДИФФЕРЕНЦИРОВАНИЯ
1. C |
′ |
= 0 |
2. x |
′ |
=1 |
3. (x |
n |
′ |
= nx |
n−1 |
|
|
) |
|
|
′ |
=1/(2 x) |
1 |
′ |
1 |
|
(e |
x ′ |
= e |
x |
||
5. |
|
|
= − |
|
6. |
|
|||||
4. ( x) |
x2 |
) |
|
||||||||
|
|
x |
|
|
|
|
|
|
|
||
7. (a |
x |
′ |
= a |
x |
ln a |
′ |
= |
1 |
′ |
= |
1 |
|
|
|
|
||||||||
|
) |
|
8. (ln x) |
x |
9. (loga x) |
x ln a |
|||||
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
1 |
|
10. |
(sin x)′ = cos x |
|
|
11. |
(cos x)′ = −sin x |
12. (tg x)′ = |
|
||
|
|
cos2 x |
|||||||
|
1 |
|
|
|
|
1 |
|
|
|
13. |
(ctg x)′ = − |
|
|
14. |
(arcsin x)′ = |
|
|||
sin2 x |
1− x2 |
||||||||
15. |
(arccos x)′ = − |
1 |
16. |
(arctg x)′ = |
1 |
|
|
||
1− x2 |
1+ x2 |
|
|
||||||
17. (arctg x)′ = −1 +1x2
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
|
|
|
|
′ |
= C |
′ |
|
|
|
|
2. ( f (x) ± g |
|
|
′ |
′ |
|
|
′ |
|
|
|
|
|||||||||
1. (Cf (x)) |
f (x) |
|
|
|
(x)) = f |
(x) ± g (x) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
′ |
= |
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. ( f (x) g(x)) |
f (x) g(x) + g (x) f (x) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
′ |
|
′ |
|
|
′ |
|
|
|
|
f (x) |
|
|
f (x) g(x) − f (x) g (x) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4. |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. ( f (g(x)) |
|
= f (g(x)) |
g (x) |
||||||||||||
|
|
|
|
|
|
(g(x))2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Последнее правило называется дифференцированием сложной функции и |
||||||||||||||||||||||||||||
занимает наиболее |
важное место |
|
в дифференциальном |
исчислении. Если |
|||||||||||||||||||||||||||
y = f (u) – некоторая функция аргумента u , а |
u = g(x) – другая функция аргу- |
||||||||||||||||||||||||||||||
мента x , то говорят, что y = f (g(x)) сложная функция от x . |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Пример1. Найти производную функции y = cos(x5 ) . |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Здесь |
f (u) = cos u , u = g(x) = x5 , тогда, |
используя правило 5 |
диффе- |
|||||||||||||||||||||||||
ренцирования |
|
|
|
и |
основные |
|
формулы |
дифференцирования, |
получим |
||||||||||||||||||||||
y |
′ |
= |
|
′ |
|
|
′ |
= −sin(u) (x |
5 |
|
′ |
|
|
|
|
5 |
) 5x |
4 |
= −5x |
4 |
sin(x |
5 |
) . |
|
|
||||||
|
(cos u)u ux |
|
) = −sin(x |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Пример2. Найти производную функции y = x ln |
|
x . |
|
|
|
|
|
|||||||||||||||||||||
Используем |
сначала |
правило |
дифференцирования |
|
|
3). |
В нашей |
задаче |
|||||||||||||||||||||||
f (x) = x, |
g(x) = ln |
x . Получим y |
′ |
= (x ln |
|
|
′ |
′ |
ln |
x + (ln |
′ |
x = |
|||||||||||||||||||
|
|
x) = x |
|
x) |
|||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
′ |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
=1 ln x + |
|
x |
|
( |
x) |
x = ln |
|
|
x + |
|
x 2 |
|
x x = ln |
x + 2 |
. Здесь |
учитывали, |
|||||||||||||||
что g(x) = ln  x – сложная функция.
x – сложная функция.
6.Исследование функций с помощью производной
Вэтом разделе мы рассмотрим исследование функций и построение их графиков с помощью производной. Введем несколько понятий.
Функция y = f (x) называется возрастающей на интервале (a;b), если при a < x1 < x2 < b выполняется условие f (x1) < f (x2 ) .
Функция y = f (x) называется убывающей на интервале (a;b), если при
a < x1 < x2 < b выполняется условие f (x1) > f (x2 ) . |
|
|||
Если производная f |
′ |
(a;b) положительна, |
то функция на этом |
|
(x) на |
||||
интервале возрастающая. |
Если f |
′ |
y = f (x) убывает на |
|
(x) < 0, то функция |
||||
(a;b). |
f (x0 ) функции y = f (x) называется максимальным, если во |
|||
Значение |
||||
всех точках x , |
близких к |
x0 , выполняется неравенство |
f (x0 ) > f (x) . В этом |
|
случае точка x0 называется точкой максимума функции. |
||||
Значение |
f (x0 ) функции y = f (x) называется минимальным, если во |
|||
всех точках x , |
близких к x0 , выполняется неравенство |
f (x0 ) < f (x) . В этом |
||
случае точка x0 называется точкой минимума функции.
Точки максимума и минимума называются точками экстремума функции. Область определения функции с помощью производной легко разбить на интервалы монотонности. Точка x0 называется критической, если в ней про-
изводная функции не существует или равна нулю.
Критические точки разбивают область определения на интервалы. На каждом промежутке интервала следует проверить знак производной. В зависимости от того, какой знак имеет производная на промежутке, возникают следующие ситуации:
если при переходе через критическую точку x0 производная меняет знак с плюса на минус, то точка x0 – точка максимума функции;
если при переходе через критическую точку x0 производная меняет знак с минуса на плюс, то точка x0 – точка минимума функции;
|
если при переходе через критическую точку x0 |
производная не меняет |
|||
знак, то x0 не является точкой экстремума функции. |
|
||||
|
Производная от производной для функции y = f (x) называется произ- |
||||
водной |
|
второго порядка (или |
второй производной) и обозначается |
||
′ ′ |
= y |
′′ |
′′ |
|
|
( y ) |
|
= f (x). |
′′ |
|
|
|
По знаку второй производной |
можно определить на- |
|||
|
функции f (x) |
||||
правление выпуклости графика функции y = f (x) .
