5.2. Наилучшее приближение в пространстве rn[a; b]. Метод наименьших квадратов

Наилучшие приближения в пространстве ищутся обычно в тех случаях, когда основная информация о приближаемой функции дается в виде таблицы ее значений, а табличные значения имеют значительные погрешности.

Общая схема метод наименьших квадратов

Пусть на заданном отрезке введена сетка точеки известна таблица значений некоторой функциив узлах сетки, а табличные значенияимеют значительные погрешности. В то же время известно, что функциядолжна содержаться в параметрическом семействе функций, заданном формулой

. (5.2.1)

Здесь  параметры, которые могут принимать любые вещественные значения, а  известные функции, образующие линейно независимую систему. Будем искать наилучшее приближение для функции на отрезке.

Искать приближение функции с помощью интерполяции не имеет смысла, так как требование совпадения значений приближающей функции с табличными значениямине обеспечит в описанном случае существенного повышения точности приближения. В то же время целесообразно использовать и дополнительную информацию о функции.

Будем искать приближение для функциив параметрическом семействе функций, заданных формулой (5.2.1). Иными словами, искомое приближение задается формулой

, (5.2.2)

где  некоторые неизвестные нам значения параметров .

Наряду с функциями , будем использовать их сеточные аналоги, то есть функции, определенные только на сетке, со значениями

,

. (5.2.3)

Сеточные аналоги являются сеточными функциями и принадлежат пространству , в котором мы ввели скалярное произведение, норму и метрику по формулам (5.1.4) (5.1.6). При отыскании приближения будем подбирать такие значенияпараметров, чтобы сеточный аналог искомого приближения был наилучшим приближением для сеточного аналогасреди всевозможных функций параметрического семейства (5.2.1) в пространстве :

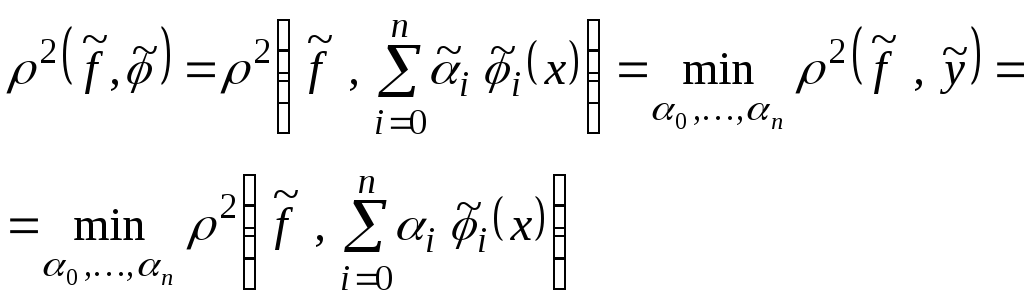(5.2.4)

Минимизируемая величина 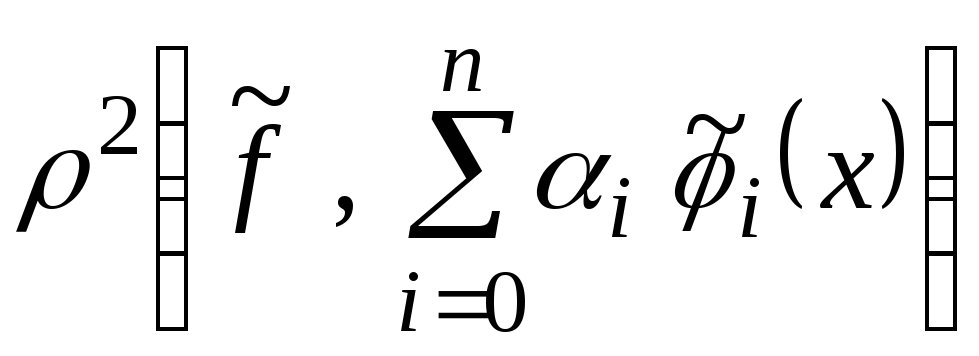представляет собой функцию. Рассмотрим ее подробнее:

. (5.2.5)

Запишем необходимые условия минимума функции .

(5.2.6)

Условия (5.2.6) представляют собой систему линейных алгебраических уравнений относительно

, (5.2.7)

Раскрывая скалярные произведения, систему (5.2.7) можно переписать в виде

, (5.2.8)

Определитель матрицы системы (5.2.7)

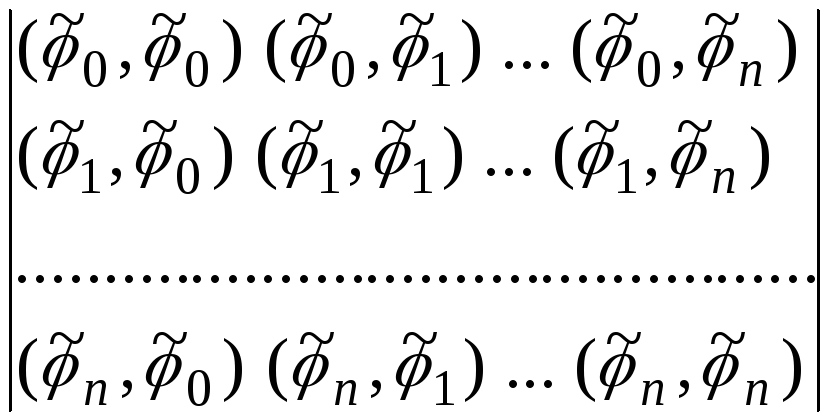(5.2.9)

получил название определителя Грамма. Если он отличен от нуля, то система (5.2.7) имеет единственное решение . Подставляя его в формулу (5.2.2), получим искомое приближение, которое является наилучшим в смысле меры близостии:

.

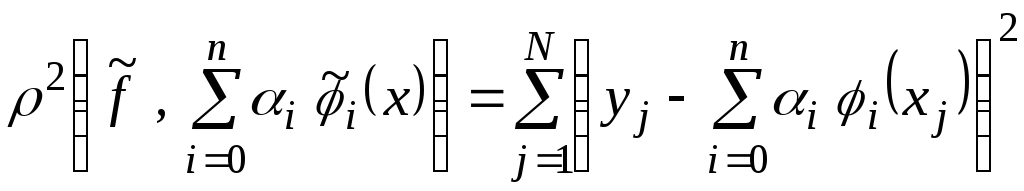Минимизируемая мера близости представляет собой сумму квадратов расстояний по вертикали между табличными точками и графиком функции .Поэтому описанный метод получения приближений называется методом наименьших квадратов. Приближение, получаемое методом наименьших квадратов, также называют среднеквадратическим.

Вопрос о существовании и единственности наилучшего среднеквадратического приближения, полученного по методу наименьших квадратов, в общем случае требует дополнительного исследования, поскольку достаточные условия минимума функции не проверялись и определитель Грамма, вообще говоря, может обращаться в ноль.