251

Глава 5. Наилучшее среднеквадратическое приближение

Глава 5. Наилучшее среднеквадратическое приближение

В предыдущей главе подробно рассмотрен один из самых распространенных способов приближения функций – интерполирование. Но этот способ не единственный. При решении разнообразных прикладных задач и построении вычислительных схем нередко используют и другие способы. В этой главе мы рассмотрим способы получения среднеквадратических приближений. Название приближений связано с метрическими пространствами, в которых рассматривается задача приближения функции. В главе 1 мы ввели понятия «метрическое линейное нормированное пространство» и «метрическое евклидово пространство» и увидели, что погрешность приближения определяется метрикой пространства, в котором рассматривается задача приближения. В разных пространствах понятие погрешности имеет разный смысл. Рассматривая погрешность интерполяции, мы не акцентировали на этом внимание. А в этой главе нам придется этим вопросом заняться более подробно.

5.1. Приближения тригонометрическими многочленами и многочленами Лежандра Пространство l2[a;b]

Рассмотрим множество функций , интегрируемых с квадратом по Лебегу на отрезке, то есть таких, что должен существовать интеграл.

Поскольку выполняется очевидное неравенство , из интегрируемости с квадратом функцийидолжна следовать и интегрируемость с квадратом любой их линейной комбинации, (гдеи любые вещественные числа), а также интегрируемость произведения .

Введем на множестве функций, интегрируемых с квадратом по Лебегу на отрезке , операцию скалярного произведения

. (5.1.1)

Из свойств интеграла следует, что введенная операция скалярного произведения обладает почти всеми свойствами скалярного произведения в евклидовом пространстве (см. параграф 1.10, с. 57):

1. ;

2. ;

3. ;

4. .

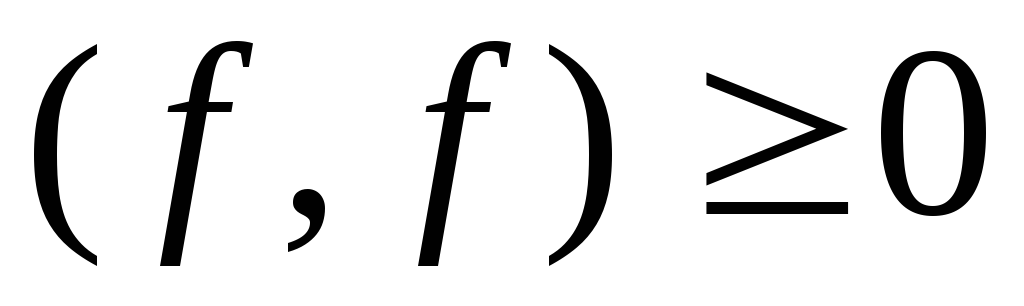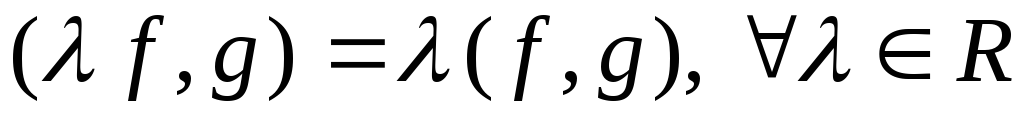Только первое свойство выполняется не до конца, то есть не будет выполнено условие.

В самом деле, если , то отсюда не следует, чтона отрезке. Для того чтобы введенная операция обладала этим свойством, в дальнейшем договоримся не различать (считать эквивалентными) функции и ,для которых

.

С учетом последнего замечания, мы убедились, что множество интегрируемых с квадратом по Лебегу функций (точнее множество классов эквивалентных функций) образует евклидово пространство, в котором определена операция скалярного произведения по формуле (5.1.1). Это пространство называют пространством Лебега и обозначают или короче.

Поскольку всякое евклидово пространство автоматически является и нормированным и метрическим, пространство также является нормированным, и метрическим пространством. Норма (величина элемента) и метрика (расстояние между элементами) в нем обычно вводятся стандартным способом:

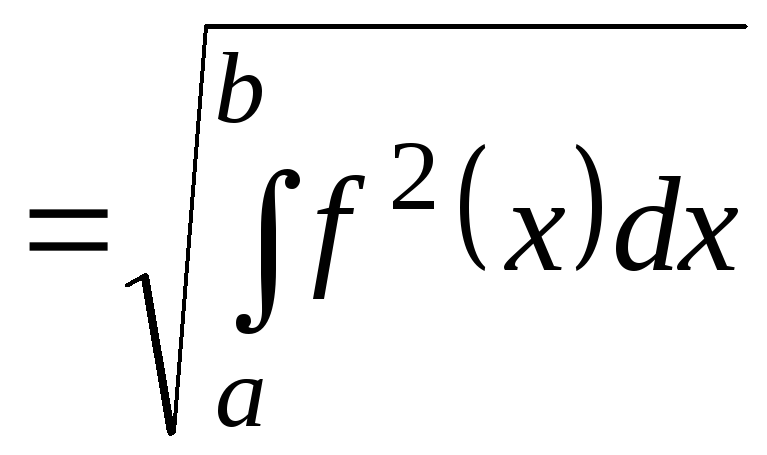(5.1.2)

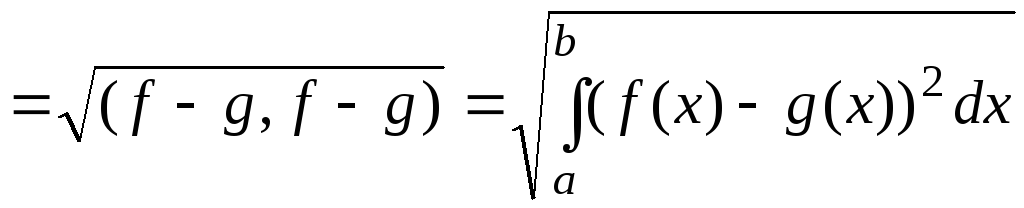(5.1.3)

Свойства (аксиомы) нормы и метрики приведены в параграфе 1.10. Элементами пространства являются не функции, а классы эквивалентных функций. Функции, принадлежащие одному классу, могут иметь разные значения на любом конечном или даже счетном подмножестве . Поэтому приближения в пространствеопределяются неоднозначно. Эта неприятная особенность пространстваокупается удобствами использования скалярного произведения.