Квадратурная формула Гаусса

Этот метод характеризуется высокой точностью при небольшом числе точек, используемых для расчетов.

Рассмотрим функцию на отрезке. Для вычисления интеграла по методу Гаусса на отрезке выбираютсяточек.

Квадратурная формула Гаусса записывается на основе полиномов Лежандра

. (6.5)

Запишем несколько первых полиномов:

Полиномы Лежандра обладают следующими свойствами:

1. 

2. , где 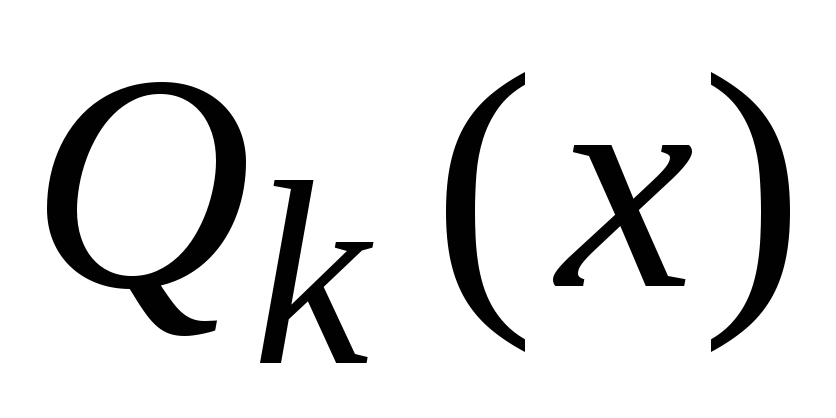- любой полином степени.

При вычислении интеграла по квадратурной формуле Гаусса (6.6)

необходимо найти значения коэффициентов и точки.

Точки находятся как нули соответствующего полинома Лежандра (степени)

,

которые могут быть найдены, например, методом поразрядного приближения с требуемой точностью .

Для определения коэффициентов используется система

Уравнения данной системы составляются следующим образом:

. (6.7)

Пример. Пусть требуется вывести квадратурную формулу Гаусса с использованием трех вспомогательных точек. Сначала находятся нули , то есть корни уравнения

Для этого уравнения корни всегда равны следующим значениям:

,.

Коэффициенты найдем из системы линейных алгебраических уравнений (6.7):

тогда .

Следовательно, для любой функции квадратурная формула Гаусса с тремя точками запишется следующим образом:

.

Для вычисления общего интеграла используется замена переменной. (6.8)

Получим

.

Применяя к последнему интегралу квадратурную формулу Гаусса, получим

, (6.9)

где ; нули полинома Лежандра .

Задание

1. Составить программу, реализующую вычисление интеграла любой заданной функции методом трапеций.

2. Составить программу, реализующую вычисление интеграла любой заданной функции методом прямоугольников.

3. Составить программу, реализующую вычисление интеграла любой заданной функции методом парабол.

4. Составить программу, реализующую вычисление интеграла любой заданной функции методом Гаусса. Использовать полином Лежандра 3-й степени.

Описание программы, входных и выходных параметров

На рис. 6.1 представлено окно программы, в которой реализованы четыре метода численного интегрирования. В данном примере вычислялось значение интеграла от функции методом парабол с шагом.

Входными данными являются:

• функция f(x), выбранная из 2 или 3 заданных;

• отрезок ;

• число шагов или шаг.

Выходные данные - значение интеграла.

Вычисления реализовывать в функции, параметрами которой являются входные данные и указатель на функцию, являющуюся подынтегральным выражением, возвращаемое значение  значение интеграла.

Рис. 6.1. Окно программы вычисления интегралов

Лабораторная работа 7 численное решение дифференциальных уравнений

Цель и задачи работы: изучение методов численного решения дифференциальных уравнений и получение навыков их практического использования.

Методы Рунге-Кутта

Дифференциальное уравнение первого порядка, разрешенное относительно производной, имеет вид

. (7.1)

Решением дифференциального уравнения (7.1) называется функция , подстановка которой в уравнение обращает его в тождество:. График решенияназываетсяинтегральной кривой. Например, решением уравнения является функцияпри любом значении произвольной постоянной С.

Задача Коши для дифференциального уравнения (7.1) состоит в том, чтобы найти решение уравнения (7.1), удовлетворяющее начальному условию

. (7.2)

Пару чисел называютначальными данными. Решение задачи Коши называется частным решением уравнения (7.1) при условии (7.2). Например, частным решением задачи Коши

,

является функция . Частному решению соответствует одна из интегральных кривых, проходящая через точку.

Численное решение задачи Коши (7.1), (7.2) состоит в том, чтобы получить искомое решение в виде таблицы его приближенных значений для заданных значений аргументана некотором отрезке. Точкиназываютузловыми точками, а множество этих точек - сеткой на отрезке . Будем использовать равномерную сетку с шагом:

; ; .

Приближенные значения численного решения задачи Коши в узловых точках обозначим через :. Для любого численного метода решения задачи Коши начальное условие (7.2) выполняется точно, т. е..

Величина погрешности численного метода решения задачи Коши на сетке отрезка оценивается величиной

, ,

т. е. расстоянием между векторами приближенного решения и точного решенияна отрезке поm-норме. Когда шаг стремится к нулю, погрешностьтакже стремится к нулю.

Численные методы решения задачи Коши на равномерной сетке отрезка с шагомявляются методами Рунге-Кутта, если, начиная с данных, решение ведется по следующим рекуррентным формулам:

(7.3)

Метод называют методом Рунге-Кутта порядка , если он имеет-й порядок точности по шагуна сетке. Порядок точностидостигается с помощью формул (7.3) при определенных значениях коэффициентови;всегда полагают равным нулю.

Методы Эйлера и Эйлера-Коши можно назвать, соответственно, методами Рунге-Кутта 1-го и 2-го порядков.

Графиком приближенного решения является ломаная, последовательно соединяющая точки . С увеличением порядка численного метода звенья ломаной приближаются к ломаной, образованной хордами интегральной кривой.

Практическая оценка погрешности решения, найденного на сетке с шагом , в точкепроизводится с помощьюправила Рунге:

, (7.4)

где  порядок точности численного метода.

Если требуется решить дифференциальное уравнение с некоторой заданной точностью , следует проводить вычисления с уменьшающимся вдвое шагом до достижения требуемой точности, т. е. до выполнения условия,. (7.5)