
- •Вычислительная математика
- •210100 "Управление и информатика в технических системах"
- •680035, Хабаровск, ул. Тихоокеанская, 136.
- •Прямые методы решения систем линейных алгебраических уравнений Метод Гаусса
- •Метод Гаусса с выбором главного элемента по столбцам
- •Итерационные методы решения систем линейных алгебраических уравнений
- •Нормы матриц
- •Итерационные методы решения систем линейных алгебраических уравнений Метод простых итераций
- •Метод Зейделя
- •Задания
- •Описание программы, входных и выходных параметров
- •Контрольные вопросы
- •Лабораторная работа 2 решение нелинейных уравнений
- •Решение алгебраических уравнений методом половинного деления
- •Метод отделения корней
- •Метод итераций
- •Метод поразрядного приближения
- •Задания
- •Описание программы, входных и выходных параметров
- •Контрольные вопросы
- •Точечное среднеквадратичное приближение функций многочленами Чебышева
- •Задания
- •Контрольные вопросы
- •Лабораторная работа 4 интерполирование функций
- •Интерполяционная формула Лагранжа
- •Интерполяция кубическими сплайнами
- •Задание
- •Контрольные вопросы
- •Лабораторная работа5
- •Описание программы, входных и выходных параметров
- •Контрольные вопросы
- •Лабораторная работа 6 Численное интегрирование
- •Квадратурные формулы интегрирования
- •Метод трапеций
- •Метод прямоугольников
- •Метод Симпсона (парабол)
- •Квадратурная формула Гаусса
- •Задание
- •Лабораторная работа 7 численное решение дифференциальных уравнений
- •Методы Рунге-Кутта
- •Метод Эйлера
- •Метод Эйлера-Коши
- •Метод Рунге-Кутта 4-го порядка
- •Задание
- •Контрольные вопросы
- •Лабораторная работа8 поиск экстремумов функции
- •Сужение промежутка унимодальности
- •Численные методы поиска минимума функции одной переменной Метод половинного деления
- •Метод золотого сечения
- •Метод сканирования
- •Задание
- •Контрольные вопросы
- •Библиографический список
- •Оглавление
Министерство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
"Хабаровский государственный технический университет"
Вычислительная математика
Методические указания по выполнению лабораторных работ 1 8
для студентов 2-го курса специальностей
210100 "Управление и информатика в технических системах"
и 071900 "Информационные сети"
Хабаровск
Издательство ХГТУ
2004
УДК
Вычислительная математика: Методические указания по выполнению лабораторных работ для студентов специальностей 210100 "Управление и информатика в технических системах" и 071900 "Информационные системы" / Сост. И. В. Епанешникова. Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2004. -42 с.
Методические указания разработаны на кафедре "Автоматика и системотехника" и предназначены для оказания помощи студентам, выполняющим лабораторные работы по дисциплине "Вычислительная математика".
Содержат сведения по основным численным методам, варианты заданий и краткое описание хода выполнения лабораторных работ.
Печатается в соответствии с решениями кафедры "Автоматика и системотехника" и методического совета ИИТ.
Главный редактор Л. А. Суевалова Редактор Л. С. Бакаева Компьютерная верстка И. В. Епанешниковой
Подписано в печать . Формат 60 x 84 1/16. Бумага писчая. Гарнитура “Таймс”. Печать офсетная. Усл. печ. л. . Тираж 150 экз. Заказ .
Издательство Хабаровского государственного технического университета.
680035, Хабаровск, ул. Тихоокеанская, 136.
Отдел оперативной полиграфии издательства
Хабаровского государственного технического университета.
680035, Хабаровск, ул. Тихоокеанская, 136.
Хабаровский государственный технический университет, 2004
Лабораторная работа 1
РЕШЕНИЕ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Цель и задачи работы: изучение прямых и итерационных методов решения систем линейных алгебраических уравнений.
К решению систем линейных алгебраических уравнений (СЛАУ) сводятся многие задачи (идентификация, оптимальное управление), они являются основой решения других задач вычислительной математики (системы дифференциальных уравнений и т. д.).
Методы решения СЛАУ разделяются на две группы:
Точные, или прямые, методы. Они характеризуются тем, что погрешность, как правило, определяется только погрешностью округления. К этой группе относятся методы Крамера, Гаусса и его модификации, прогонки и т. д. Метод Крамера менее эффективен для использования при решении задач на ЭВМ, поскольку требует большого числа арифметических операций. Метод Гаусса эффективен до порядка системы
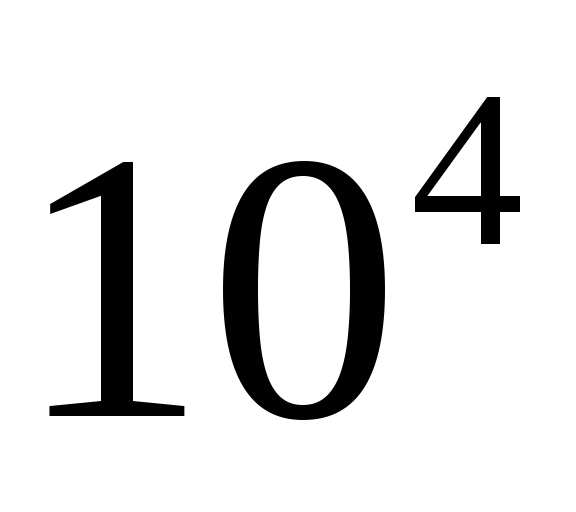 .
.Итерационные. Основаны на получении и уточнении последовательных приближений к точному решению. Эффективны, когда много нулевых коэффициентов и высок порядок системы. Методы: простых итераций, Зейделя и т. д. Эффективны до порядка систем
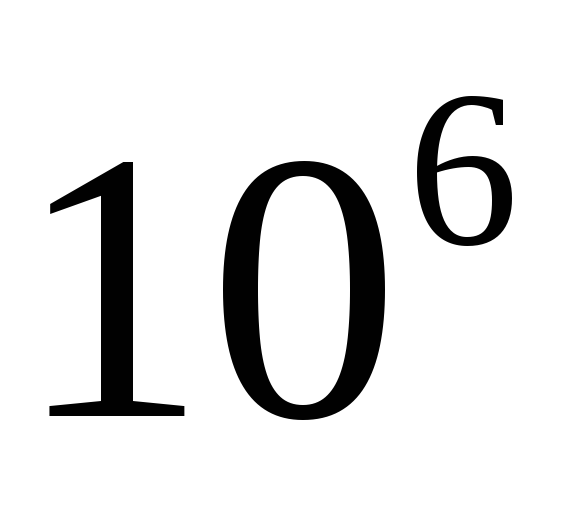 .
.
С помощью этих методов решаются системы вида
 (1.1)
(1.1)
или,
иначе, векторно-матричных уравнений
![]() ,
где
,
где![]() -
вещественная матрица коэффициентов
системы
-
вещественная матрица коэффициентов
системы![]() ;
;![]() - вектор свободных членов;
- вектор свободных членов;![]() -
вектор неизвестных.
-
вектор неизвестных.
Решение существует и является единственным, если выполняется условие
![]() .
.
Прямые методы решения систем линейных алгебраических уравнений Метод Гаусса
Метод
Гаусса заключается в последовательном
исключении неизвестных. Предположим,
что
![]() .
В противном случае можно поменять
местами первое уравнение с уравнением,
в котором коэффициент при
.
В противном случае можно поменять
местами первое уравнение с уравнением,
в котором коэффициент при![]() не равен 0.
не равен 0.
Разделим первое уравнение системы на
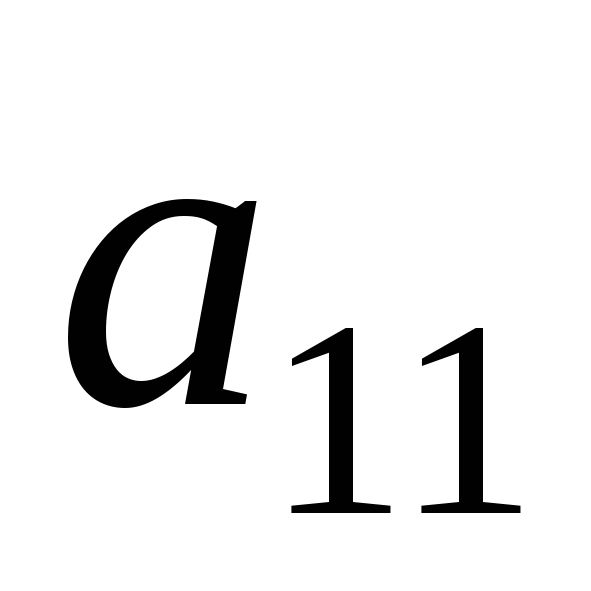 .
Получим
.
Получим
![]() ,
(1.2)
,
(1.2)
где
![]() ;
;![]() .
.
Умножим разрешающее уравнение (1.2) на
 и вычтем полученное уравнение из второго
уравнения системы (1.1). Аналогично
преобразуем остальные уравнения:
и вычтем полученное уравнение из второго
уравнения системы (1.1). Аналогично
преобразуем остальные уравнения:
 (1.3)
(1.3)
где
![]() ,
,![]() ,…
,
,…
,
![]() ,
,![]() (j=2,
3,…, n).
(j=2,
3,…, n).
Если
коэффициент
![]() ,
тоi-е
уравнение системы (1.1) войдет в систему
(1.3) без изменений, т. е.
,
тоi-е
уравнение системы (1.1) войдет в систему
(1.3) без изменений, т. е.
![]() ,
,![]() ,
(i
= 2, 3,…, n).
,
(i
= 2, 3,…, n).
Оставив без изменений первое уравнение, можно сделать второе уравнение разрешающим и применить описанную процедуру к системе из
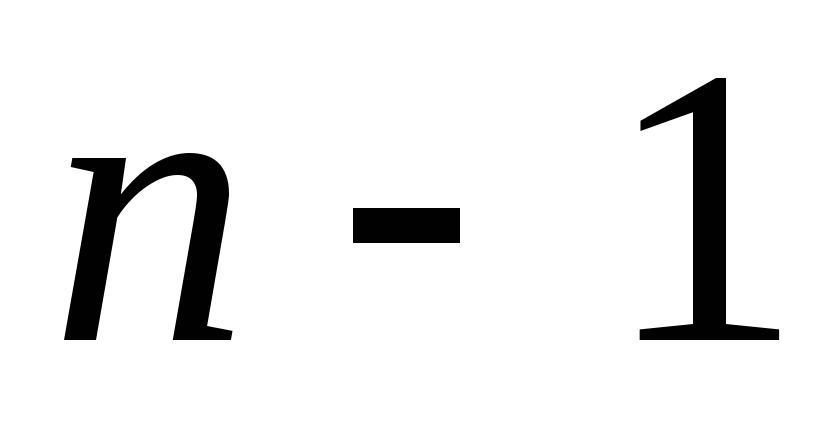 уравнений, исключив
уравнений, исключив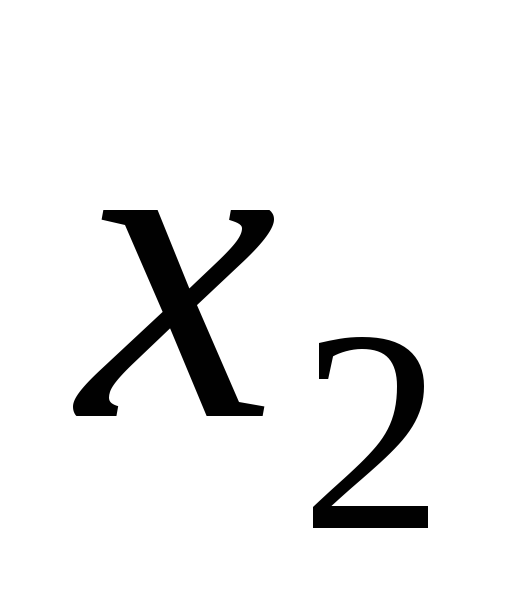 из третьего и последующих уравнений
из третьего и последующих уравнений
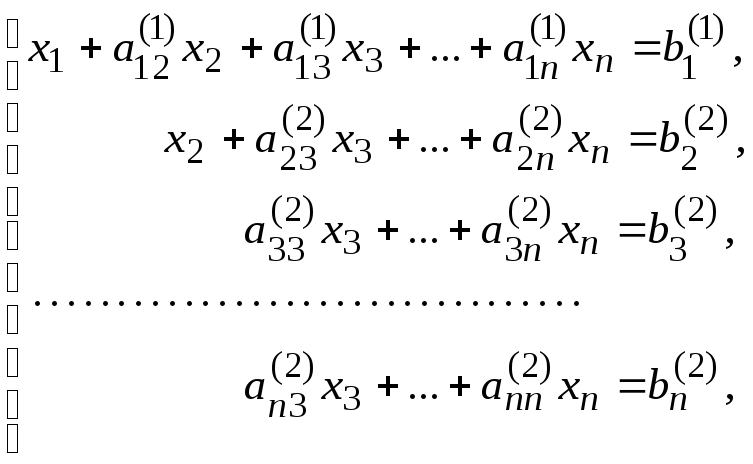
где
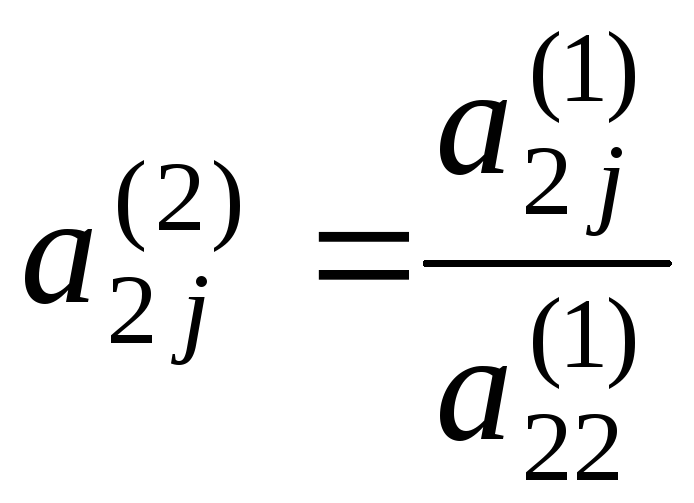 ,
,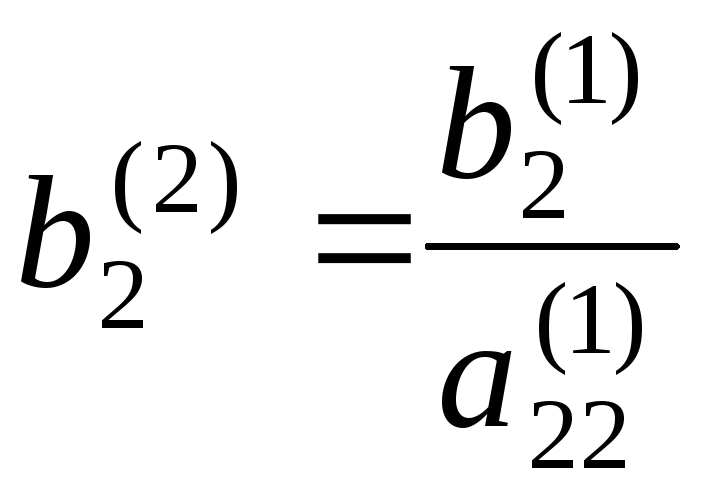 ,
,![]() ,…,
,…,![]() ,
,![]() (j=3,
4,…, n).
(j=3,
4,…, n).
Продолжая аналогичные вычисления, приведем систему (1.1) к эквивалентной системе
 (1.4)
(1.4)
Приведение системы (1.1) к эквивалентной системе (1.4) - прямой ход метода Гаусса. При обратном ходе происходит вычисление неизвестных, начиная с последнего, по формуле
 .
.
Алгоритм данного метода можно записать следующим образом.
Для
 ;
;для
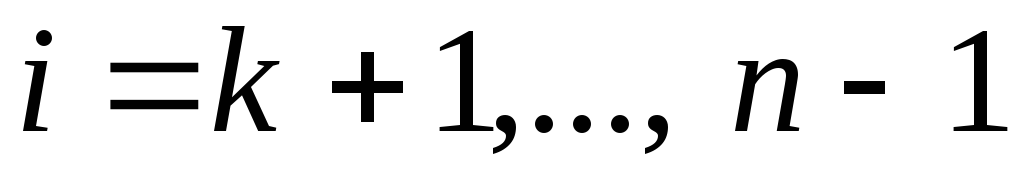 ;
;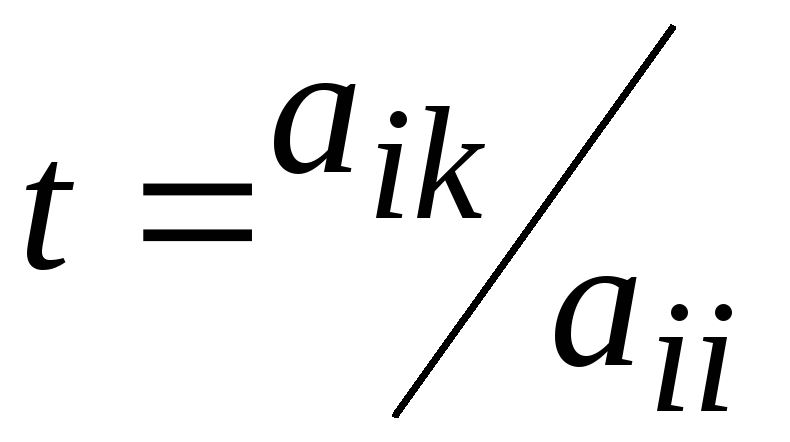 ;
;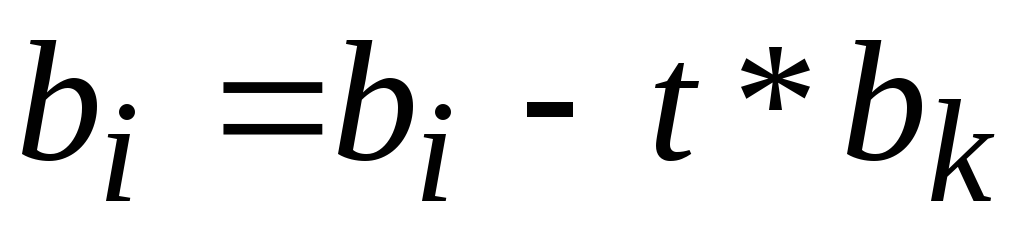 ;
;для
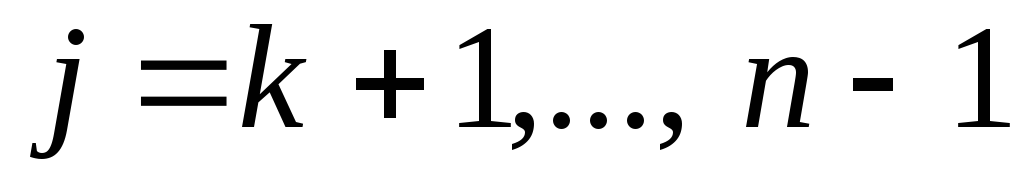 ;
; ;
;Для
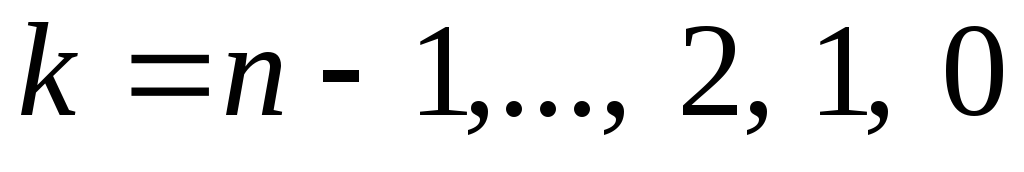 ;
;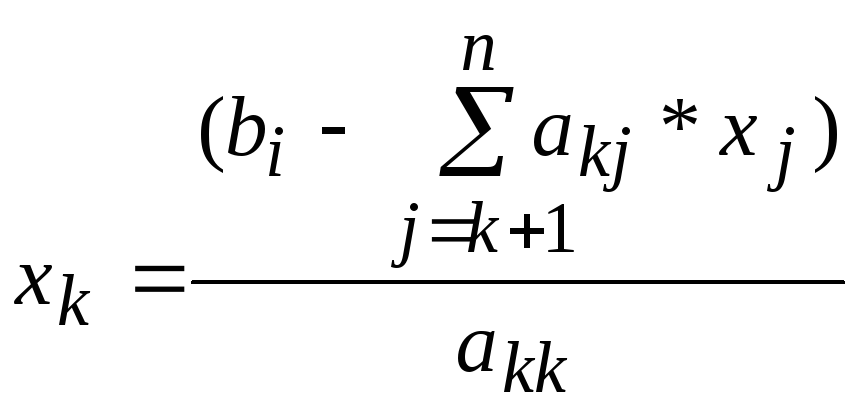 .
.
Здесь пункты 1 6 представляют собой прямой ход, пункты 7 и 8 обратный ход метода Гаусса.
