Точечное среднеквадратичное приближение функций многочленами Чебышева

Пусть на множестве точек задана функцияи определена система функций.

Скалярным произведением функций и на множестве точек называется сумма произведений значений этих функций, вычисленных во всех точках, т. е.

.

Число называетсянормой функции на множестве точек .

Коэффициенты обобщенного многочлена

называются коэффициентами Фурье функции относительно ортогональной системы функций, если определяются по формулам

.

Квадрат наименьшего среднеквадратичного отклонения определяется соотношением , где- коэффициенты Фурье.

Оценка погрешности приближения определяется величиной

.

Многочленами Чебышева на множестве точек называются многочлены ортогональные на этом множестве, с нормой, отличной от нуля, и определяемые следующими рекуррентными формулами:

; ;,

где

;;.

Задания

1. Написать программу для аппроксимации аналитически заданной функцией с помощью тригонометрических многочленов.

В данной программе следует предусмотреть возможность ввода степени многочлена n и величины отрезка l (визуальный компонент TEdit), вывода коэффициентов и(визуальный компонентTStringGrid) и построения графиков заданной функции и аппроксимирующего многочлена.

2. Написать программу для аппроксимации таблично заданной функции с помощью многочленов Чебышева.

В данной программе должны вводиться значения степени многочлена n, числа точек m, таблицы значений функции и. Результат работы программы – таблица параметров,и коэффициентов Фурье, а также график заданной функции и аппроксимирующего многочлена.

Нарис. 3.1 представлено окно программы, в которой реализован метод аппроксимации с помощью тригонометрических многочленов.

Рис.3.1. Аппроксимация тригонометрическими многочленами

Жирной линией изображен график исходной функции, тонкой линией  график аппроксимирующего многочлена .

Контрольные вопросы

1. Что такое аппроксимация?

2. В чем отличие между аппроксимацией аналитически и таблично заданных функций?

1. Какие функции называются ортогональными?

2. Чем характеризуется точность приближения?

Лабораторная работа 4 интерполирование функций

Цель и задачи работы: изучение методов интерполяции и получение навыков их применения при решении задач с помощью ЭВМ.

Интерполяционная формула Лагранжа

Пусть функция определена таблицей

			…
A			…

Значения аргументов называютсяузлами интерполяции.

Задачей интерполяции является построение многочлена , значения которого в узлах интерполяцииравны соответствующим значениям заданной функции, т. е.

.

Интерполяционной формулой Лагранжа называется формула, представляющая многочлен в виде

, (4.1)

где - многочлен степени, принимающий значение, равное 1, в узлеи 0 в остальных узлахи имеющий вид

. (4.2)

Многочлен (4.1) называется интерполяционным многочленом Лагранжа. Степень многочлена Лагранжа не превышает .

Интерполяция кубическими сплайнами

Пусть отрезок разбит начастей точками:

.

Сплайном k-й степени называется функция, представляющая собой многочлен не выше k-й степени на каждом из последовательно примыкающих друг к другу интервалов . Функция непрерывна вместе со своими производными до порядка не вышеk.

Например, непрерывная кусочно-линейная функция (ломаная) является сплайном первой степени с производной, терпящей разрыв в точках излома.

Пусть на отрезке определена функция, значения которой в точкахравны.

Задача интерполяции функции на отрезке кубическим сплайном(сплайном третьей степени)состоит в нахождении функции, равной многочлену третьей степенина каждом отрезке ,т. е.

, , (4.3)

причем значения сплайна в узлах интерполяции равны соответствующим значениям заданной функциии сплайн-функция непрерывна в узлах интерполяции вместе с производными первого и второго порядков:

, (4.4)

, (4.5)

, (4.6)

. (4.7)

Условия (4.4)  (4.7) дают линейных алгебраических уравнений для определениянеизвестных коэффициентов(p=0, 1, 2, 3; i=1, 2,..., n) при соответствующих степенях в многочленах.

Интерполяционный кубический сплайн для функции существует и является единственным, если вместе с этими уравнениями выполняется какая-либо пара дополнительных (краевых) условий:

1. ;

2. ;

3. .

Рассмотрим случай разбиения отрезка наn равных частей с шагом h, для которого ис использованием краевых условий 1-го типа.

Введем величины (наклоны сплайна в точках(i=0, 1,..., n)).

Интерполяционный кубический сплайн вида

(4.8)

удовлетворяет условиям (4.4) ‑ (4.6) для любых . Из условия (4.7) и краевых условий 1-го типа можно определитьn+1 параметр :

.

Учитывая, что

а также краевые условия 1-го типа и условия (4.7), то получим систему из n+1 линейных уравнений относительно неизвестных :

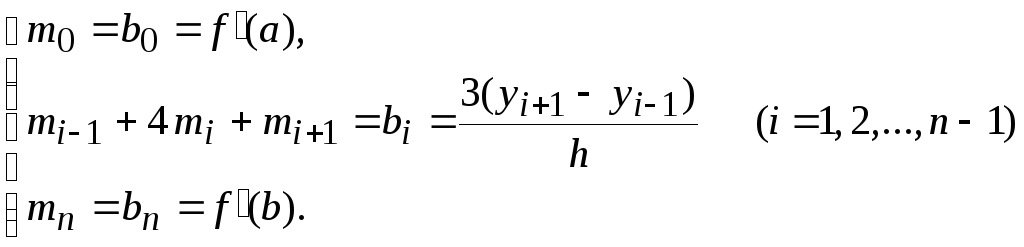(4.9)

Решение этой системы позволяет найти значения неизвестных и определить интерполяционный сплайн в виде соотношений (4.8). Система (4.9) может быть решена методом Гаусса или одной из его модификаций.