Численные методы поиска минимума функции одной переменной Метод половинного деления

Пусть определен отрезок , которому принадлежит точка локального минимума, и функцияявляется унимодальной на этом отрезке.

Используем точки, расположенные симметрично относительно середины отрезка :, где. Тогда точкиипринадлежат отрезку, и, следуя рассмотренной выше схеме сужения промежутков унимодальности, получим новый суженный отрезоки оценим его длину в каждом из трех возможных случаев:

1. .

2. .

3. .

Таким образом, после первого шага преобразований найден новый отрезок унимодальности, длина которого уменьшилась. Название метода (половинного деления) мотивировано тем, что если величина очень мала, то отрезок уменьшается почти вдвое (в случаях 1 и 2).

Вычисления продолжаются до тех пор, пока не будет достигнута требуемая точность .

Метод золотого сечения

Точка являетсязолотым сечением отрезка , если отношение длинывсего отрезка к длинебольшей части равно отношению большей части к длине меньшей части, т. е.. Аналогично, точка, симметричная точкеотносительно середины отрезка, является вторым золотым сечением этого отрезка.

Так как точки исимметричны относительно середины отрезка, то можно записать

, (8.1)

где . Свойство золотого сечения: точкаодновременно является золотым сечением отрезка, а другая точка золотым сечением отрезка .

При поиске минимума функции используется следующий алгоритм:

1. На исходном отрезке по формуле (8.1) принайдем точкии, а затем разность.

2. Вычисляются значения функции и, и по схеме сужения промежутка унимодальности образуется суженный отрезок.

3. На полученном отрезке находятся два сеченияи. При этом возможны три случая:

1. .

2. .

3. .

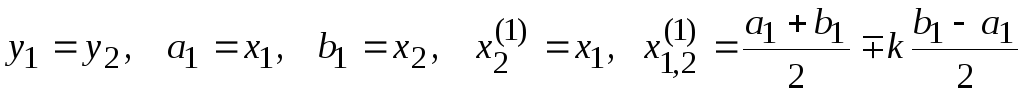4. По приведенной схеме находятся отрезки ,и т. д., с учетом того, что в случаях 1) и 2) значениеилицелевой функции уже получено на предыдущем шаге.

5. Точность приближенного равенства на-м шаге вычислений можно оценить неравенством,

где .

Метод сканирования

Пусть функция является унимодальной на некотором промежутке. Предположим, что произвольная точкаэтого промежутка является исходной для поиска точки локального минимума и число- заданная точность нахождения. Обозначим черезпроизвольное приращение аргументаи, сделав один шаг от точки, получим новое значение аргумента.

Сравним возможные значения функции и. Возможны три варианта продолжения приближения к точке минимума.

1. произошло уменьшение значения функции. В качестве нового стартового значения принимается . Вычисления по этой схеме продолжаются до тех пор, пока не произойдет увеличение значения функции, т. е., и если при этом, то принимаемс погрешностью. В противном случае полагаем, что точкаявляется исходной для продолжения вычислений по следующей схеме 2.

2. значение функции возросло. В этом случае полагаем, что начальной точкой вычислений является точка , а меньшим шагом для продолжения вычислений – величина, где- некоторое целое число,. Далее производим вычисления по схеме 1 или 2 до достижения требуемой точности.

3. (маловероятно). Принимается либо при достижении требуемой точности, либо следовать схеме 2.

Поиск минимума функции одной переменной данным методом представляет собой колебательный процесс около точки локального минимума функции с непрерывно уменьшающейся амплитудой.

Для определения точки локального минимума метод сканирования применим без предварительного нахождения промежутков унимодальности функции. С помощью метода сканирования можно найти различные точки локального минимума, если целевая функция имеет не один минимум.