Метод Эйлера

Метод Эйлера является самым простым и неточным из рассматриваемых в данной лабораторной работе. Метод Эйлера иногда называют методом Рунге-Кутта 1-го порядка.

Алгоритм метода Эйлера можно получить из формул (7.3):

; отсюда

. (7.6)

Метод Эйлера-Коши

Формулы метода Эйлера-Коши получаются из соотношений (7.3) при ,,,:

(7.7)

Метод Рунге-Кутта 4-го порядка

Метод Рунге-Кутта четвертого порядка называют классическим методом Рунге-Кутта, если ,,,,,. Из рекуррентных формул (7.3) получим алгоритм решения задачи Коши классическим методом Рунге-Кутта:

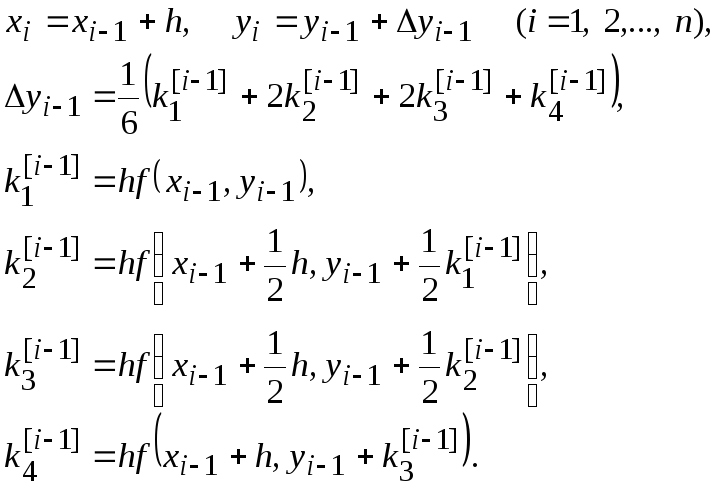(7.8)

Задание

Написать программу решения дифференциального уравнения первого порядка на равномерной сетке отрезка , используя метод согласно варианту. Предусмотреть возможность ввода произвольных значений числа шагов, начальных условий и точности (варианты 4 6). Результаты вычислений представить в виде таблиц и графиков.

1. Метод Эйлера (метод Рунге-Кутта 1-го порядка).

2. Метод Эйлера-Коши (метод Рунге-Кутта 2-го порядка).

3. Метод Рунге-Кутта 4-го порядка.

4. Метод Эйлера с достижением заданной точности.

5. Метод Эйлера-Коши с достижением заданной точности.

6. Метод Рунге-Кутта 4-го порядка с достижением заданной точности.

Описание программы, входных и выходных параметров

Исходными данными являются:

• начальные условия ;

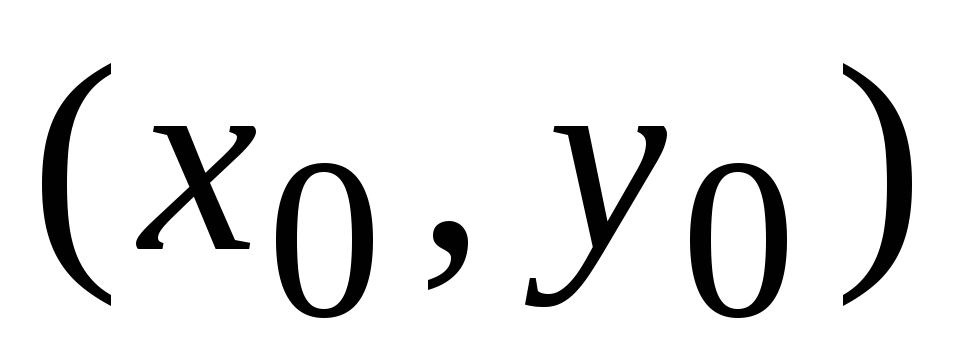• значение шага ;

• число шагов ;

• точность (для вариантов 4 6);

• функция , являющаяся правой частью дифференциального уравнения.

Результат:

• график  решения дифференциального уравнения;

• таблица значений.

Указанный в варианте метод должен реализовываться в функции, в которую должны передаваться исходные данные, необходимые для данного варианта. Возвращаемое значение  указатель на созданный в функции массив .

Нарис. 7.1 представлено окно программы, в которой проводилось решение выбранного дифференциального уравнения одним из трех методов.

Рис. 7.1. Решение дифференциальных уравнений

Контрольные вопросы

1. Как формулируется задача Коши?

2. На чем основаны одношаговые методы решения задачи Коши?

3. От чего зависит точность метода?

4. Какой из рассмотренных методов самый точный?

5. Какой из трех методов самый неточный?

6. Как можно оценить погрешность решения, найденного с шагом ?

7. Каким образом следует проводить вычисления, если требуется решить дифференциальное уравнение с заданной точностью ? Выполнение какого условия свидетельствует о том, что точность достигнута?

Лабораторная работа8 поиск экстремумов функции

Цель и задачи работы: изучение методов поиска экстремумов функций и получение навыков их практического использования.

Задача отыскания всех локальных минимумов (максимумов) функции называется задачей безусловной оптимизации, а функция- целевой функцией.

Сужение промежутка унимодальности

Пусть требуется решить задачу ,.

Применение численных методов для отыскания точек локального минимума функции предполагает:

1. определение промежутков унимодальности функции, то есть нахождение отрезков, которым принадлежит одна точка локального минимума;

2. вычисление значения , принадлежащего выбранному промежутку, с заданной точностью.

При вычислении точки минимума точность достигается последовательным уменьшением отрезка, содержащего точку ,до размеров, не превышающих заданную точность().

Пусть функция унимодальна на отрезке. Выбираются две произвольные точки, принадлежащие отрезку, такие, что. В каждом из следующих трех случаев можно указать отрезок меньших размеров, содержащий точку и принадлежащий первоначальному отрезку.

1. Если , то.

2. Если , то.

3. Если , то.

Методы вычисления значения точки минимума функции одной переменной отличаются алгоритмами выбора точек идля локализации точки с заданной точностью.