
- •Методические указания
- •Программа 1‑й части курса
- •Раздел I «Элементы теории вероятностей и математической статистики»
- •Введение
- •1.2 Непосредственный подсчёт вероятностей
- •1.3 Относительная частота. Теорема бернулли
- •1.4 Сумма событий. Теорема сложения вероятностей для несовместных событий
- •1.5 Произведение событий. Теорема умножения
- •1.6 Теорема сложения для совместных событий
- •1.7 Многократные испытания. Формула бернулли
- •2 Случайные величины и законы распределения их вероятностей
- •2.1 Виды случайных величин
- •2.2 Формы задания закона распределения дискретных случайных величин
- •2.3 Формы задания закона распределения для непрерывных случайных величин
- •2.4 Вероятность попадания случайной величины на заданный интервал
- •2.5 Числовые характеристики случайной величины. Математическое ожидание
- •2.6 Моменты. Дисперсия. Среднее квадратическое отклонение
- •3 Нормальный закон распределения
- •3.1 Нормальный закон и его основные параметры
- •3.2 Понятие о центральной предельной теореме
- •3.3 Вероятность попадания нормально распределённой случайной величины на заданный интервал
- •3.4 Интеграл вероятностей
- •3.5 Дополнительные характеристики разброса случайной величины
- •4 Элементы математической статистики
- •4.1 Основные задачи. Понятия
- •4.2 Числовые характеристики
- •4.3 Дополнительные характеристики: асимметрия и эксцесс
- •4.4 Определение закона распределения на основе опытных данных
- •4.5 Критерий согласия пирсона
- •4.6 Оценивание параметров
- •4.7 Доверительные интервалы и доверительная вероятность
- •5 Элементы корреляционного анализа
- •5.1 Понятие о статистических связях
- •5.2 Коэффициент корреляции
- •5.3 Уравнение регрессии
- •3. Составим уравнение регрессии на d:
4 Элементы математической статистики
4.1 Основные задачи. Понятия
463Equation Section (Next)Математическая статистика — наука, которая занимается разработкой методов приближённого решения вероятностных задач на основе статистических данных.
Основные задачи математической статистики:
Определение закона распределения случайной величины — задача сглаживания или выравнивания статистического ряда;
"Задача проверки правдоподобия гипотез", тесно связанная с первой задачей, позволяет ответить на вопрос: согласуются ли результаты опыта с гипотезой о подобранном законе распределения вида
 (для ответа на этот вопрос служат
"критерии согласия");
(для ответа на этот вопрос служат
"критерии согласия");Задача об определении наилучших оценок неизвестных параметров, например, параметров
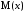 и
и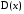 и задача оценки точности этих оценок.
и задача оценки точности этих оценок.
Основные понятия.
Результаты
наблюдений 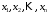 над случайной величинойХ
называют выборкой
из генеральной совокупности
(из всех
возможных
значений случайной величины Х).
над случайной величинойХ
называют выборкой
из генеральной совокупности
(из всех
возможных
значений случайной величины Х).
При
большом числе наблюдений выборку
оформляют в виде статистического
группированного ряда:
при этом весь диапазон значений хi
делится на интервалы, подсчитывается
количество значений xi,
приходящееся на каждый интервал mi
, затем
вычисляют частоты
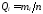 .
Составляют таблицу: статистический ряд
распределения.
.
Составляют таблицу: статистический ряд
распределения.
|
Таблица 4.1 | ||||
|
Интервалы |
|
|
… |
|
|
M |
m1 |
m2 |
… |
mi |
|
Q |
Q1 |
Q2. |
… |
Qi |
Практика показывает, что число интервалов k должно быть порядка 10–20.
Статистический ряд графически оформляется в виде гистограммы.
Для
этого по оси абсцисс откладывают
интервалы, на которых строят прямоугольники,
площади которых равны Qi (рис. 4.1).
Ясно, что
 .
Высоты прямоугольников вычисляют по
формуле
.
Высоты прямоугольников вычисляют по
формуле
|
|
47347\* MERGEFORMAT (.) |
Аналогом
функции распределения 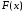 в математической статистике служит
статистическая функция распределения
в математической статистике служит
статистическая функция распределения
|
|
48348\* MERGEFORMAT (.) |
4.2 Числовые характеристики
Статистические начальные и центральные моменты определяются по формулам:
|
|
49349\* MERGEFORMAT (.) |
|
|
50350\* MERGEFORMAT (.) |
Статистические математическое ожидание, дисперсию и среднее квадратическое отклонение определяют соответственно по формулам:
|
|
51351\* MERGEFORMAT (.) |
|
|
52352\* MERGEFORMAT (.) |
|
|
53353\* MERGEFORMAT (.) |
4.3 Дополнительные характеристики: асимметрия и эксцесс
Нормированный центральный момент третьего порядка называют асимметрией (скошенностью)
|
|
54354\* MERGEFORMAT (.) |
а величина
|
|
55355\* MERGEFORMAT (.) |
называется
эксцессом
и является
мерой крутости, т.е. островершинности
или плосковершинности кривой. Для
кривой плотности нормального закона:
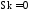 ,
,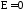 .
.
Критериями нормального закона служат неравенства [1,стр.84]:
|
|
56356\* MERGEFORMAT (.) |
где
|
|
57357\* MERGEFORMAT (.) |
Значительное
отклонение
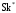 и
и от нуля, т.е. невыполнение условий 356,
означает отклонение исследуемого
распределения случайной величины от
нормального.
от нуля, т.е. невыполнение условий 356,
означает отклонение исследуемого
распределения случайной величины от
нормального.
4.4 Определение закона распределения на основе опытных данных
Исследование распределения статистического ряда начинается с построения гистограммы (рис. 4.1). По виду гистограммы, а также из соображений, связанных с существом задачи, делают предположение о виде теоретической кривой распределения. Если, например, исследуется ряд случайных ошибок измерений, то можно считать, что теоретической кривой является кривая нормального распределения вида 133.
Оценки 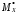 и
и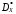 неизвестных параметров
неизвестных параметров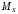 и
и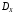 определяются по формулам 351 и 352.
Тогда уравнение кривой 133 принимает
вид
определяются по формулам 351 и 352.
Тогда уравнение кривой 133 принимает
вид
|
|
58358\* MERGEFORMAT (.) |
Выражение 358 обычно приводят к виду
|
|
59359\* MERGEFORMAT (.) |
где
|
|
60360\* MERGEFORMAT (.) |
выбирают из таблиц Приложения A по аргументу
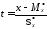 .
.
Затем
на графике гистограммы строится
выравнивающая её теоретическая кривая
по значениям хi и  ,
вычисленным для левых границ интерваловхi
(см. таблицу 4.1).
,
вычисленным для левых границ интерваловхi
(см. таблицу 4.1).
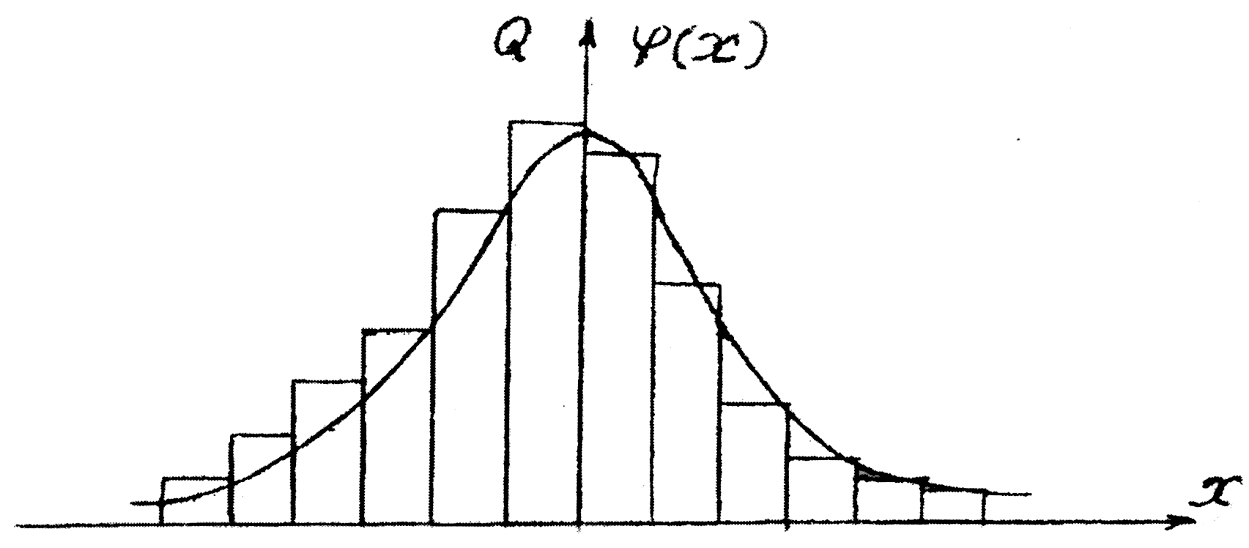
Рис. 4.1 —
Гистограмма и выравнивающая кривая 

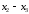
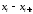
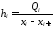 .
.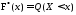 .
.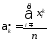 ;
;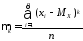 .
.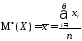 ;
;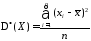 ;
;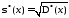 .
.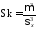 ,
,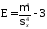
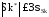 и
и
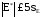 ,
,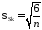 и
и
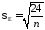 ,
,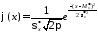 .
.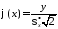 .
.