5.2 Коэффициент корреляции

Теснота линейной корреляционной связи между двумя величинами Х и Y (степень близости корреляционной связи к функциональной) характеризуется коэффициентом корреляции

,	66466\* MERGEFORMAT (.)

оценка которого определяется по формуле

,	67467\* MERGEFORMAT (.)

где 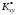— статистический корреляционный момент (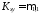— центральный смешанный момент второго порядка, важная числовая характеристика системы двух случайных величин).

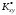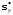, ,вычисляются по формулам:

; ;.	68468\* MERGEFORMAT (.)

Коэффициент корреляции изменяется в пределах .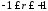

В случае, когда , имеет место отрицательная корреляция; при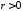говорят о положительной корреляции. Если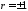, то имеет место функциональная прямолинейная связь; если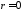, то междуХ и Y прямолинейная корреляционная связь отсутствует (однако другой вид связи может существовать).

Для оценки надёжности коэффициента корреляции при большом числе измерений () применяюткритерий Романовского: связь считается установленной, если выполняется условие

,	69469\* MERGEFORMAT (.)

где

.	70470\* MERGEFORMAT (.)

Для оценки надёжности 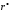при малом числе измерений () применяюткритерий Фишера (см. задачу 5.1).

5.3 Уравнение регрессии

Уравнение линейной регрессии Y на Х, отражающее прямолинейную корреляционную связь между переменными Х и Y, имеет вид:

,	71471\* MERGEFORMAT (.)

где 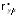— коэффициент регрессии Y на Х, вычисляемый по формуле

.	72472\* MERGEFORMAT (.)

Задача 5.1. В таблице 5.1 приведены результаты измерений линий D_i (в км) и абсолютные значения ошибок _i (в см).

Вычислить коэффициент корреляции; с вероятностью 0,90 оценить его надёжность и составить уравнение регрессии  на D.

Прежде чем решать задачу, прибегают к графическому изображению точек .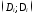

Рис. 5.1 — Прямая регрессии

График на рис. 5.1 указывает на наличие корреляции между D и .

Решение. Вычисление необходимых сумм, а также контроли вычислений поместим в таблице 5.1.

Таблица 5.1
№ п/п	, км	, см						Примечания
1	8,7	6,8	+4,0	+3,0	16,00	9,00	+12,00	1) ; ; . ; ;. ; . Контроль: . Контроль выполнен.
2	3,7	3,1	–1,0	–0,7	01,00	0,49	0+0,70
3	6,0	3,8	+1,3	–0,0	01,69	0,00	0+0,00
4	3,3	2,9	–1,4	–0,9	01,96	0,81	0+1,26
5	5,1	4,1	+0,4	+0,3	00,16	0,09	0+0,12
6	6,1	3,7	+1,4	–0,1	01,96	0,01	0–0,14
7	2,7	2,6	–2,0	–1,2	04,00	1,44	0+2,40
8	4,9	4,4	+0,2	+0,6	00,04	0,36	0+0,12
9	3,1	2,0	–1,6	–1,8	02,56	3,24	0+2,88
10	3,7	4,5	–1,0	+0,7	01,00	0,49	0–0,70
	47,3	37,9	+0,3	-0,1	30,37	15,93	+18,64

1. Вычисление 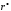по формуле 467, которая в данной задаче примет вид:

;

; ;.

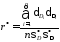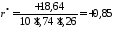2. Оценка надёжности 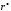. Так как число измерений сравнительно небольшое (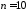), для оценки надёжности вычисленного значения коэффициента корреляции применимкритерий Фишера, основанный на преобразовании вида:

.	73473\* MERGEFORMAT (.)

По таблице Приложения C, пользуясь коэффициентом корреляции 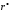, как аргументом, находим. Величинаподчинена нормальному закону распределения. Доверительный интервал для истинного значенияZ имеет вид:

.	74474\* MERGEFORMAT (.)

определяем по формуле

.	75475\* MERGEFORMAT (.)

Для вероятности 0,90 по таблице Приложения B находим .

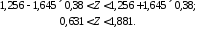
Из таблицы Приложения C находим соответствующие крайним значениям Z 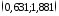значения границ коэффициента корреляции (0,56 и 0,95). Получаем доверительный интервал, с вероятностью 0,90 накрывающий истинное значениеr:

.

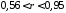Так как имеет место соотношение

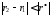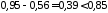(), то прямолинейную корреляционную связь можно считать установленной.
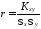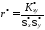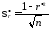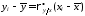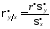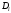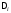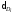
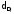
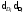
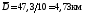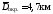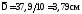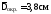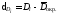
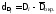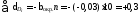
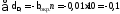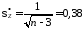