Теория одиночного снимка

1. Системы координат снимка. Элементы внутреннего ориентирования снимка.

Различают системы координат снимка в зависимости от типа камеры, с помощью которой получен снимок. На рис. 1.1.1 показаны системы координат для двух наиболее распространенных типов кадровых камер: аналоговый АФА (рис. 1.1.1а) и цифровая камера (рис. 1.1.1b).

Рис. 1.1.1

На каждом снимке имеются изображения координатных меток, которые определяют правую прямоугольную систему координат снимка o’xyz.

Ось х этой системы проходит через координатные метки 1-2 и направлена приблизительно по направлению полета. Началом системы координат является точка о’, получаемая в результате пересечения оси х с линией проведенной через координатные метки 3 и 4. Ось y лежит в плоскости снимка Р и перпендикулярна оси х. Ось z дополняет систему до правой.

На снимках, полученных с помощью цифровой камеры, координатные метки отсутствуют, а система координат снимка задается следующим образом. Начало системы координат о’ совпадает с пикселем, расположенным в левом нижнем углу матрицы изображения, ось x совпадает с соответствующей строкой, а ось y – с соответствующим столбцом этой матрицы (рис.1.1.1b). Ось z дополняет систему до правой.

В дальнейшем мы не будем акцентировать внимание на том, с помощью какого типа камеры были получены снимки. Так как последующая фотограмметрическая обработка снимков одинакова и не зависит от типа камеры (за исключением одного процесса - внутреннего ориентирования, который будет рассмотрен позже.

Любая точка снимка, например m, имеет в этой системе координат координаты m(х,у,z =0). Центр проекции S имеет в этой системе координаты S ( x=x_0, y=y_0, z=f ).

f - фокусное расстояние снимка, а х₀ и у₀ – координаты главной точки снимка - О.

Для восстановления связки проектирующих лучей, сформировавших снимок в системе координат снимка o’xyz, необходимо для каждой точки снимка определить координаты вектора в этой системе координат по измеренным на снимке координатам точки m.

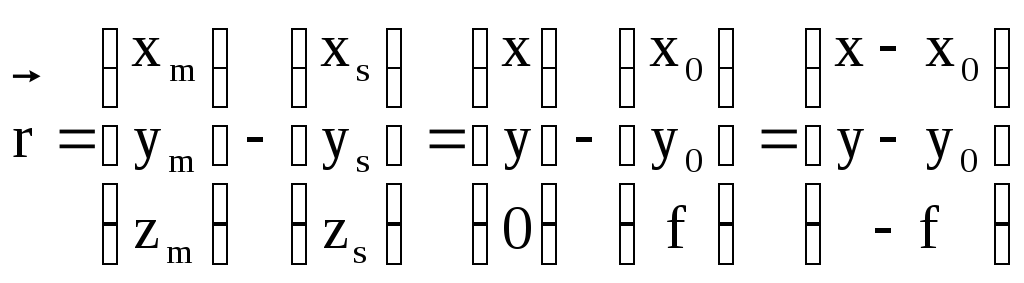. (1.1.1)

Из выражения (1.1.1) следует, что для восстановления связки проектирующих лучей, необходимо измерить координаты точки и знать значения координат центра проекции S в системе координат снимка f , х₀ , y₀, которые являются постоянными для данного снимка и называются элементами внутреннего ориентирования снимка.

Более широко в фотограмметрии используют систему координат снимка Sxyz , началом которой является центр проекции S, а оси координат параллельны соответствующим осям системы координат o’xyz.

Так как система координат Sxyz параллельна системе координат o’xyz, то, как известно из аналитической геометрии, координаты векторов в обеих системах координат равны, то есть координаты вектора в системе координат Sxyz определяется выражением (1.1.1).

2. Системы координат объекта. Элементы внешнего ориентирования снимка.

Положение точек объекта (местности) по снимкам определяют в прямоугольной пространственной системе координат OXYZ . В зависимости от решаемой задачи в качестве этой системы координат используют:

• государственную картографическую систему координат (в России – Гаусса – Крюгера);

• геоцентрическую систему координат;

• произвольную систему координат, связанную с характерными точками объекта (местности).

Положение и ориентацию системы координат снимка (или, что то же самое – снимка) в системе координат объекта OXYZ определяют элементы внешнего ориентирования снимка .

Положение центра проекции S в системе координат объекта определяют его координаты Xs,Ys,Zs.

Угловая ориентация системы координат снимка относительно системы координат объекта определяется ортогональной матрицей:

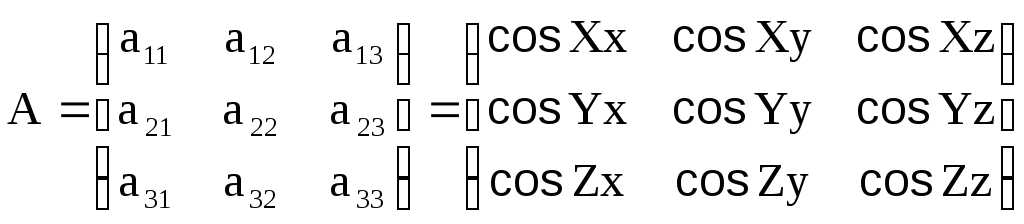(1.2.1)

В матрице А элементы (направляющие косинусы) а_ij являются косинусами пространственных углов между осями координат системы координат объекта OXYZ и снимка Sxyz.

Направляющие косинусы являются координатами единичных векторов (ортов), совпадающих с осями координат снимка в системе координат объекта.

Вследствие особых характеристик ортогональной матрицы:

А^-1=А^т;

а АА^т = Е = .

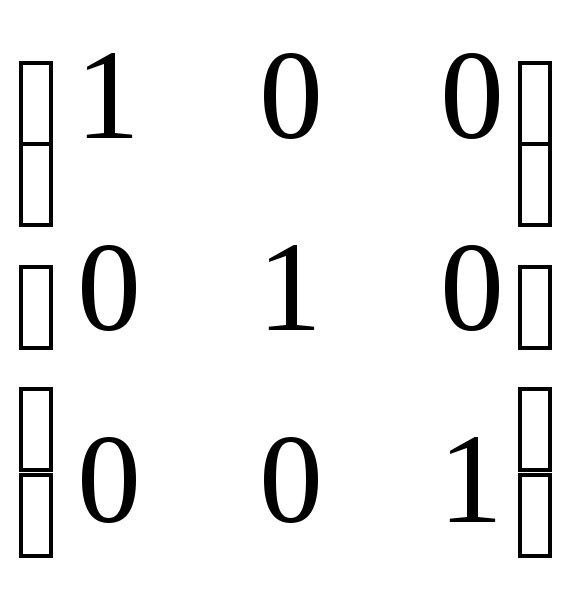В ортогональной матрице независимы только 3 элемента, следовательно элементы матрицы являются функцией 3 параметров.

В качестве этих параметров в фотограмметрии используют 3 угла - ,  и , которые называют угловыми элементами внешнего ориентирования снимка.

Последовательно поворачивая систему координат объекта OXYZ на эти углы вокруг ее осей, можно ориентировать ее параллельно осям системы координат снимка. При этом последовательность и направление поворотов могут быть произвольными. Поэтому в фотограмметрии используют различные системы угловых элементов ориентирования снимка.

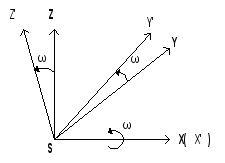
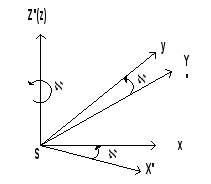
Рассмотрим наиболее широко используемую систему, в которой система координат объекта OXYZ поворачивается последовательно против часовой стрелки (правые углы) вокруг осей X,Y и Z соответственно на углы ,  и .

Геометрическая интерпретация угловых элементов внешнего ориентирования показана на рис.1.2.1.

 - поперечный угол наклона. Угол в координатной плоскости YZ между осью Z и проекцией оси z на плоскость YZ;

 - продольный угол наклона. Угол между проекцией оси z на плоскость YZ и осью z;

 - угол разворота снимка. Угол в плоскости снимка Р между следом сечения этой плоскости плоскостью Xz и осью х снимка.

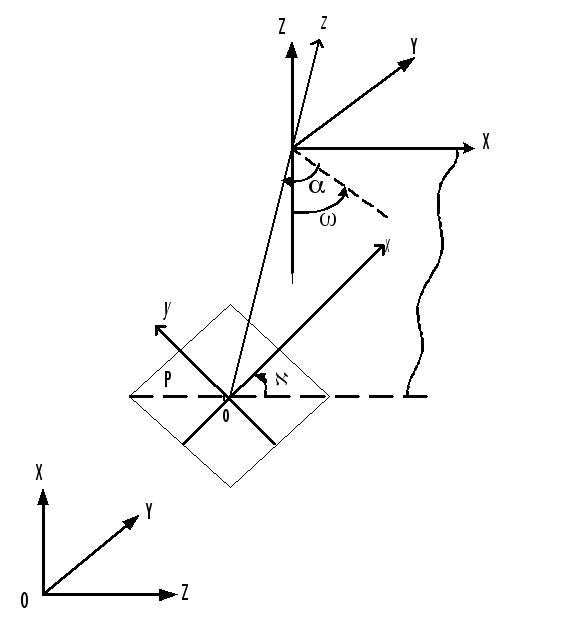
Рис.1.2.1

Значение элементов a_ij матрицы А можно получить путем последовательного перемножения матриц, составленных для последовательных поворотов системы координат объекта ОХYZ на углы ,  и .

В результате поворота системы координат ОХYZ или, что то же самое, системы координат SXYZ система SXYZ преобразуется в систему координат SX’Y’Z’ (рис.1.2.2).

Рис.1.2.2

В соответствии с выражением (1.2.1) матрица

.

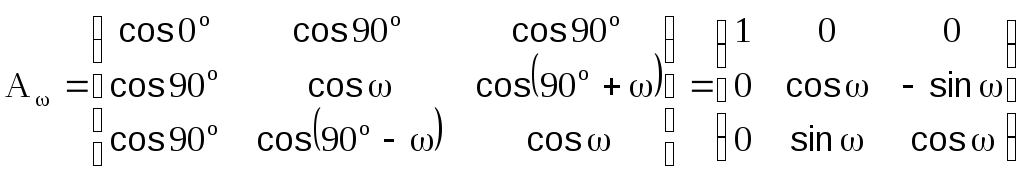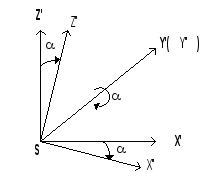В результате поворота на угол система координат SX’Y’Z’ преобразуется в систему координат SX”Y”Z” (рис.1.2.3).

Рис.1.2.3

В соответствии с выражением (1.2.1) матрица

.

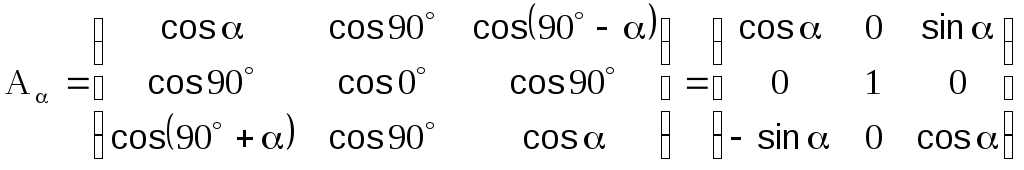В результате поворота системы координатSX”Y”Z” на угол  эта система преобразуется в систему координат снимка Sxyz (рис.1.2.4).

Рис.1.2.4

В соответствии с выражением (1.2.1) матрица

.

В результате перемножения матриц

,

получим значения элементов a_ij , как функции углов , и :

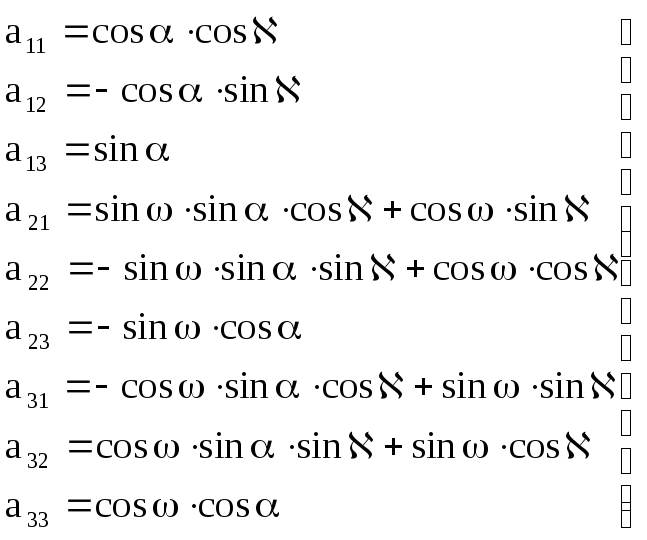(1.2.2);

Если известны значения направляющих косинусов aij, то из выражений (1.2.2) можно получить значения углов ,,.

(1.2.3).

2. Формулы связи координат соответственных точек снимка и местности.

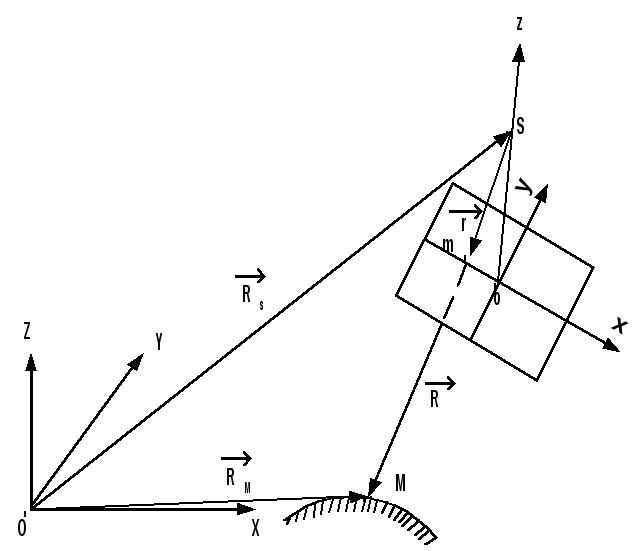
Рис.1.3.1

Пусть из точки S получен снимок Р, на котором точка М местности изобразилась в точке m. Найдем зависимости между координатами этих точек. Положение точки М местности в системе координат объекта OXYZ определяет вектор . Вектор определяет положение центра проекции S в системе координат объекта OXYZ.

Векторы и определяют собственно положение точек m и М относительно центра проекции S.

Из рис.1.3.1 следует, что

(1.3.1)

Векторы коллинеарные, поэтому можно записать, что

, (1.3.2)

где N-скалярная величина.

С учетом (1.3.2) выражение (1.3.1) имеет вид

; (1.3.3)

В координатной форме выражение (1.3.3) имеет вид

;

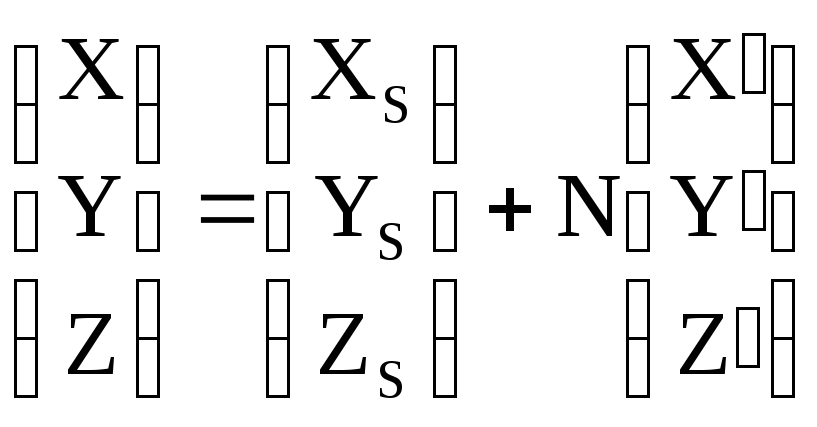или

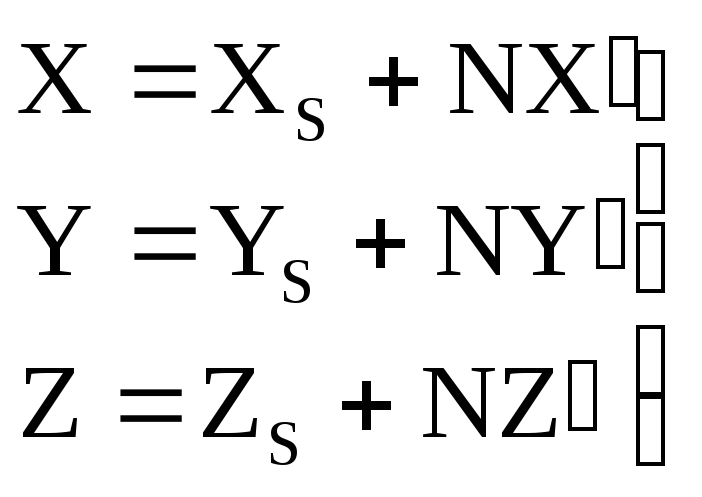. (1.3.4)

В выражении (1.3.4):

X,Y,Z-координаты точки М в системе координат объекта,

координаты центра проекции S в системе координат объекта; координаты векторав системе координат объекта.

; (1.3.5)

где А-матрица преобразования координат, элементы a_ij которой определяются по значениям угловых элементов внешнего ориентирования снимка ,,.

Из третьей формулы выражения (1.3.4) следует, что

.

Подставив значение N в первые две формулы выражения (1.3.4) получим формулы связи координат соответственных точек местности и снимка:

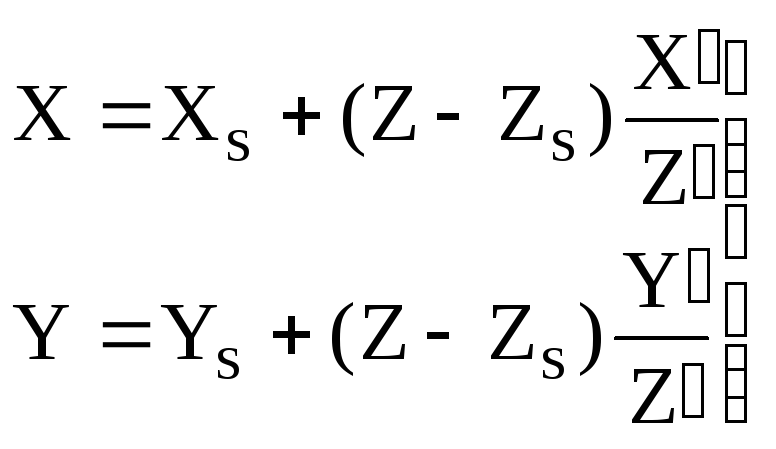; ( 1.3.6)

которые с учетом (1.3.5) имеют вид

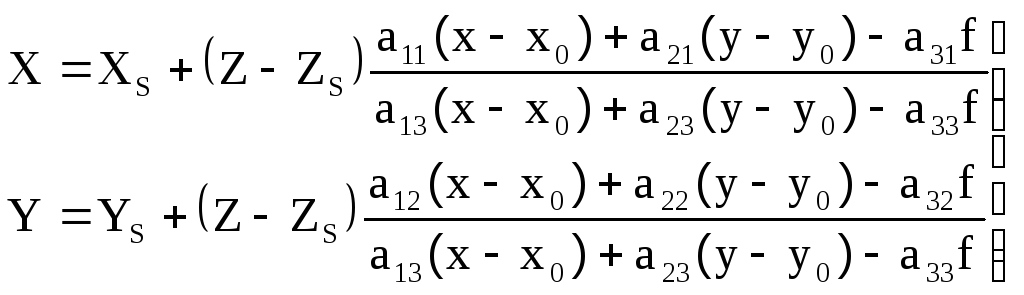; (1.3.7)

Из формул (1.3.6) следует, что координаты точки местности по снимку можно получить координатам ее изображения на снимке, если известны элементы внутреннего и внешнего ориентирования снимков и известна высота Z этой точки.

Найдем теперь формулы связи координат соответственных точек снимка и местности, которые позволят вычислить координаты изображения точки на снимке в системе координат снимка по координатам соответственной точки местности, определенным в системе координат объекта OXYZ.

Из выражения (1.3.3) следует, что

. (1.3.8)

В координатной форме выражение (1.3.8) имеет вид

;

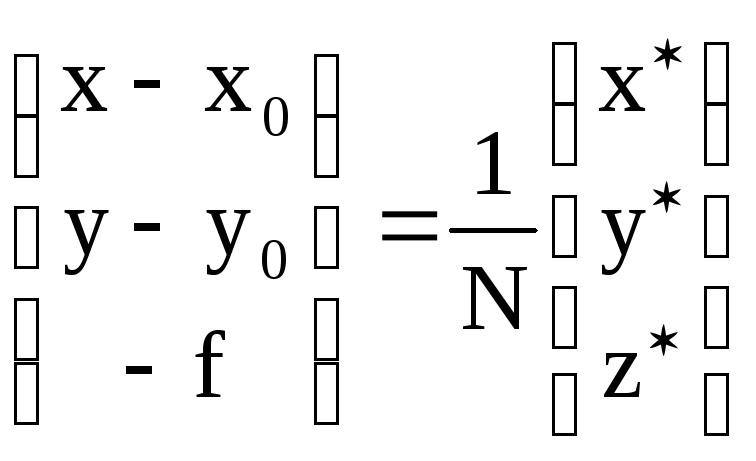или

; (1.3.9)

В выражении (1.3.9) x,y –координаты изображения точки местности m в системе координат снимка Sxyz.

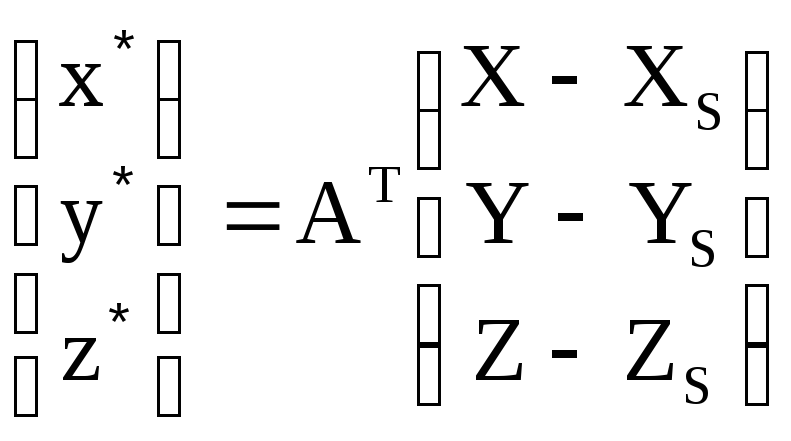; (1.3.10)

Из третьего выражения (1.3.9) следует, что

.

Подставив значение в первые два уравнения выражения (1.3.9), получим формулы связи координат соответственных точек снимка и местности.

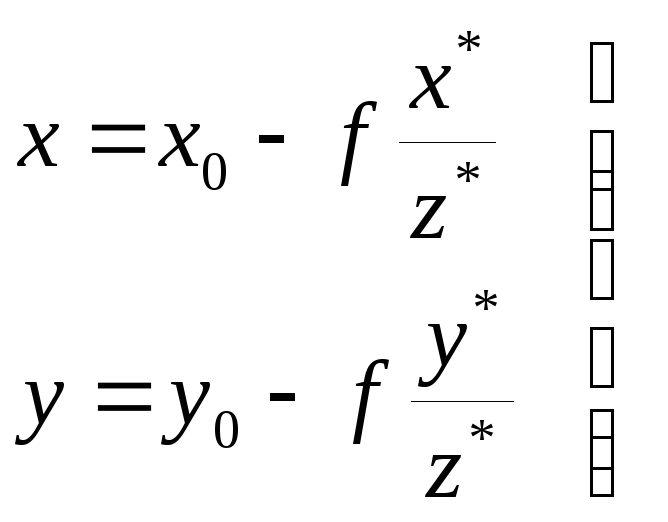, (1.3.11)

которые с учетом (1.3.10) имеют вид

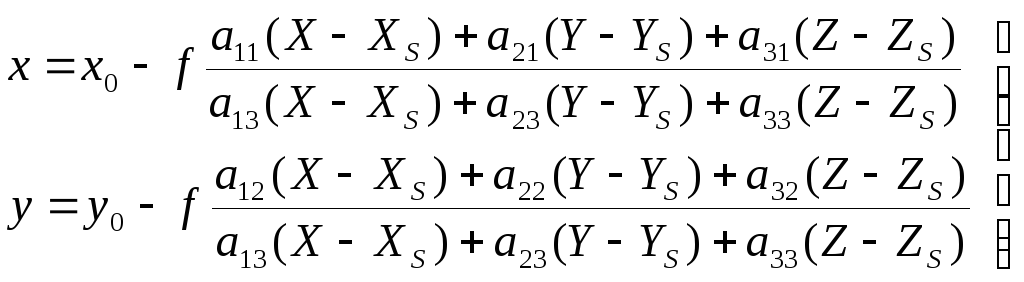. (1.3.12)

Формулы (1.3.12) в фотограмметрии часто называют уравнениями коллинеарности.

2. Формулы связи координат соответственных точек местности и горизонтального снимка.

У горизонтального снимка угловые элементы внешнего ориентирования ===0. Будем считать, что координаты главной точки снимка x₀=y₀=0.

В этом случае

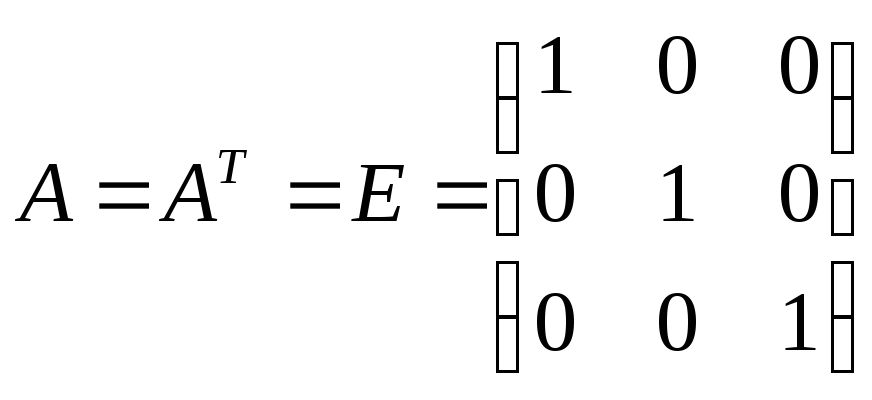. (1.4.1)

Формулы связи координат (1.3.6) и (1.3.12) при этом будут иметь вид

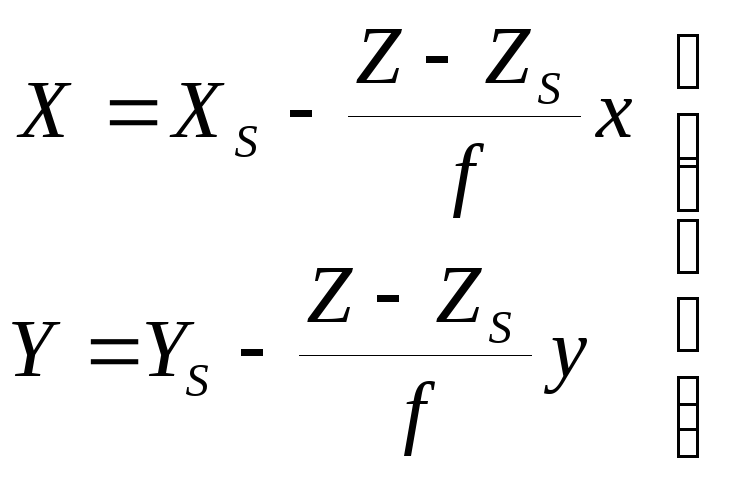, (1.4.2)

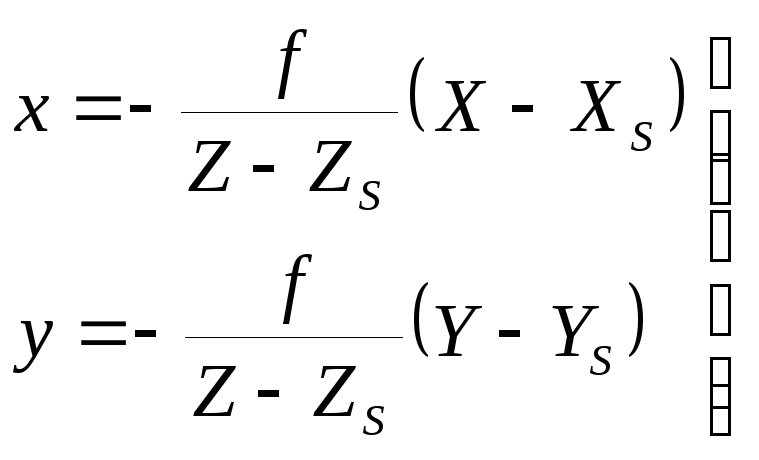. (1.4.3)

Если в качестве начала системы координат объекта OXYZ выбрать центр проекции S, то Xs=Ys=Zs=0, а формулы (1.4.2) и (1.4.3) примут вид:

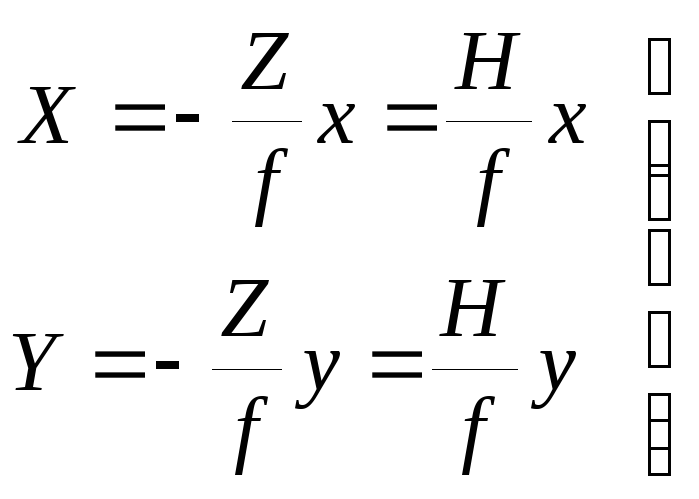; (1.4.4)

. (1.4.5)

( H = -Z – высота фотографирования над определяемой точкой)

Из формул (1.4.4) и (1.4.5) следует, что горизонтальным снимком горизонтальной местности можно пользоваться как планом масштаба

.

2. Определение элементов внешнего ориентирования снимка по опорным точкам (обратная фотограмметрическая засечка)

Опорной точкой будем называть точку, опознанную на местности и на снимке, геодезические координаты которой на местности известны.

Для определения элементов внешнего ориентирования снимка воспользуемся уравнениями коллинеарности (1.3.12), которые представим в виде

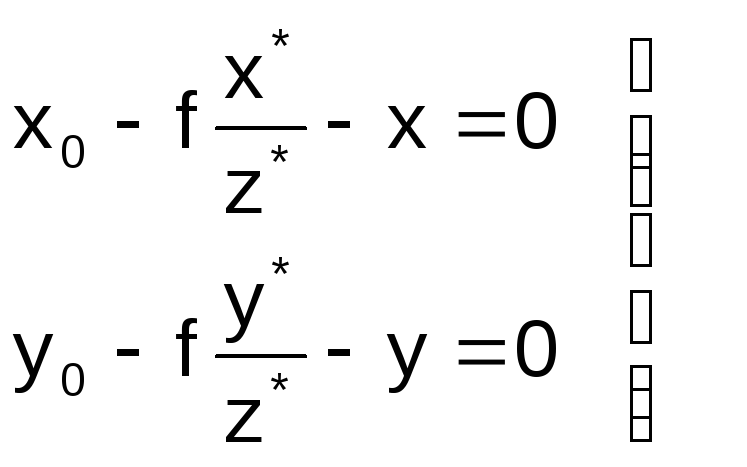; (1.5.1)

где

;

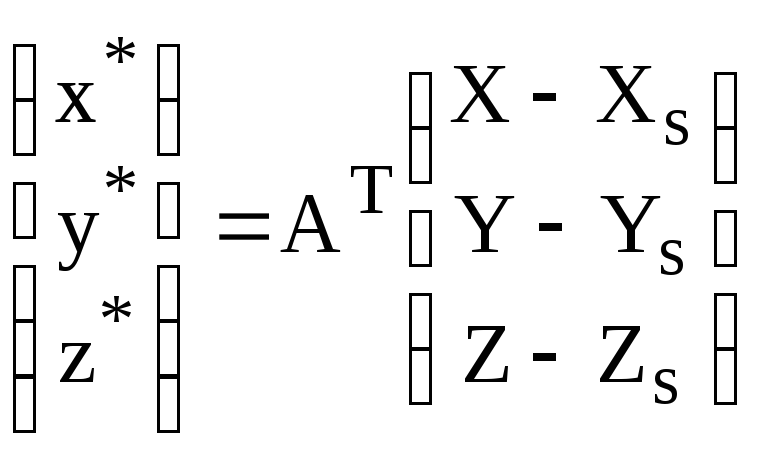или

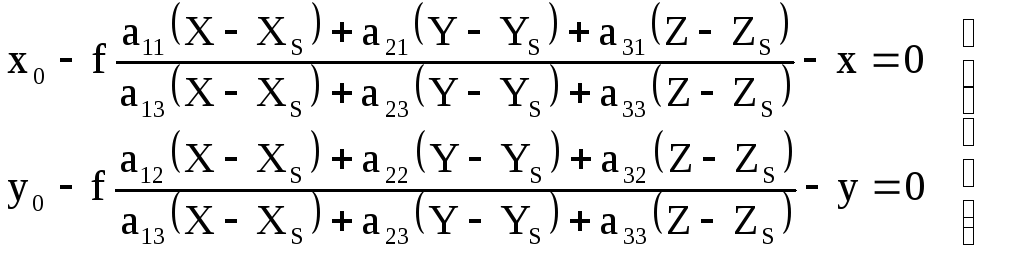. (1.5.2)

Если на снимке измерены координаты изображений опорных точек, то каждая опорная точка позволяет составить 2 уравнения (1.5.2), в которых известны значения координат х,у изображения опорной точки в системе координат снимка Sxyz, геодезические координаты опорной точки в системе координат объекта OXYZ и элементы внутреннего ориентирования снимка f,x₀,y₀.

Неизвестными величинами в уравнениях (1.5.2) являются 6 элементов внешнего ориентирования снимка Xs, Ys, Zs, , , .

Следовательно, для определения 6 неизвестных элементов внешнего ориентирования снимка достаточно иметь не менее 3 опорных точек. При этом опорные точки на местности не должны располагаться на одной прямой. Если имеются 3 опорные точки, координаты изображений которых на снимке измерены, можно составить систему из 6 уравнений (1.5.2) с 6 неизвестными. В результате решения этой системы уравнений можно найти значения элементов внешнего ориентирования снимка.

В связи с тем, что уравнения (1.5.2) нелинейные, решение системы уравнений непосредственно достаточно сложно, поэтому систему уравнений (1.5.2) решают методом приближений.

Для этого уравнения (1.5.2) приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок.

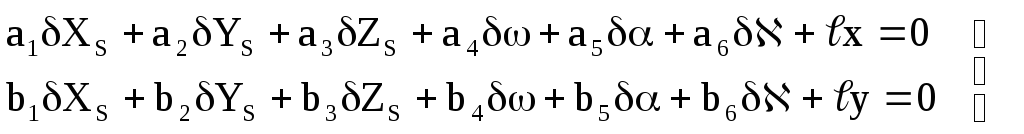. (1.5.3)

В уравнениях (1.5.3):

Xs, … , - поправки к приближенным значениям неизвестных элементов внешнего ориентирования снимка Xs⁰,…,⁰;

a_i, b_i – частные производные от уравнений (1.5.2) по соответствующим аргументам (например, коэффициент а₄ является частной производной от первого уравнения (1.5.2) по аргументу ,то есть);

ℓх, ℓу – свободные члены.

Значения коэффициентов уравнений (1.5.3) a_i, b_i вычисляются по известным значениям координат точек снимка и местности х,у и X,Y,Z, известным значениям элементов внутреннего ориентирования снимка f,x₀,y₀ и приближенным значениям неизвестных Xs⁰,…,⁰.

Свободные члены ℓх, ℓу вычисляются по формулам (1.5.2) таким же образом.

В результате решения системы уравнений поправок (1.5.3) находят поправки к приближенным значениям неизвестных и вычисляют уточненные значения неизвестных.

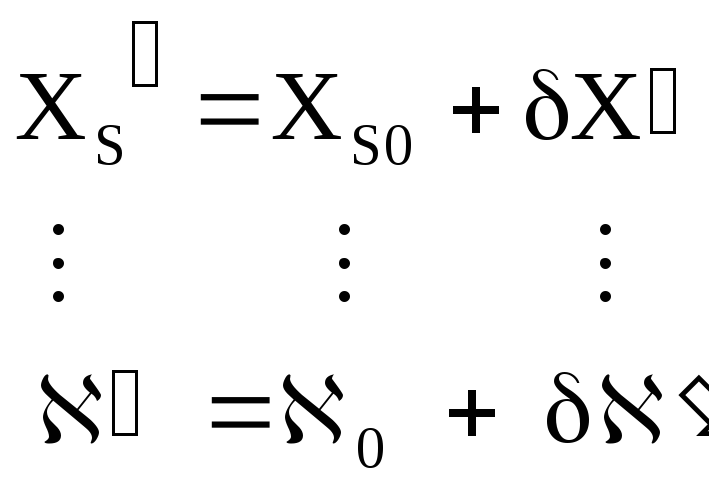
По уточненным значениям неизвестных повторно составляют уравнения поправок (1.5.3) и решают полученную систему уравнений.

Решения повторяют до тех пор, пока величины поправок, найденные в результате решения, не станут пренебрежимо малыми.

В случае если на снимке измерено более трех изображений опорных точек, то для каждой точки составляют уравнения поправок вида:

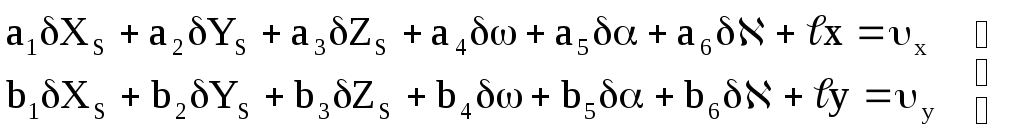; (1.5.4)

Решение полученной системы уравнений (1.5.4) производят методом приближений, по методу наименьших квадратов (под условием V^TV = min).