
Laboratornaya_rabota_GF-3_1_dop
.pdf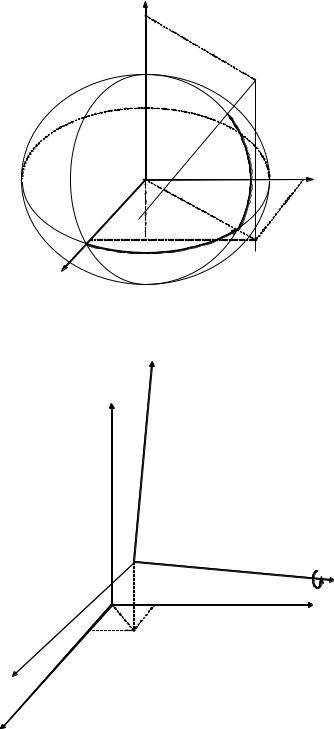
Лабораторная работа № 1
Преобразования координат из одной системы в другую носят строго выраженные математические зависимости и в общем виде представлены на (Рис. 1, Рис. 2)
Z
ZQ
H Q
Начальный |
N |
меридиан |
YQ |
|
|
|
Y |
|
eN |
|
L |
X
Рис. 1 Связь прямоугольных прямолинейных и криволинейных геоцентрической координат
ZA
 ω Z
ω Z
ZB
Zo 
YA
Yo |
ω Y |
Xo |
YB |
|
XA 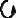 ω X
ω X
XB
Рис. 2 Связь двух геоцентрических систем координат
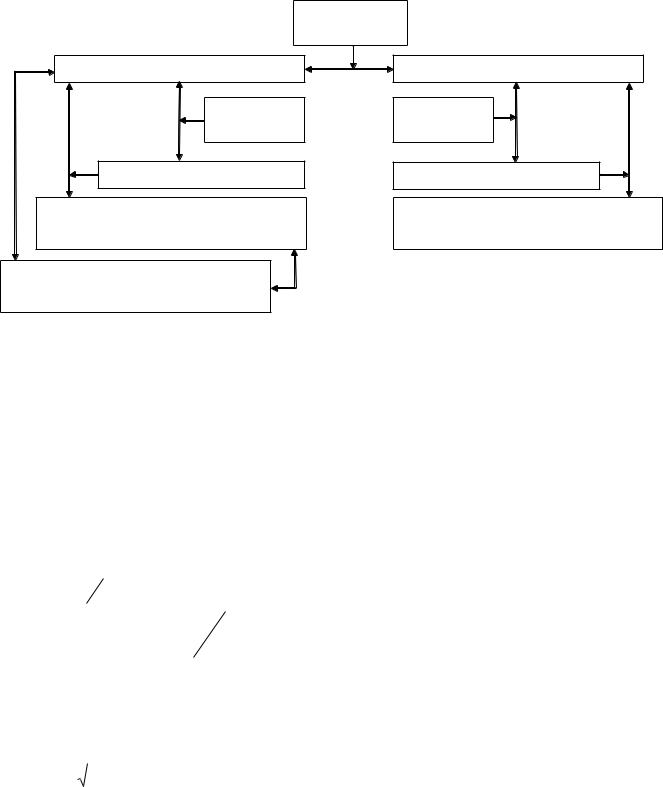
Параметры
преобразования
СК1, Геоцентрические (XYZ) |
СК2, Геоцентрические (XYZ) |
Параметры
эллипсоида
Геодезические (BLH)
Параметры
эллипсоида
Геодезические (BLH)
Топоцентрические (XYZ) в системе |
Топоцентрические (XYZ) в системе |
точки Qi |
точки Pi |
Топоцентрические (XYZ) в системе |
|
точки Qj |
|
Связь пространственных прямоугольных XYZ и эллипсоидальных
|
|
|
координат BLH 1 |
|
|
Связь выражается следующими формулами: |
|
||||
X = ( N + H ) cos B cos L; |
|
||||
Y = ( N + H ) cos B sin L; |
-1 |
||||
æ æ |
2 ö |
ö |
sin B; |
||
|
|||||
Z = ç ç 1- e |
÷ |
N + H ÷ |
|
||
è è |
ø |
ø |
|
|
|
Обратные преобразования осуществляются по следующим формулам:
tgL = |
Y |
X |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
D - e |
2 |
|
ö |
|
|
||||
ctgB |
ç |
|
N cos B÷ |
|
; |
||||||
= è |
|
|
|
|
ø |
Z |
|||||
H = |
Dsec B - |
N; |
|
|
|
|
|||||
|
|
|
|
|
|||||||
Где |
|
|
|
|
|
|
|
|
|
|
|
D = ( N + |
H ) cos B; |
|
|
||||||||
N = |
|
|
|
a |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
e2 sin2 |
|
|
|
|||||
|
1- |
B |
|
|
|||||||
e2 = |
2α |
- α 2 |
|
|
|
|
|
|
|
||
X, Y, Z – геоцентрические прямоугольные координаты; B, L – геодезические широта и долгота точки;
H – геодезическая высота точки;
N - радиус кривизны первого вертикала;
-2
-3

D - экваториальное расстояние; е – эксцентриситет эллипсоида.
Во время преобразований из пространственных прямоугольных XYZ в эллипсоидальные координаты BLH, необходимо соблюдать соответствие принятой системы координат используемому эллипсоиду.
D = 
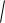 X 2 + Y 2 ;
X 2 + Y 2 ;
Если D = 0; то
|
|
π Z |
|
|
|
|
|
|
|
|
H = Z sin B - a |
|
||||||||||
B = |
|
|
|
|
; |
L = |
0; |
1- e2 sin2 B |
||||||||||||||
2 |
|
Z |
|
|
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если D ¹ 0; при |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Y < 0, X > 0, то L = 2π − L0 ; |
|
|
|
|
||||||||||||||||||
Y < 0, X < 0, то L = π + L0 ; |
|
|
|
|
|
|
||||||||||||||||
Y > 0, X < 0, то L = π - L0 ; |
|
|
|
|
|
|
||||||||||||||||
Y > 0, X > 0, то L = L0 ; |
|
|
|
|
|
|
||||||||||||||||
Y = |
0, |
|
|
|
X > 0, |
то |
L = 0; |
|
|
|
|
|
|
|||||||||
Y = 0, X < 0, то L = π ; |
|
|
|
|
|
|
||||||||||||||||
где L0 = |
|
|
|
|
|
|
æ |
Y ö |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
arcsinç |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
è |
D ø |
|
|
|
|
|
|
|
|
|
|
|
|
||
Если Z = 0; то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
B = |
0; |
|
|
|
H = D − |
a; |
|
|
|
|
|
|
|
|||||||||
Если Z ¹ 0; |
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
Z ö |
|
|
|
e2a |
|
r = |
|
|
X |
|
2 + Y 2 |
+ Z 2 ; |
; |
p |
= |
|||||||||||||
|
|
|
c = arcsinç |
÷ |
2r |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
r ø |
|
|
|
||
Реализуют итеративный процесс, используя вспомогательные величины
|
|
æ |
|
psin(2b) |
ö |
|
|
|
|
|||||
s1 = |
0; b = c + s1; s2 = |
arcsinç |
|
|
|
|
|
|
|
÷ |
; |
ε = |
s2 - s1 |
; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
|
|
ç |
1- e |
2 |
sin |
2 |
÷ |
|
|
|
|
|||
|
|
è |
|
|
b ø |
|
|
|
|
|||||
Если ε меньше установленного допуска на изменение координат, то
B = b. H = D cos B + Z sin B - a
 1- e2 sin2 B
1- e2 sin2 B
-4
(5
(6
-7
-8
-9
-10
При перевычислении прямоугольных геоцентрических координат из одной системы в другую, например:
-из ПЗ-90 в WGS-84 и обратно;
-из ПЗ-90 в СК-42 и обратно; применяют следующие формулы:
é |
X p |
ù |
|
é |
1 |
|
wz |
|
- wy ù é |
Ap ù |
é dX o ù |
|
|
|||||||
ê |
Y |
p |
ú |
= |
(1+ dm)ê |
- w |
z |
1 |
|
w |
x |
ú ê |
B |
ú |
+ ê |
dY |
ú |
; |
-11 |
|
ê |
Z |
ú |
|
ê |
w |
|
- w |
|
|
ú ê |
C |
p ú |
ê |
o ú |
|
|||||
ê |
p |
ú |
|
ê |
y |
|
x |
1 |
ú ê |
ú |
ê |
dZ |
ú |
|
|
|||||
ë |
|
û |
|
ë |
|
|
|
|
|
û ë |
|
p û |
ë |
|
o û |
|
|
|||
|
где |
|
Ap Bp Cp − первая система координат; |
|
|
|
||||||||||||||
Xp Yp Zp - вторая система координат;
dXo dYo dZo - линейные элементы вектора смещения начала второй системы координат относительно первой;
w x w y w z - угловые элементы вращения осей второй системы (выражены в радианной мере) для обеспечения их параллельности с осями первой;
dm - масштабная поправка выражает различие линейных масштабов двух систем координат;
Преобразования геодезических координат из одной системы осуществляют и по прямым формулам
BБ = BА + B; |
|
LБ = LА + D L; |
-12 |
H Б = H А + D H; |
|

|
ρ |
" |
|
N |
æ |
N |
2 |
ö |
|
D e |
2 |
|
D B = |
|
[ |
e2 sin B cos BD a + ç |
|
+ 1÷ |
N sin B cos B |
|
- |
||||
|
|
|
|
2 |
|
|
||||||
|
(M + |
H ) |
|
a |
ç |
a |
÷ |
2 |
|
|
||
|
|
è |
|
ø |
|
|
||||||
|
- |
(D x cos L + |
D y sin L)sin B + D z cos B] - |
|
|
|
|
|
|
||||||||||||||||||||
|
- ϖ x sin L(1+ |
e2 cos 2B) + ϖ |
y cos L(1+ |
|
e2 cos 2B) - |
ρ "me2 sin B cos B; |
|
||||||||||||||||||||||
D L = |
|
|
|
ρ " |
|
(- D xsin L + |
D y cos L) + |
tgB(1- e2 )(ϖ |
x cos L + ϖ y sin L) - ϖ |
z ; |
|||||||||||||||||||
|
(M + |
H ) cos B |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
D H = |
- |
a |
D a + N sin 2 |
B |
D a2 |
|
+ |
(D x cos L + |
D y sin L) cos B + D z sin B - |
-13 |
|||||||||||||||||||
N |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
ϖ |
|
|
|
|
|
|
|
ϖ |
y |
|
|
|
|
ö |
æ |
a2 |
|
ö |
|
|
||
|
- |
Ne2 sin B cos Bç |
|
|
x |
sin L - |
|
|
|
|
cos L |
÷ |
+ ç |
|
|
+ |
H ÷ m; |
|
|||||||||||
|
|
" |
|
|
|
" |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
ç |
ρ |
|
|
|
|
|
|
ρ |
|
|
|
|
÷ |
ç |
N |
|
÷ |
|
|
||||
M = |
|
|
|
|
|
è |
|
|
|
− 2 ; |
|
|
|
a(1- |
|
ø |
è |
|
ø |
D a = aБ - aА ; |
|
||||||||
a(1- e2 )(1- e2 sin 2 B) |
|
N = |
e2 sin 2 B)− 2 |
; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
D e2 |
= |
e2 Б - e2 А ; |
a = |
a |
Б |
+ a |
А |
; |
|
e2 |
= |
e2 |
Б |
+ e2 А |
; |
ρ " = 206264,8062; |
|
||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Топоцентрические системы координат
Z
Y
L
Рис. 3 Связь геоцентрической экваториальной OXYZ и топоцентрической
горизонтной Q1XтопYтопZтоп систем координат
é - sin Bcos L |
- sin L |
cos Bcos Lù |
||
А = ê |
- sin Bsin L |
cos L |
cos Bsin Lú |
|
ê |
cos B |
0 |
sin B |
ú |
ê |
ú |
|||
ë |
|
|
|
û |
Вычисление геоцентрических координат из топоцентрических
é |
X Г ù |
|
é |
X Г ù |
|
||
ê |
Y |
ú |
= |
ê |
Y |
ú |
+ |
ê |
Z |
Г ú |
|
ê |
Z |
Г ú |
|
ê |
ú |
|
ê |
ú |
|
||
ë |
|
Г û 2 |
|
ë |
|
Г û 1 |
|
é XТ ù
Aêê YТ úú êë ZТ úû 2
Обратное преобразование выполняется:
é |
XТ ù |
|
æ é |
X Г ù |
|
é |
X Г ù |
ö |
|||
ê |
|
ú |
Т |
ç ê |
|
ú |
- |
ê |
|
ú |
÷ |
ê |
YТ ú |
= A |
ç ê |
YГ ú |
ê |
YГ ú |
÷ |
||||
ê |
Z |
ú |
|
ç ê |
Z |
ú |
|
ê |
Z |
ú |
÷ |
ë |
|
Т û 2 |
|
è ë |
|
Г û 2 |
|
ë |
|
Г û |
1 ø |
-14
-15
|
|
|
|
Приложение 1 |
|
|
|
Характеристики основных эллипсоидов |
|||
|
|
|
Большая полуось, |
Квадрат |
|
№ п/п |
Название эллипсоида |
эксцентриситета |
|||
м |
|||||
|
|
|
e2 103 |
||
1 |
ОЗЭ ПЗ-90 |
|
6378136 |
6,694366199 |
|
2 |
ОЗЭ ПЗ-85 |
|
6378136 |
6,694384999 |
|
3 |
ОЗЭ WGS-84 |
|
6378137 |
6,694381317 |
|
4 |
ОЗЭ WGS-72 |
|
6378135 |
6,694317783 |
|
5 |
ОЗЭ WGS-60 |
|
6378155 |
6,693421623 |
|
6 |
Красовского |
|
6378245 |
6,693421623 |
|
7 |
Хейфорда (1909) |
|
6378388 |
6,722670022 |
|
8 |
Бесселя (1841) |
|
6377397 |
6,674434883 |
|
9 |
Кларка (1866) |
|
6378206 |
6,768628177 |
|
10 |
Кларка (1880) |
|
6378249 |
6,803395565 |
|
11 |
Австралийский |
|
6378160 |
6,695662461 |
|
12 |
Эвереста (1830) |
|
6377276 |
6,637663782 |
|
13 |
Фишера |
|
6378155 |
6,693421623 |
|
Элементы трансформирования из ПЗ-90 в другие системы координат |
|
|||||||
Геодезические |
Линейные элементы, |
|
Угловые элементы |
|
||||
системы |
|
м |
|
|
|
(секунды дуги) |
dm |
|
координат |
X |
Y |
Z |
|
wx |
wy |
w |
|
СК-42 |
-25 |
141 |
80 |
0 |
|
0,35 |
0,66 |
|
WGS-84 |
0 |
0 |
-1 |
0 |
|
0 |
0,2 |
|
Задание
Схема исходной сети и исходные данные
B |
D |
F |
1 |
2 |
3 |
4 |
A |
C |
E |
1 |
2 |
3 |
4 |
|
B |
D |
F |
|
|
A |
|
C |
E |
|
|
|
|
№ п/п |
B |
L |
H |
A |
50.0+i/20 |
35.0+i/20 |
100 |
B |
51.0+i/20 |
35.0+i/20 |
105 |
C |
50.0+i/20 |
36.0+i/20 |
110 |
D |
51.0+i/20 |
36.0+i/20 |
95 |
E |
50.0+i/20 |
37.0+i/20 |
120 |
F |
51.0+i/20 |
37.0+i/20 |
115 |
1 |
50.5+i/20 |
35.0+i/20 |
150 |
2 |
50.5+i/20 |
35.8+i/20 |
135 |
3 |
50.5+i/20 |
36.4+i/20 |
140 |
4 |
50.5+i/20 |
37.0+i/20 |
145 |
Параметры эллипсоида указаны в приложении №2 (7000+i, i – номер по журналу, 7017 заменить номером 7027); Параметры преобразования из СК1 в СК2 – строка с параметрами соответствует номеру строки
втаблице приложения 3.
1.Вычислить координат всех пунктов B,L,H;
2.Преобразовать B,L,H в X,Y,Z;
3.Преобразовать геоцентрические {X,Y,Z}ск1 в {X,Y,Z}ск2
4.Преобразовать {X,Y,Z}ск2 в B,L,H с уровнем сходимости 0.0003”;
5.Сравнить B,L,H п.1 и п.3;
6.Вычислить топоцентрические координаты {X,Y,Z}Т всех точек в системах координат всех точек.
7.Преобразовать все{X,Y,Z}Т в полярные координаты {S,A,z}

Приложение 2
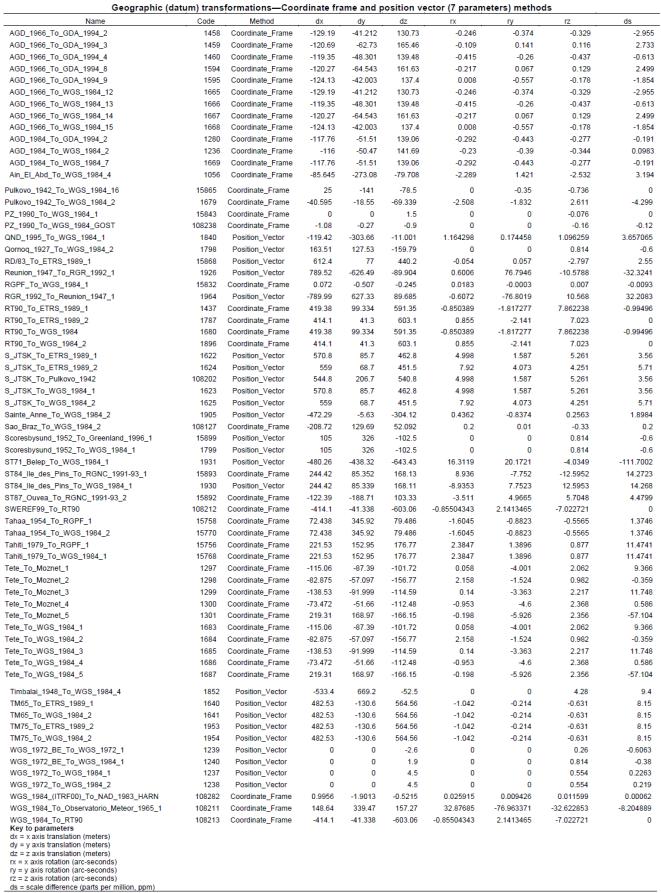
Приложение 3
