Примеры выполнения заданий лабораторной работы
1.
Вычислить производную функции
,
еслиа)
(x)
= ctg
x,
(x)
= log4x,
k
= 3, m
= 2, n
= 2; б)
(x)
= arc
sin
x,
(x)
= 2x5,
k
= 2, m
= 3, n
= 1.
Решение.
а)
Дано:
.
Согласно правилу дифференцирования дроби:
=
.
Имеем:
u(x)
= ctg(log4x),
v(x)
=
.
Находим производные u (x) и v (x) согласно правилу дифференцирования сложных функций:
u
(x)
=
;
v
(x)
=
.
Подставляем функции u(x), v(x) и их производные в формулу производной дроби:
у
(х)
=
=
.
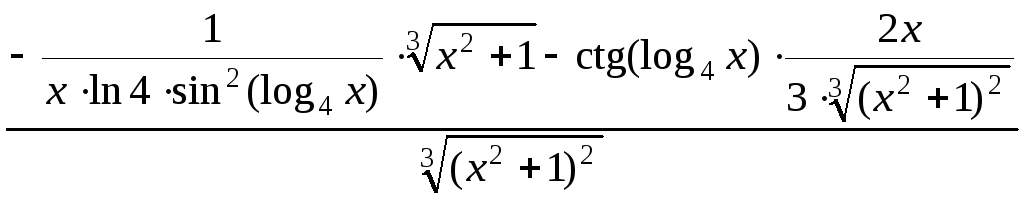б)
Дано:
.
Согласно правилу дифференцирования произведения:
у
(х)
= (u(х)v(х))
=
u
(х)v(х)
+ u(х)v
(х).
Имеем:
u(x)
= arc sin 2x5,
v(x)
=
.
Находим производные u (x) и v (x) согласно правилу дифференцирования сложных функций:
u
(x)
=
;
v
(x)
=
.
Подставляем функции u(x), v(x) и их производные в формулу производной произведения:
у
(х)
=
.
Ответ:
а)
у
(х)
=
;
б)
у
(х)
=
.
2.
Составить уравнения касательной и
нормали к графику функции y
(x)
=
в точкеx
= ,
где r
= 3,
= – 13,
= 5.
Решение.
Дано:
.
Уравнение касательной к графику функцииу
= у(х)
в точке М(х0;
у0),
где y0
= y(x0):
y
= y0
+ у'(х0)(x
– x0).
Уравнение нормали к графику функции у
= у(х)
в точке М(х0;
у0):
y
= y0
–
(x
– x0).
Поскольку
х0
= 5, то получаем
= 1/2.
Находим
производную
=
,
т.е.у
(5) = 49/260.
Записываем
уравнение касательной к кривой у
= у(х)
в точке М(5;
1/2): y
= 0,5 +
(x
– 5);
записываем уравнение нормали в точке
М(5;
1/2): y
= 0,5 –
(x
– 5).
Ответ:
y
= 0,5 +
(x
– 5)
– уравнение касательной;
y
= 0,5 –
(x
– 5)
– уравнение нормали.
3.
Составить
уравнения касательной и нормали к
графику функции y
= y(x),
заданной параметрически:
в точкеМ(х(t0);
y(t0)),
где x(t)
=
5
–
2ctg
t,
y(t)
=
1
+
cos
2t
, t0
= /4.
Решение.
Дано:
Уравнение касательной к графику функцииу
= у(х)
в точке
М(х0;
у0),
где x0
= x(t0),
y0
= y(t0):
y
= y0
+ у'(х0)(x
– x0).
Уравнение нормали к графику функции
у = у(х)
в точке М(х0;
у0):
y
= y0
–
(x
– x0).
Поскольку t0 = /4, то получаем: x0 = x(/4) = 5 – 2ctg (/4) = 3, y0 = y(/4) = 1 + cos(/2) = 1.
Находим
производную
=
= –sin
2t
sin2t,
т.е. у
(x0)
= – sin(/2)sin2(/4)
= – 1/2.
Записываем
уравнение касательной к кривой у
=
у(х)
в
точке М(3;
1):
y
=
1
–
(x
–
3),
или у
=
2,5 – 0,5х;
записываем уравнение нормали в точке
М(3;
1): y
= 1 + 2(x
– 3), или y
= 2х
– 5.
Ответ: y = 2,5 – 0,5x – уравнение касательной;
y = 2x – 5 – уравнение нормали.
4.
Применяя правило Лопиталя, найти
,
если:а)
(x)
= x3
–
1, (x)
= ln
x,
a
= 1; б)
(x)
= x2,
(x)
= е2х,
a
= + .
Решение.
а)
Предел
в окрестности точких
= 1 имеет
неопределенность
.
Следовательно, для нахождения этого
предела можно использовать правило
Лопиталя (переход к пределу, определяемому
по правилу Лопиталя, будем обозначать
как
):
=
=
=
= 3.
б)
Предел
имеет неопределенность
,
следовательно,для
нахождения этого предела можно
использовать правило Лопиталя:
=
=
=
=
=
= 0.
Ответ: а) 3; б) 0.