
- •О.Ю. Горлова, в.И. Самарин
- •Лабораторная работа №1 Матрицы и определители
- •Задания
- •Справочный материал
- •12. Элементарные преобразования строк и столбцов матрицы:
- •15. Свойства определителей:
- •17. Матричный метод нахождения обратной матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 2 Системы линейных алгебраических уравнений
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 3 Векторы
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 4 Собственные значения и собственные векторы квадратной матрицы
- •Задание
- •Справочный материал
- •10. Идентификация собственных векторов и собственных значений матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 5 Прямая и плоскость
- •Задания
- •Справочный материал
- •1. Уравнения прямой на плоскости:
- •4. Уравнения плоскости:
- •7. Уравнения прямой в пространстве:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 6 Кривые второго порядка
- •Задания
- •Справочный материал
- •Гипербола
- •Парабола
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 7 Пределы и непрерывность функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 8 Дифференциальное исчисление функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Литература
- •Оглавление
- •Горлова Ольга Юрьевна,
Справочный материал
к 7-й лабораторной работе
Функция (числовая функция) у = у(х) – зависимость переменной у от переменной х, при которой каждому значению х
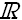 соответствует
единственное значение у;
независимая переменная х
называется аргументом
функции.
соответствует
единственное значение у;
независимая переменная х
называется аргументом
функции.
Числовая последовательность – функция, областью определения которой является множество натуральных чисел; числовая последовательность обозначается как {un}, n
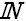 .
.
Монотонная числовая последовательность – возрастающая последовательность (т.е. последовательность {un}, в которой un un +1 для всех п) или убывающая последовательность (т.е. последовательность {un}, в которой un un +1 для всех п).
Ограниченная числовая последовательность – последовательность {un}, для которой существует такое число С
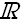 ,
что |un|
C
для всех n.
,
что |un|
C
для всех n.
Предел числовой последовательности {un} – такое конечное число А, что с ростом п величина |un – A| сколь угодно близко приближается к нулю, т.е. для любого сколь угодно маленького числа ε > 0, начиная с некоторого номера N (т.е. при n N) будет выполняться неравенство |un – A| < ε; обозначение предела числовой последовательности:
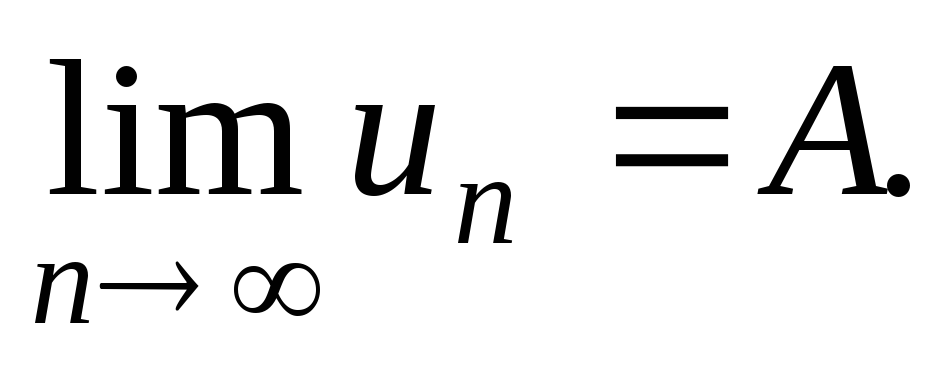
Теорема Вейерштрасса: если, начиная с некоторого номера N, последовательность монотонна и ограничена, то она имеет предел.
Сходящейся числовая последовательность – последовательность {un}, имеющая конечный предел; неограниченно возрастающая монотонная последовательность (обозначение:
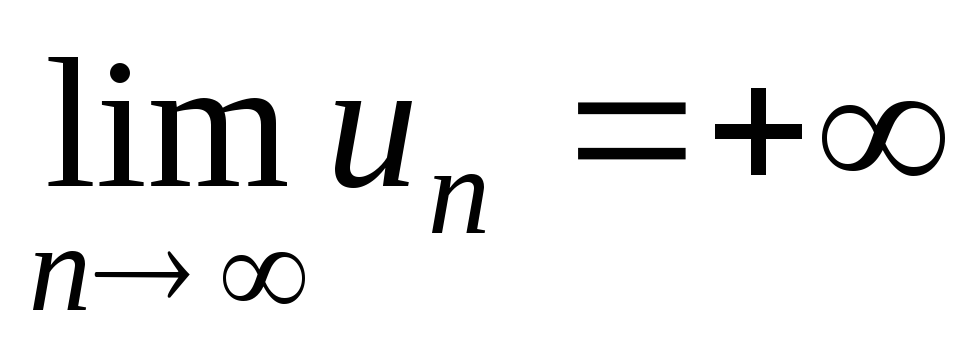 ),
неограниченно убывающая монотонная
последовательность (обозначение:
),
неограниченно убывающая монотонная
последовательность (обозначение:
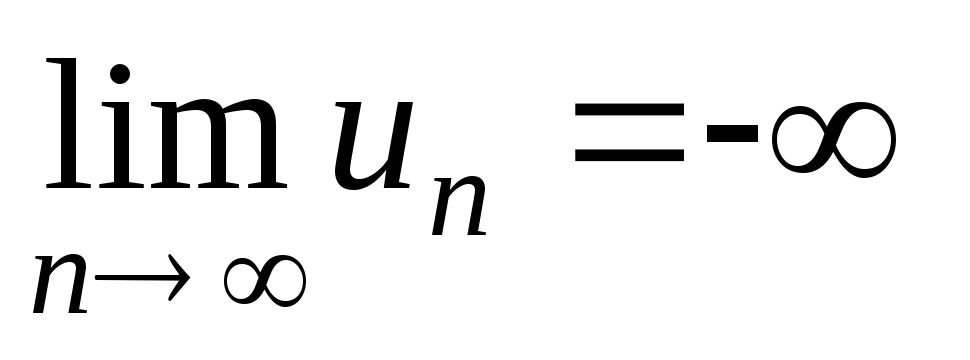 )
и последовательность, для которой
предела не существует, называется
расходящейся.
)
и последовательность, для которой
предела не существует, называется
расходящейся.
Бесконечно большие последовательности – последовательности {un}, для которых
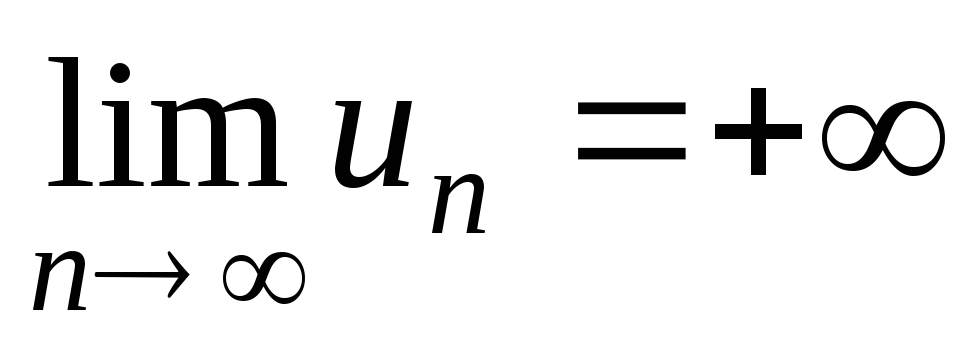 или
или
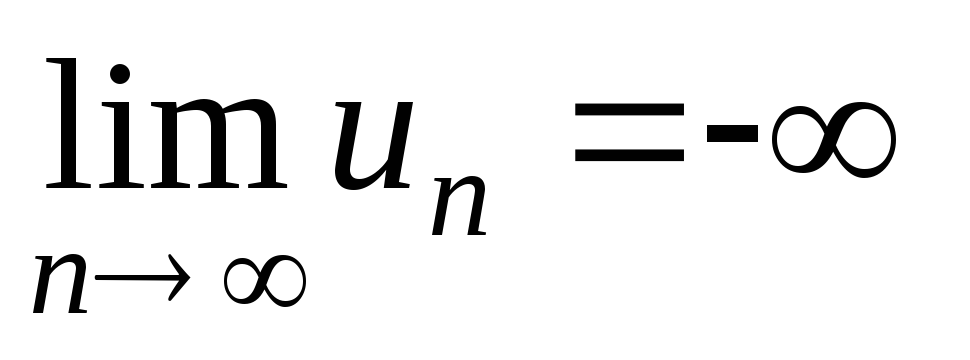 ;
обозначение бесконечно больших
последовательностей:
;
обозначение бесконечно больших
последовательностей:
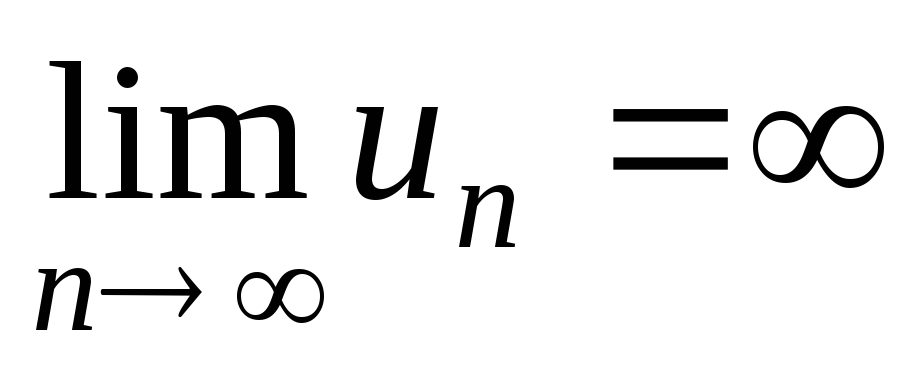 .
.
Бесконечно малые последовательности – последовательности {un}, для которых
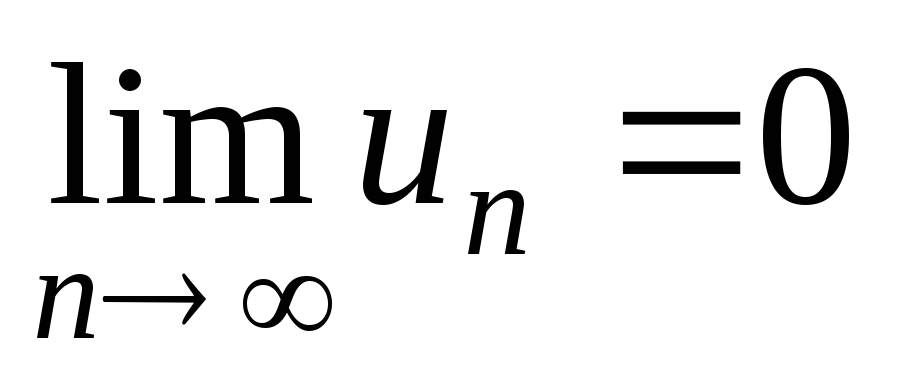 .
.
Предел функции у = у(х) в точке х = х0 – такое конечное число А, что для любой бесконечной последовательности точек {xn} на оси х, сходящейся к точке х = х0, т.е. когда
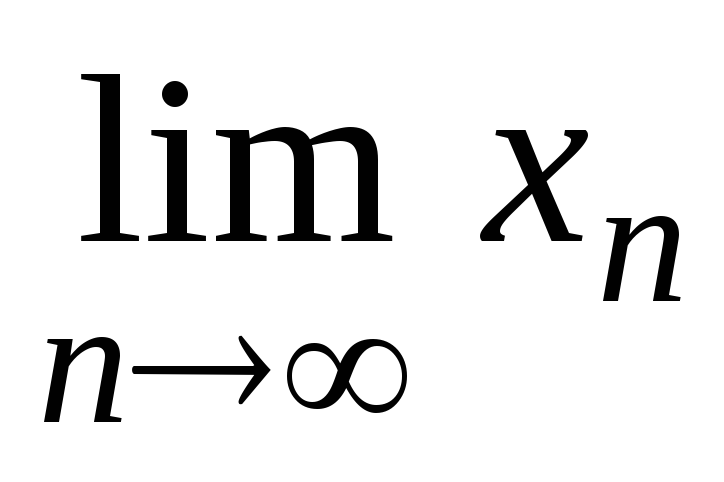 = х0,
соответствующая последовательность
{yn
= y(хn)}
сходится к точке y
= А,
т.е. когда
= х0,
соответствующая последовательность
{yn
= y(хn)}
сходится к точке y
= А,
т.е. когда
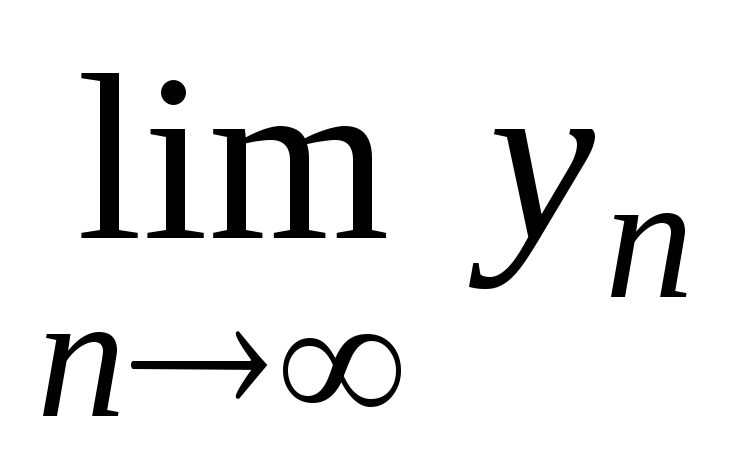 = А;
обозначение предела функции у
= у(х)
в точке х
= х0:
= А;
обозначение предела функции у
= у(х)
в точке х
= х0:
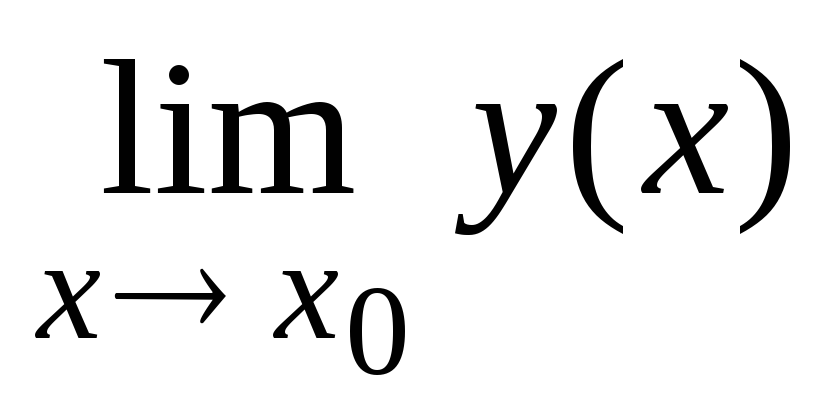 = А.
Число
А
называется
пределом функции
y
=
y(x)
при
х
+
∞, если с ростом х
значение
функции подходит как угодно близко к
А:
= А.
Число
А
называется
пределом функции
y
=
y(x)
при
х
+
∞, если с ростом х
значение
функции подходит как угодно близко к
А:
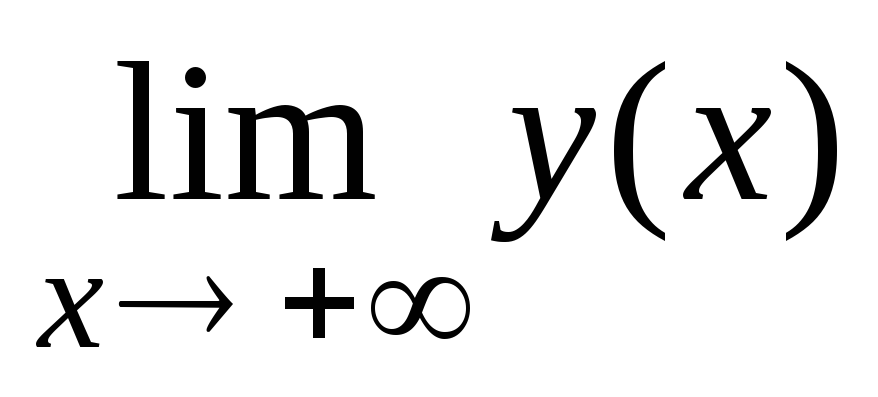 =
А;
если же при х
– ∞,
значение функции y
=
y(x)
стремится
к числу В,
то
=
А;
если же при х
– ∞,
значение функции y
=
y(x)
стремится
к числу В,
то
 =
В;
если
А
=
В,
то обозначение предела функции:
=
В;
если
А
=
В,
то обозначение предела функции:
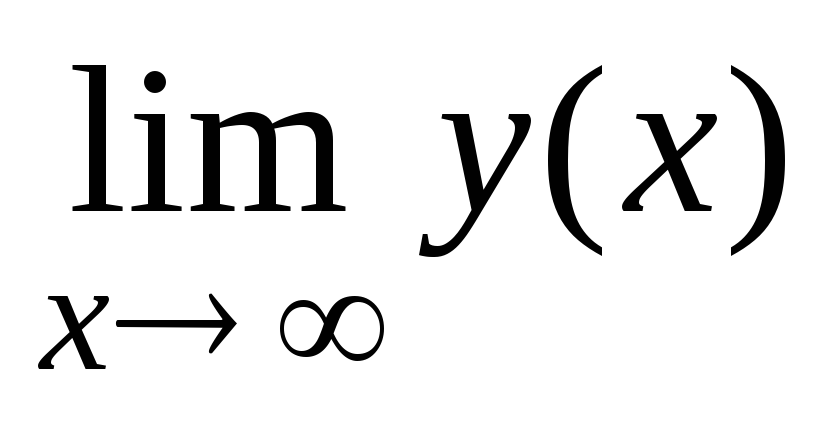 =
=
 =
А.
=
А.
Бесконечно большая – функция y= y(х), для которой
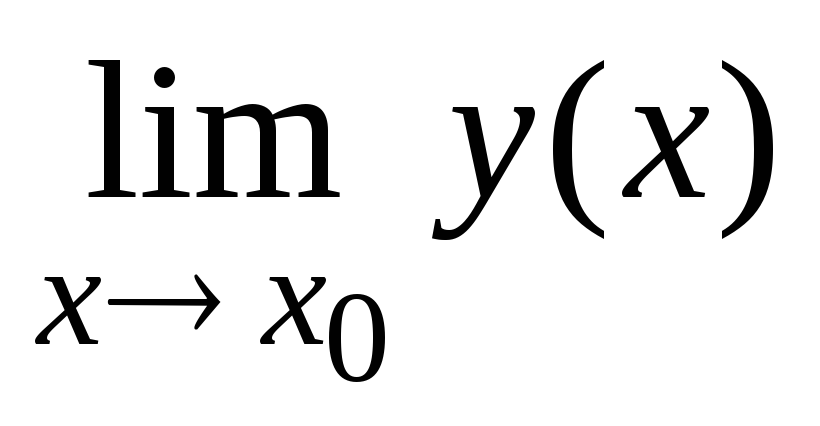 =∞,
где х0
– конечное число или ∞ (т.е. один из
символов + ∞, или – ∞).
=∞,
где х0
– конечное число или ∞ (т.е. один из
символов + ∞, или – ∞).
Бесконечно малая в окрестности точки х = х0 – функция y= y(х), для которой
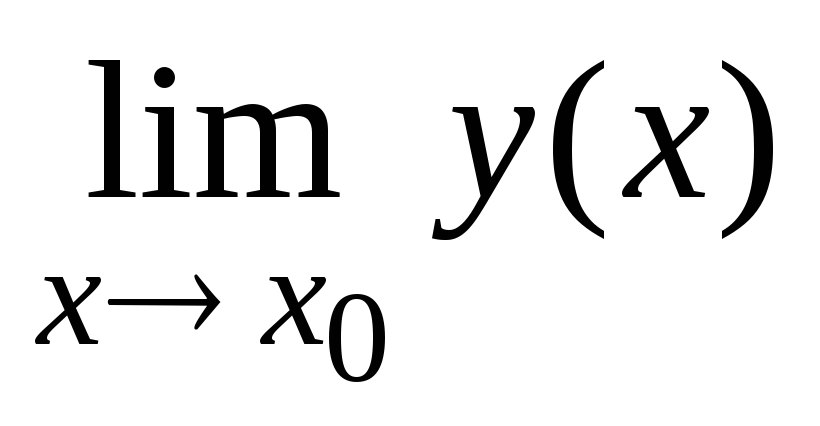 = 0,
где х0
– конечное число; бесконечно малая на
бесконечности – функция y=
y(х),
для которой
= 0,
где х0
– конечное число; бесконечно малая на
бесконечности – функция y=
y(х),
для которой
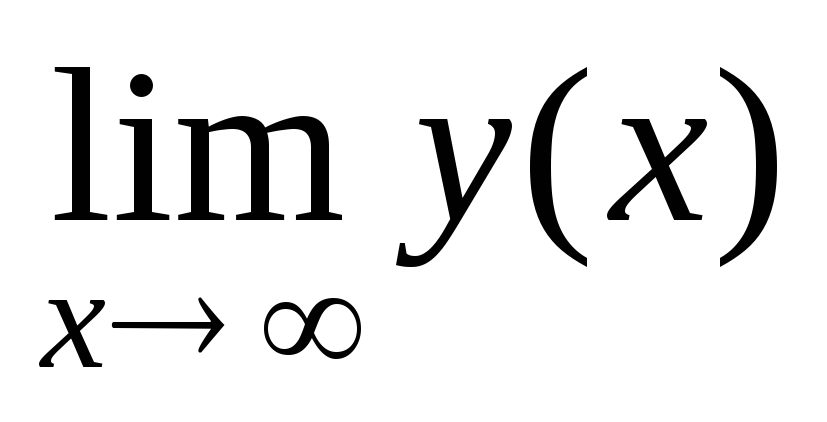 = 0,где
один из символов + ∞, или – ∞.
= 0,где
один из символов + ∞, или – ∞.
Бесконечно малые одного порядка в окрестности точки х0 – бесконечно малые у1(х) и у2(х), предел отношения которых в точке х = х0 равен конечному числу А ≠ 0; если
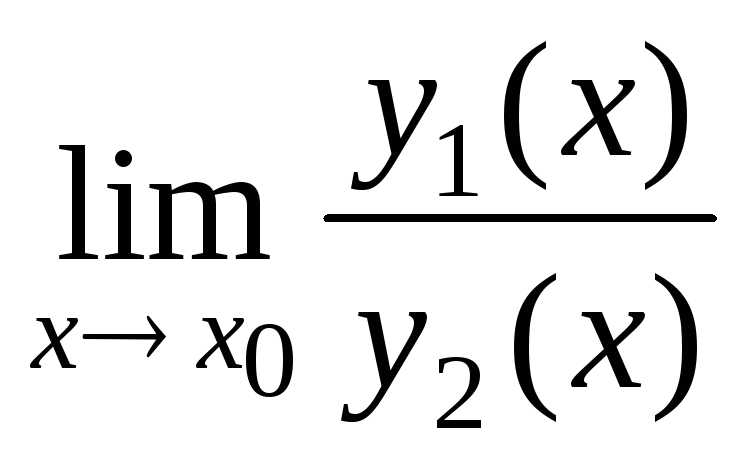 = 0, тоу1(х)
называется бесконечно
малой более высокого порядка,
чем у2(х),
что обозначается как: у1(х)
= ο(у2(х)).
= 0, тоу1(х)
называется бесконечно
малой более высокого порядка,
чем у2(х),
что обозначается как: у1(х)
= ο(у2(х)).
Эквивалентные бесконечно малые в окрестности точки х = х0 – бесконечно малые у1(х) и у2(х), предел отношения которых в точке х = х0 равен 1 (обозначение эквивалентных малых: у1(х) ~ у2(х)). Примеры эквивалентных малых в окрестности точки х = 0: sin α(х) ~ tg α(х) ~ arcsin α(х) ~ arctg α(х) ~ eα(х) – 1 ~ α(х); a α(х) – 1 ~ α(х)·ln a; ln(1 ± α(х)) ~ ± α(х); loga(1 ± α(х)) ~
 ;
(1 ±
α(х))a
– 1
~ ±
a·α(х);
1 –
cos
α(х)
~
;
(1 ±
α(х))a
– 1
~ ±
a·α(х);
1 –
cos
α(х)
~
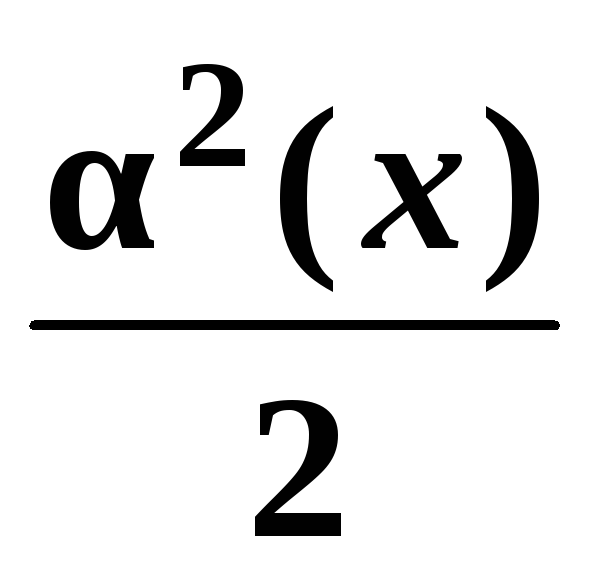 .
.
Таблица некоторых пределов функций:
|
№№ п/п |
Пределы |
Примечания |
|
1. |
|
1-й замечательный предел |
|
2. |
|
2-й замечательный предел, е 2,7183 |
|
3. |
|
|
|
4. |
|
0 < a < + , a ≠ 1 |
|
5. |
|
0 < a < + , a ≠ 1 |
|
6. |
|
a ≠ 0 |
|
7. |
|
– ∞ < a < + ∞ |
|
8. |
|
– ∞ < a < + ∞; неопределенность типа ∞0 при 0 < a < + и типа 00 при – < а < 0 |
|
9. |
|
0 < a < 1; неопределенности нет: 10 = 1 |
|
10. |
|
0 < a < + ; неопределенности нет: С0 = 1 |
|
11. |
|
0 < a < 1 |
|
12. |
|
1 < a < + |
|
13. |
|
0 < a < + |
|
14. |
|
– < а < 0 |
|
15. |
|
0 < a < 1 |
|
16. |
|
1 < a < + |
Методы вычисления предела функции
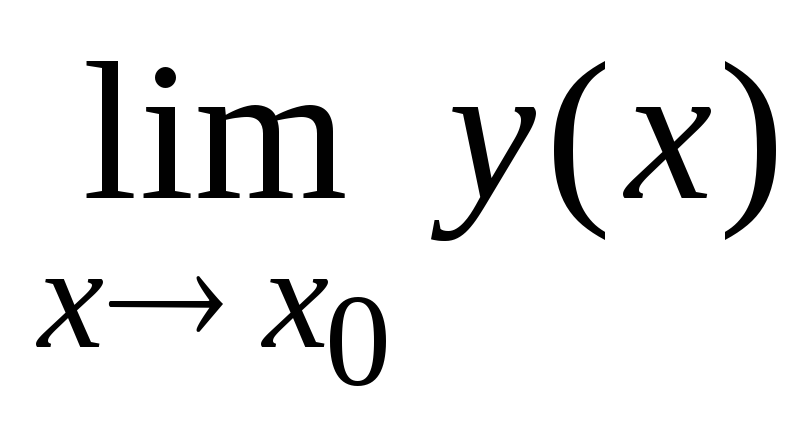 :
:
заменить аргумент функции х его предельным значением х0, используя свойства непрерывных функций:
 = у(х0),
где х0
внутренняя или граничная точка области
определения непрерывной функции у
=
у(х):
если в результате получено конечное
число А
или бесконечное значение предела (+ ∞
или – ∞), то предел найден;
= у(х0),
где х0
внутренняя или граничная точка области
определения непрерывной функции у
=
у(х):
если в результате получено конечное
число А
или бесконечное значение предела (+ ∞
или – ∞), то предел найден;если у(х0) представляет неопределенность, то использовать методы ее раскрытия:
– для
раскрытия неопределенностей вида
![]() и
и
![]() (при этом
(при этом![]() можно свести к
можно свести к![]() ,
т.к. отношение бесконечно больших β1/β2
в силу β1
= 1/α1
и β2
= 1/α2,
где α1
и α2
– бесконечно малые, можно заменить
отношением α2/
α1
= β1/β2):
,
т.к. отношение бесконечно больших β1/β2
в силу β1
= 1/α1
и β2
= 1/α2,
где α1
и α2
– бесконечно малые, можно заменить
отношением α2/
α1
= β1/β2):
а) использовать пределы в приведенной таблице непосредственно или после выполнения определенных тождественных преобразований и замены переменной с целью выделения бесконечно малой; в частности, для некоторых выражений, содержащих тригонометрические функции, указанные операции могут привести к 1-му замечательному пределу;
б) если в числителе и (или) в знаменателе функции у(х) многочлены, то: при х 0 оставить в каждом многочлене член с переменной х в минимальной степени; при х ∞ оставить в каждом многочлене член с переменной х в максимальной степени; при х х0 выделить в каждом многочлене множитель (х – х0), представляющий бесконечно малую величину;
в) в числителе и знаменателе функции использовать эквивалентные бесконечно малые;
г) если бесконечно малой является разность, содержащая корни, то следует эту разность умножить и разделить на такое выражение, которое с учетом формул сокращенного умножения позволит вывести бесконечную малую из иррациональности;
для раскрытия неопределенностей вида (0·∞) и (∞ – ∞) можно, если удастся, непосредственно выполнить операции умножения и вычитания, или сначала преобразовать неопределенности к виду
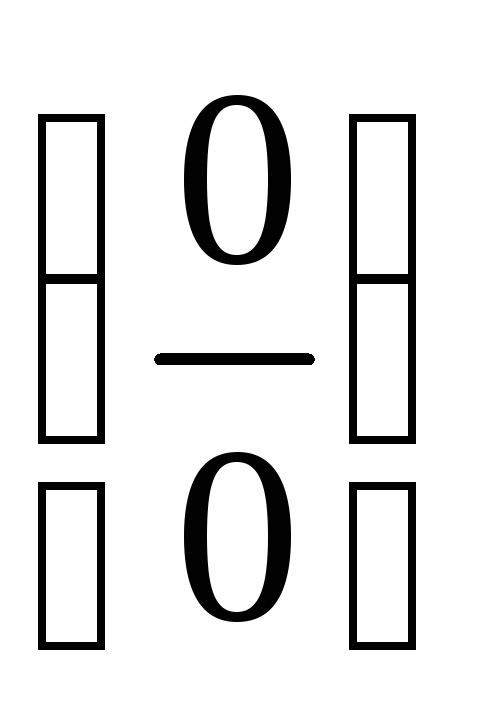 или
или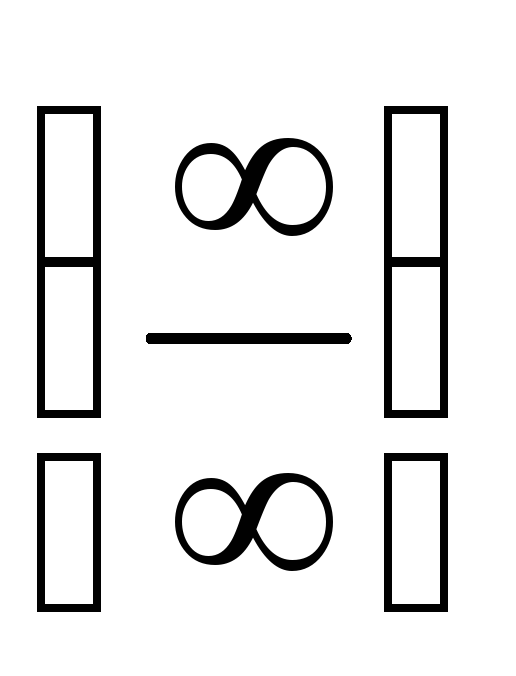 ,
а затем использовать приемыа)
– г);
,
а затем использовать приемыа)
– г);для раскрытия неопределенности вида (1∞) нужно использовать 2-й замечательный предел (см. таблицу пределов) или формулу, получаемую как следствие этого предела:
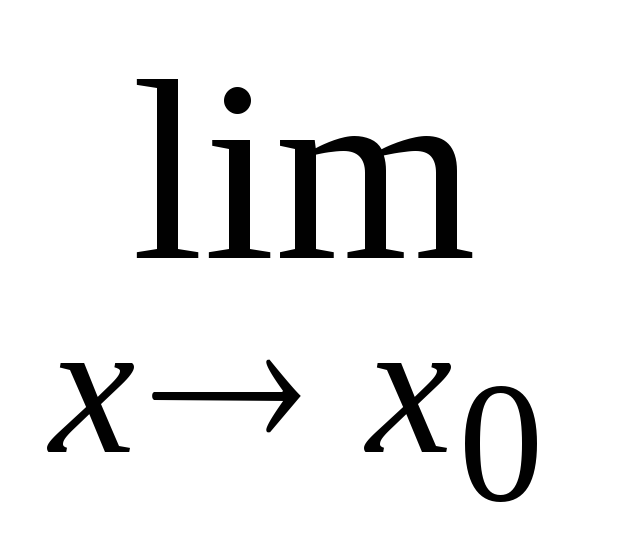 у(х)
=
у(х)
=
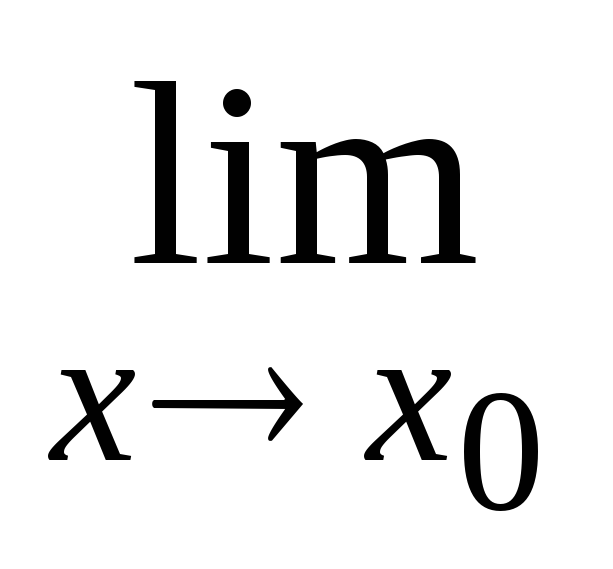 u(x)β(x)
= (1∞)
= exp[
u(x)β(x)
= (1∞)
= exp[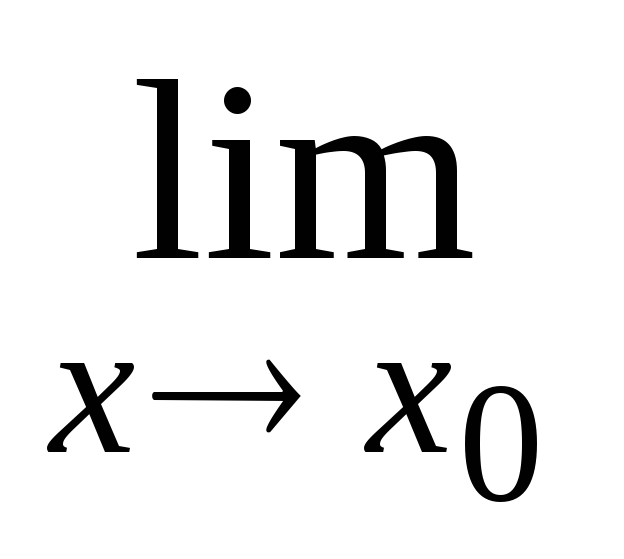 (β(x)·(u(x)
– 1))];
(β(x)·(u(x)
– 1))];для раскрытия неопределенности вида (00) и (∞0) рекомендуется предварительно вычислить предел натурального логарифма функции
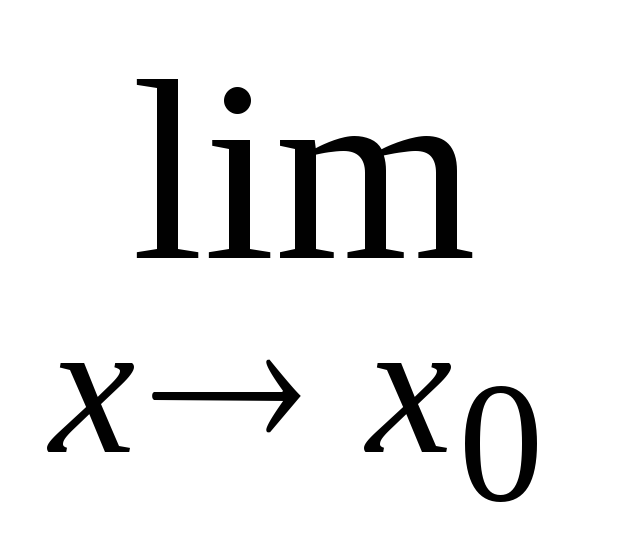 ln
у(х)
= A,
а затем воспользоваться равенством
ln
у(х)
= A,
а затем воспользоваться равенством
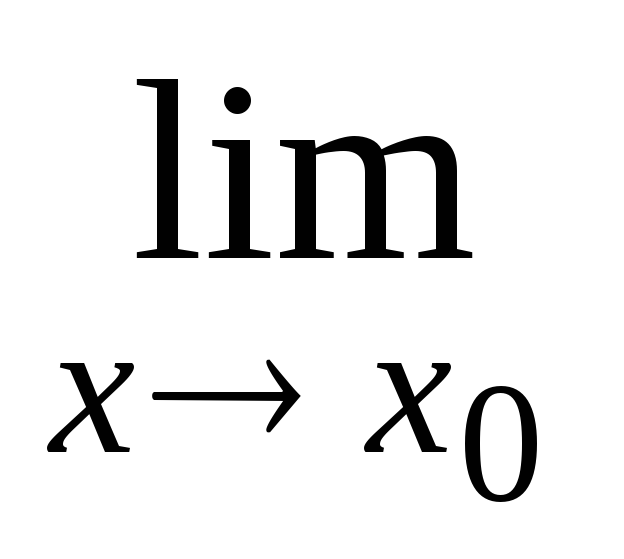 у(х)
=
у(х)
=
 e
ln
y(x)
=
e
ln
y(x)
=
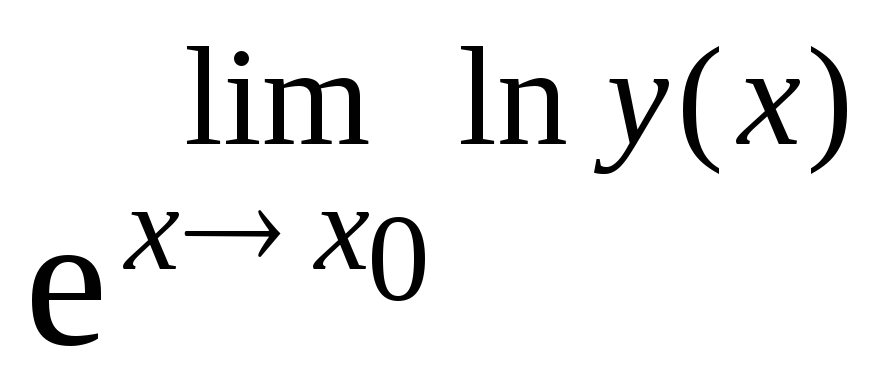 =
е А.
=
е А.
Примечание:
при вычислении
пределов числовых последовательностей
можно воспользоваться равенством:
![]() ,
если заменить п
на
непрерывную переменную х,
а функцию un
= u(n)
на у(х).
,
если заменить п
на
непрерывную переменную х,
а функцию un
= u(n)
на у(х).
Свойства пределов:
предел постоянной у(х) = С равен этой постоянной:
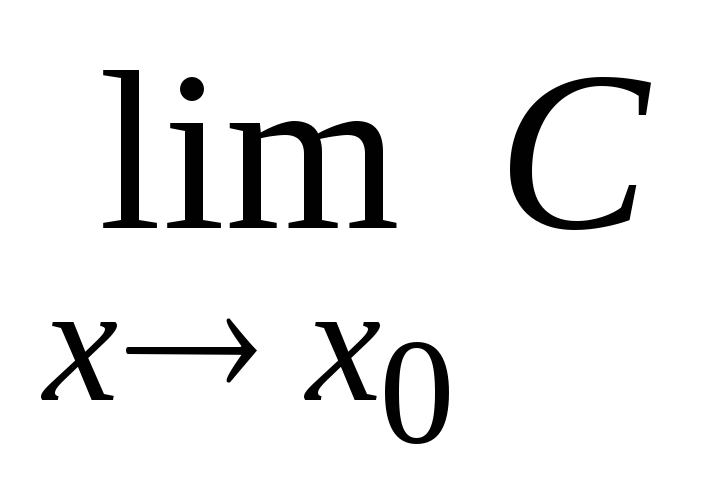 =
С.
=
С.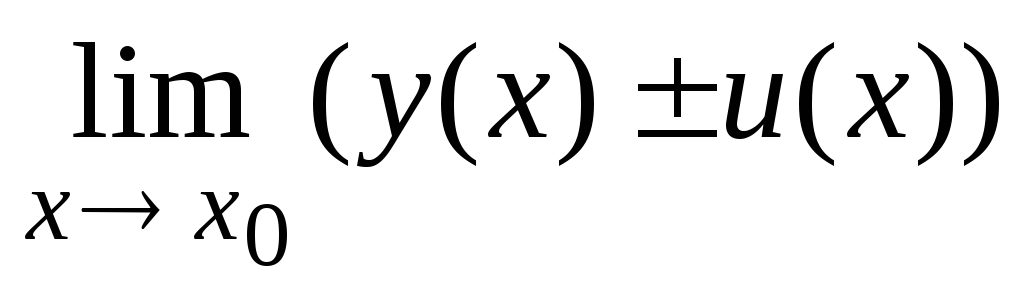 =
=
 ±
±
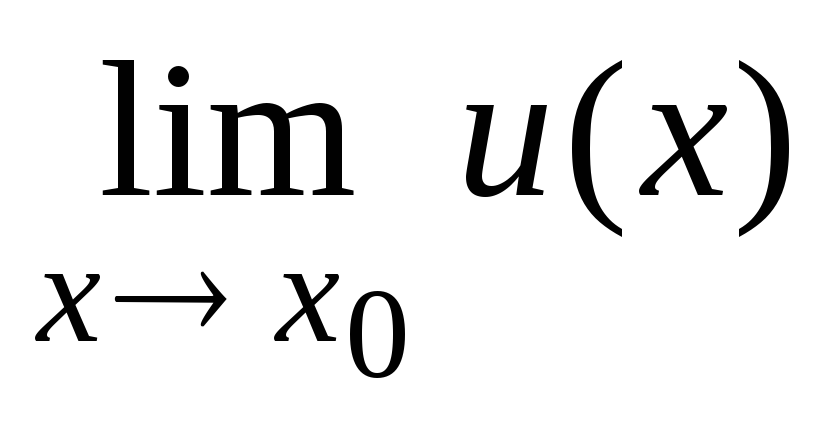 [для непрерывных в точке х0
функций
[для непрерывных в точке х0
функций
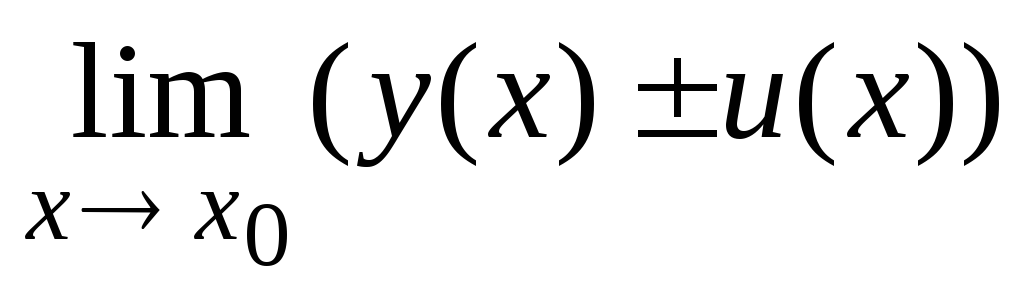 = у(х0)
+ и(х0)];
= у(х0)
+ и(х0)];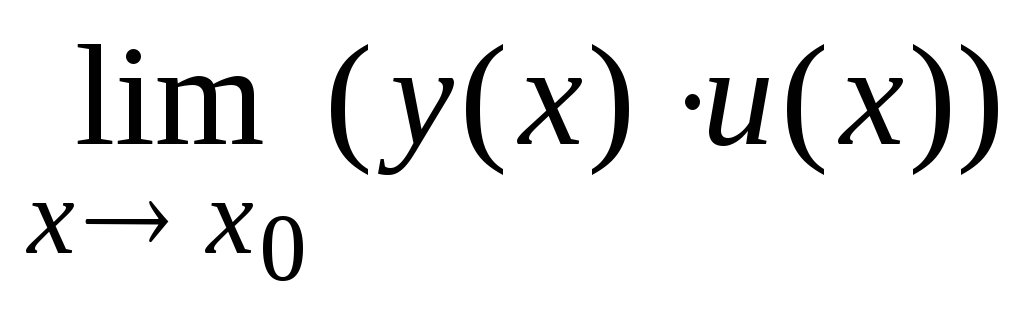 =
=
 ·
·
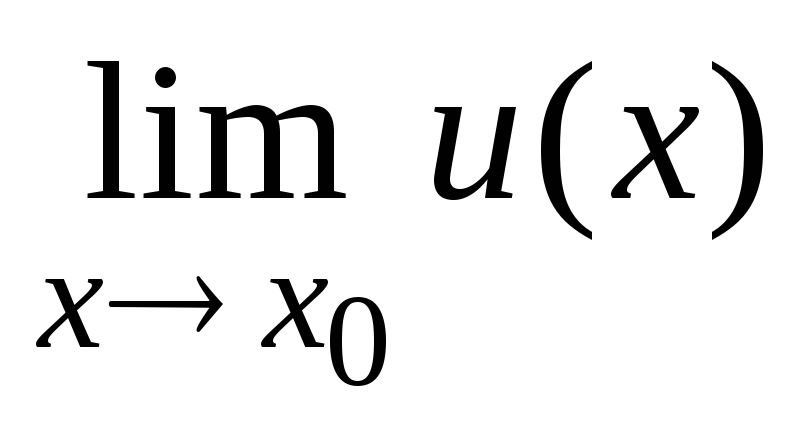 [для
непрерывных в точке х0
функций
[для
непрерывных в точке х0
функций
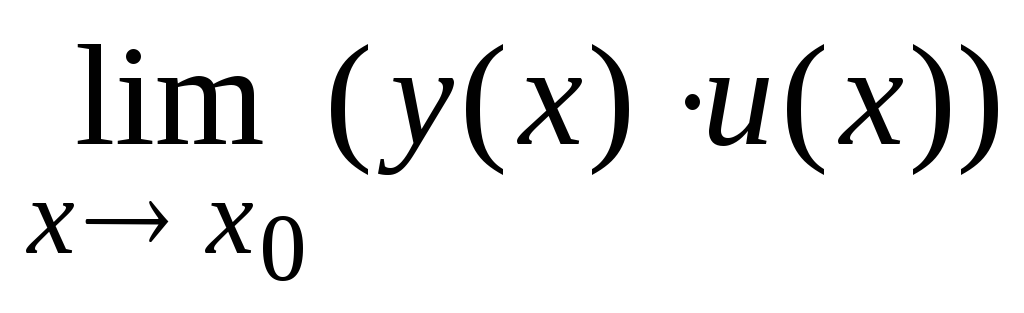 =у(х0)
·
и(х0)];
=у(х0)
·
и(х0)];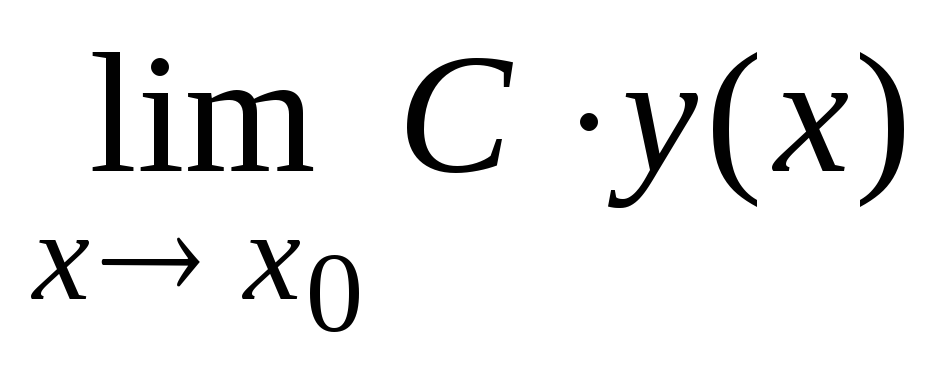 =
=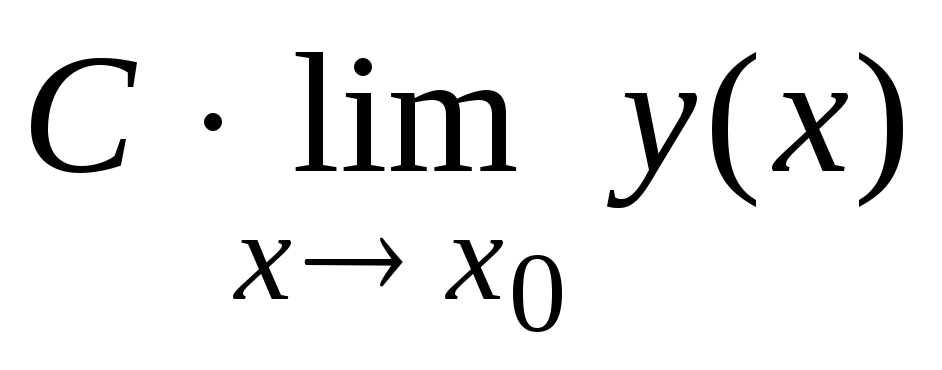 [для
непрерывной
в точке х0
функции
[для
непрерывной
в точке х0
функции
 =C·у(х0)];
=C·у(х0)];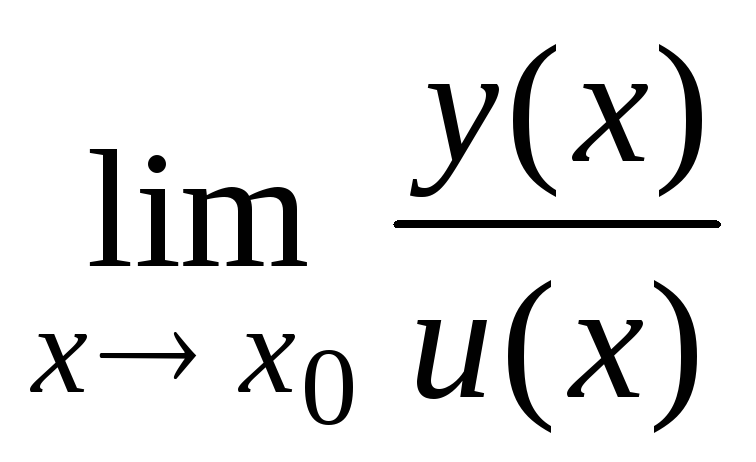 =
= [для
непрерывных
в точке х0
функций
[для
непрерывных
в точке х0
функций
 =
у(х0)/и(х0),
если и(х0)
≠ 0];
=
у(х0)/и(х0),
если и(х0)
≠ 0];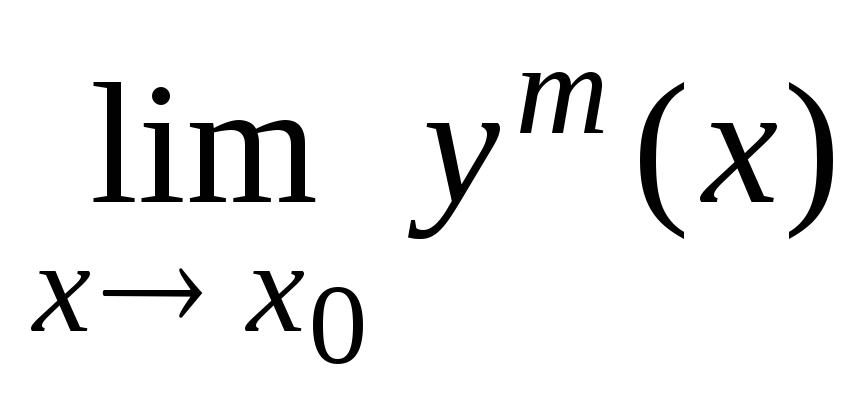 =
(
=
(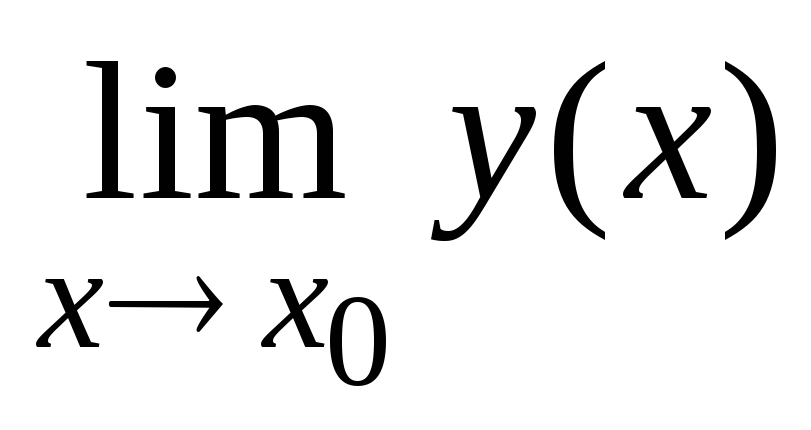 )m
[для
непрерывной в точке х0
функции
)m
[для
непрерывной в точке х0
функции
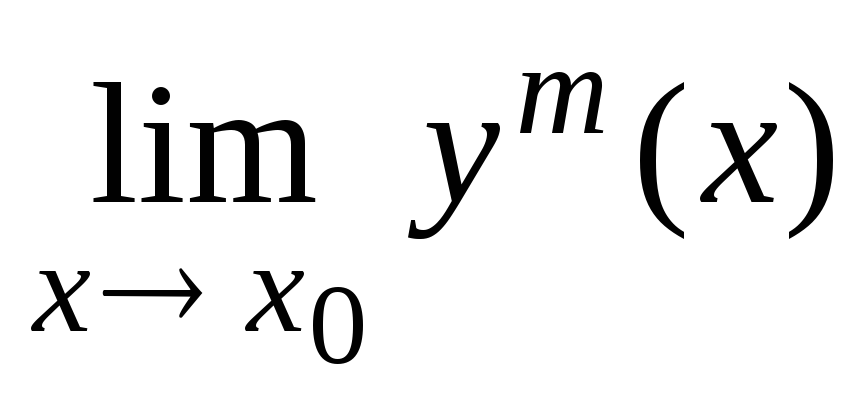 =уm(х0)];
=уm(х0)]; =
=
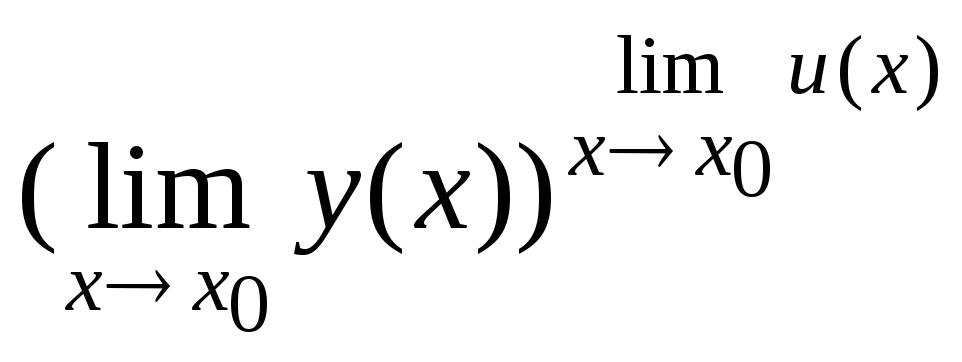 [для непрерывных в точкех0
функций
[для непрерывных в точкех0
функций
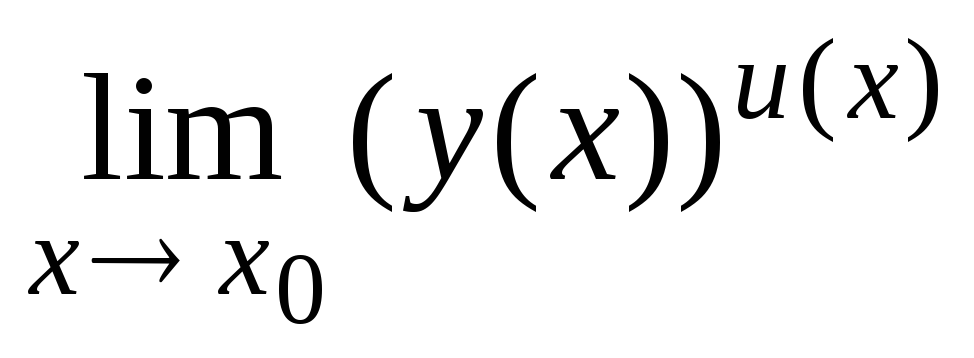 =у(х0)u(x0)].
=у(х0)u(x0)].
Односторонние пределы: предел функции у = у(х), получаемый для любой сходящейся к х0 последовательности {xn} при условии, что все xn < x0, называется пределом слева (обозначение предела слева точки х0:
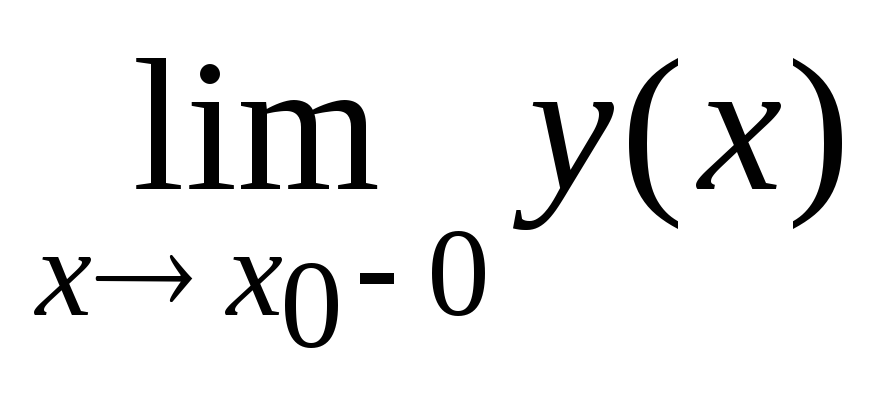 = у(х0
– 0) = А);
предел функции у
= у(х),
получаемый для любой сходящейся к х0
последовательности {xn}
при условии, что все xn
> x0,
называется пределом
справа
(обозначение предела справа точки х0:
= у(х0
– 0) = А);
предел функции у
= у(х),
получаемый для любой сходящейся к х0
последовательности {xn}
при условии, что все xn
> x0,
называется пределом
справа
(обозначение предела справа точки х0:
 = у(х0
+ 0) = В).
= у(х0
+ 0) = В).
Условие непрерывности функции у = у(х) в точке х = х0: у(х0 – 0) = у(х0 + 0) = у(х0).
Точка разрыва 1-го рода – точка х0, в которой правый и левый пределы функции y = y(х) конечны, но не равны друг другу, или, в случае их равенства, сама функция y = y(х) не определена в точке х0 или ее значение в этой точке у(х0) у(х0 – 0) = у(х0 + 0).
Точка разрыва 2-го рода – точка х0, в которой хотя бы один из односторонних пределов функции y = y(х) равен бесконечности (+ или – ) или не существует.
