Справочный материал

к 1-й лабораторной работе

1. Матрица размера m×n – таблица А = (a_ij)_m×n, в которой m строк и n столбцов; a_ij – элемент матрицы, который находится в i-й строке и в j-м столбце (элементом матрицы может быть число, алгебраическое выражение, функция и т.д.).

2. Транспонированная матрица А^Т к матрице А − матрица, строки которой являются соответствующими по номерам столбцами исходной матрицы А; при транспонировании матрицы А размера mn получается матрица А^Т размера nm.

3. Квадратная матрица n-го порядка – матрица, у которой n строк и n столбцов; квадратные матрицы соответственно первого, второго и третьего порядка:

А_11 = (a₁₁); A_22 = 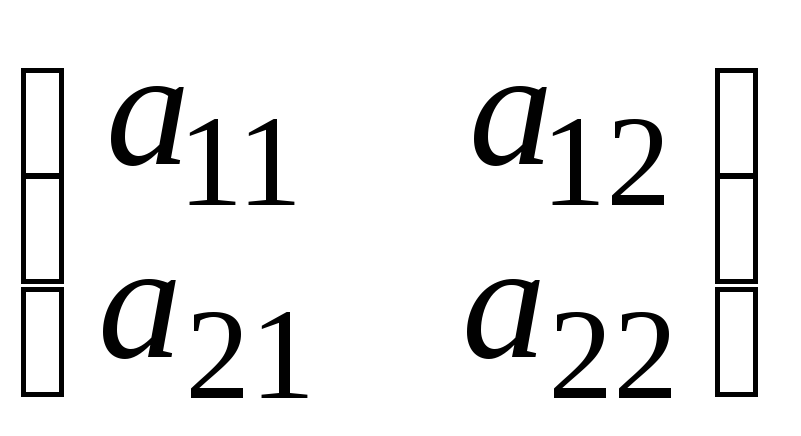; A_33 = .

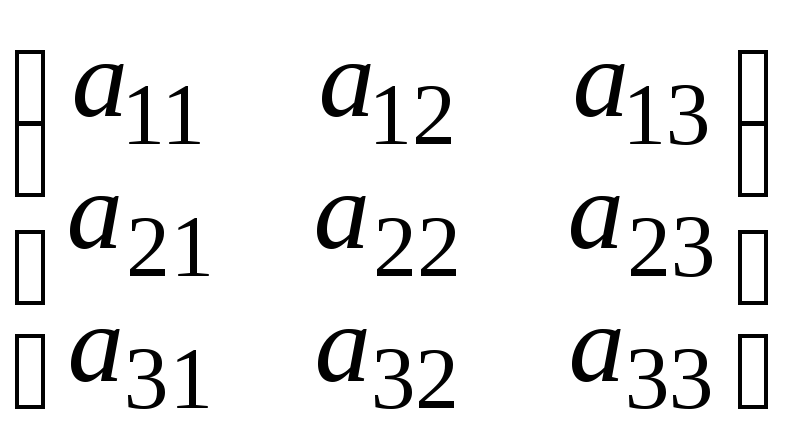4. Главная диагональ квадратной матрицы – диагональ от левого верхнего угла к правому нижнему углу матрицы, т.е. проходящая по элементам матрицы с одинаковыми индексами: a₁₁, a₂₂, …, a_nn; вторая диагональ (от левого нижнего угла к правому верхнему углу) называется побочной диагональю квадратной матрицы.

5. Диагональная матрица – квадратная матрица, все элементы которой, не стоящие на главной диагонали, – нули.

6. Единичная матрица Е – диагональная матрица, все элементы которой на главной диагонали – единицы; Е_n − единичная матрица n-го порядка.

7. Треугольная матрица – квадратная матрица, все элементы которой ниже главной диагонали – нули.

8. Трапецеидальная матрица – матрица, в которой число нулей, стоящих с начала каждой следующей строки, превышает это число нулей в предыдущей строке, все нулевые строки, если они имеются в матрице, расположены ниже последней ненулевой строки, а число столбцов матрицы больше числа ненулевых строк.

9. Матрица ступенчатого вида – треугольная матрица и трапецеидальная матрица.

10. Равенство матриц: две матрицы одинакового размера A = (a_ij)_mn и B = (b_ij)_mn равны, если равны все их соответствующие элементы: a_ij = b_ij; обозначение равенства матриц: A = B.

11. Произведение матриц при умножении матрицы A = (a_ij)_mq слева на матрицу B = (b_ij)_qn – матрица C = (с_ij)_mn = AB, у которой элемент с_ij, стоящий в i-й строке и j-м столбце, равен сумме парных произведений элементов i-й строки матрицы А и соответствующих по номерам элементов j-го столбца матрицы B: с_ij = a_i1∙b_1j + a_i2∙b_2j + …+ a_iq∙b_qj; A(BС) = (АВ)С; A(B + С) = АВ + АС; в общем случае АВ ≠ ВА, однако для квадратной матрицы А n-го порядка: АЕ_n = Е_nА = А.

Внимание! Матрицу А можно умножить слева на матрицу В, если число столбцов матрицы А равно числу строк матрицы В, при этом матрица С = АВ имеет столько строк, сколько строк у матрицы А, и столько столбцов, сколько столбцов у матрицы В.

12. Элементарные преобразования строк и столбцов матрицы:

• взаимная перестановка двух строк или столбцов;

• умножение строки или столбца на произвольное ненулевое число (деление на число а ≠ 0 можно рассматривать как умножение на число 1 ∕ а);

• прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число, или прибавление к элементам одного столбца соответствующих элементов другого столбца, умноженных на одно и то же число (вычитание можно рассматривать как сложение с умноженным на (–1) вторым слагаемым), что кратко формулируется, как: прибавление к одной строке другой строки, умноженной на произвольное число, или прибавление к одному столбцу другого столбца, умноженного на произвольное число.

13. Эквивалентные матрицы – матрицы, которые могут быть получены друг из друга элементарными преобразованиями; обозначение эквивалентных матриц: А ~ В. Элементарными преобразованиями любую ненулевую матрицу можно привести к эквивалентной матрице ступенчатого вида.

14. Определитель (детерминант) квадратной матрицы А_n = (a_ij)_n×n (обозначение определителя: det A или |A|, или Δ) – алгебраическая сумма произведений элементов матрицы, составленных по определенному правилу:

• определитель 1-го порядка det(a₁₁) = a₁₁, т.е. равен самому элементу матрицы;

• определитель 2-го порядка 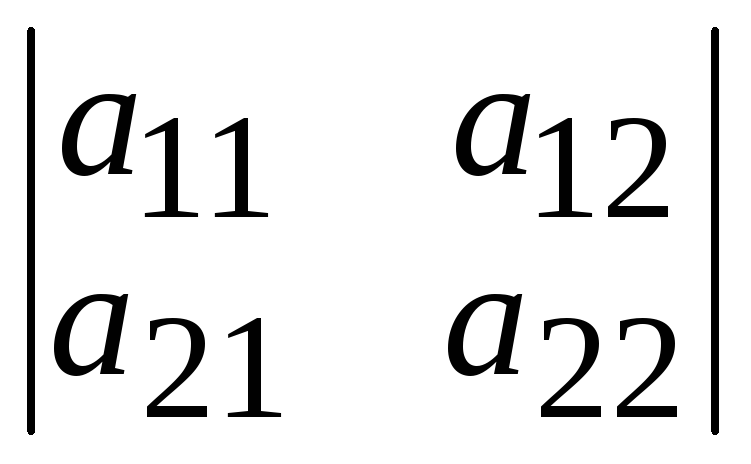= a₁₁∙a₂₂ − a₂₁∙a₁₂, если знак произведения графически заменить отрезком, соединяющим перемножаемые элементы, то схему вычисления определителя 2-го порядка можно представить, как:

• о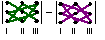пределитель 3-го порядка вычисляется по правилу треугольников, или иначе по правилу Саррюса, т.е. по схеме:

(т.е. определитель 3-го порядка равен сумме произведений из трех множителей, равных элементам на главной диагонали и находящихся в вершинах двух треугольников, одна из сторон которых параллельна главной диагонали, минус сумма произведений из трех множителей, равных элементам на побочной диагонали и находящихся в вершинах двух треугольников, одна из сторон которых параллельна побочной диагонали);

• определитель любого порядка можно вычислять разложением по какой-либо строке или какому-либо столбцу (это приводит к последовательному уменьшению порядка определителя, а определитель до 3-го порядка уже можно рассчитать указанными способами): определитель равен сумме произведений элементов произвольно выбранной строки (произвольно выбранного столбца) на соответствующие им алгебраические дополнения А_ij = (−1)^i+j∙M_ij, где M_ij – минор элемента a_ij, т.е. определитель, получаемый из элементов матрицы после вычеркивания i-й строки и j-го столбца, на пересечении которых стоит этот элемент.