
- •О.Ю. Горлова, в.И. Самарин
- •Лабораторная работа №1 Матрицы и определители
- •Задания
- •Справочный материал
- •12. Элементарные преобразования строк и столбцов матрицы:
- •15. Свойства определителей:
- •17. Матричный метод нахождения обратной матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 2 Системы линейных алгебраических уравнений
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 3 Векторы
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 4 Собственные значения и собственные векторы квадратной матрицы
- •Задание
- •Справочный материал
- •10. Идентификация собственных векторов и собственных значений матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 5 Прямая и плоскость
- •Задания
- •Справочный материал
- •1. Уравнения прямой на плоскости:
- •4. Уравнения плоскости:
- •7. Уравнения прямой в пространстве:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 6 Кривые второго порядка
- •Задания
- •Справочный материал
- •Гипербола
- •Парабола
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 7 Пределы и непрерывность функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 8 Дифференциальное исчисление функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Литература
- •Оглавление
- •Горлова Ольга Юрьевна,
10. Идентификация собственных векторов и собственных значений матрицы:
собственные значения квадратной матрицы А являются действительными корнями уравнения det (А – λE) = 0, где E – единичная матрица, порядок которой совпадает с порядком матрицы А;
координаты собственного вектора р, относящегося к собственному значению λ, находятся из матричного уравнения (А – λE)р = 0, в котором р – вектор-столбец соответствующих координат собственного вектора матрицы А;
собственный вектор матрицы, относящийся к собственному значению λ, определяется с точностью до произвольного числового коэффициента;
собственные векторы, относящиеся к различным собственным значениям, линейно независимы;
симметрическая матрица порядка п всегда имеет п действительных собственных значений с учетом их кратности;
собственные векторы симметрической матрицы, относящиеся к различным собственным значениям, ортогональны между собой;
линейная комбинация собственных векторов матрицы А, относящихся к кратному собственному значению λ, также является собственным вектором этой матрицы, поэтому такими линейными комбинациями исчерпываются все собственные векторы матрицы А, относящиеся к собственному значению λ.
Примеры выполнения заданий лабораторной работы
1.
Найти собственные числа и собственные
векторы матрицы А
=
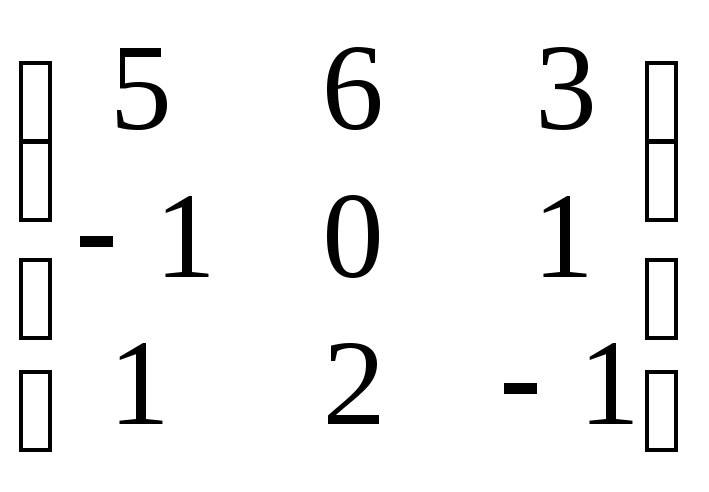 .
.
Решение.
Запишем
уравнение det
(А
– λE)
= 0, корни которого являются собственными
значениями матрицы А:
|А
– λE|
=
 = 0, или вычисляя определитель по правилу
треугольников: (5 –)(–
)(–
1 – )
– 6 + 6 + 3
– 2(5
– )
+ 6(–
1 – )
= 0. Откуда получаем уравнение 3-й степени
относительно :
3
–42
– 4
+ 16 = 0, или 2(
– 4) – 4(
– 4) = 0, или (
– 4)(2
– 4) = 0, или (
– 4)(
– 2)(
+ 2) = 0. Следовательно, имеем три собственных
числа матрицы А:
1
= 4; 2
= 2; 3
= – 2.
= 0, или вычисляя определитель по правилу
треугольников: (5 –)(–
)(–
1 – )
– 6 + 6 + 3
– 2(5
– )
+ 6(–
1 – )
= 0. Откуда получаем уравнение 3-й степени
относительно :
3
–42
– 4
+ 16 = 0, или 2(
– 4) – 4(
– 4) = 0, или (
– 4)(2
– 4) = 0, или (
– 4)(
– 2)(
+ 2) = 0. Следовательно, имеем три собственных
числа матрицы А:
1
= 4; 2
= 2; 3
= – 2.
Собственные
векторы находим из равенства Ар
= р,
которое равносильно матричному уравнению
(А
– λE)р
= 0. Поскольку А
– матрица третьего порядка, то собственный
вектор р
=
![]() .
.
а) Находим собственный вектор для 1 = 4.
Матричное уравнение (А – λ1E)р = 0 принимает вид
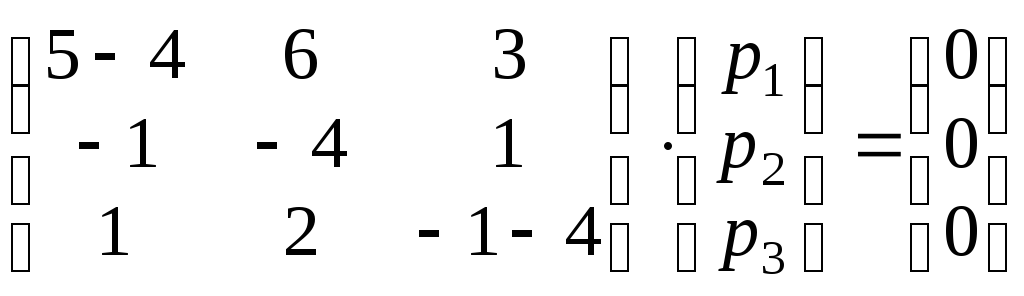 ,
т.е. получаем систему уравнений:
,
т.е. получаем систему уравнений:

Решим полученную систему линейных уравнений методом Гаусса:
стр.:
II+I
стр.:
III–I
стр.:
III+2II
 ~
~
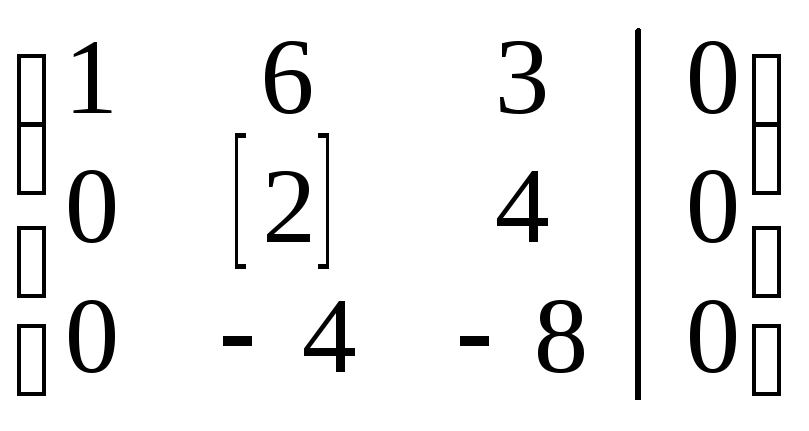 ~
~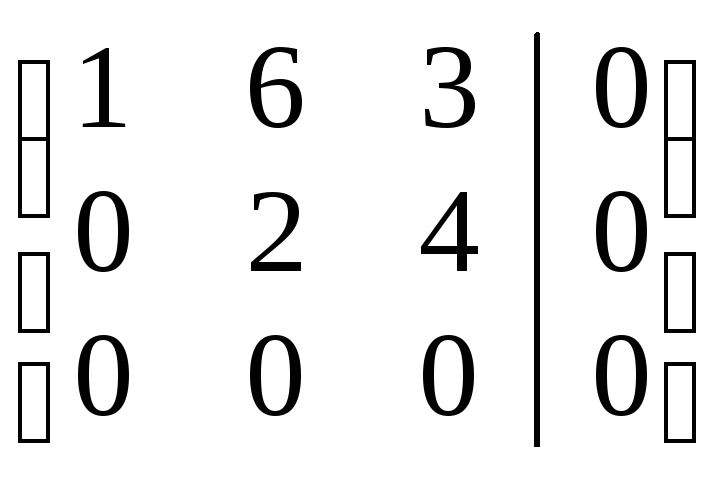 .
.
По
полученной расширенной матрице
ступенчатого вида системы запишем
систему уравнений, равносильную исходной:
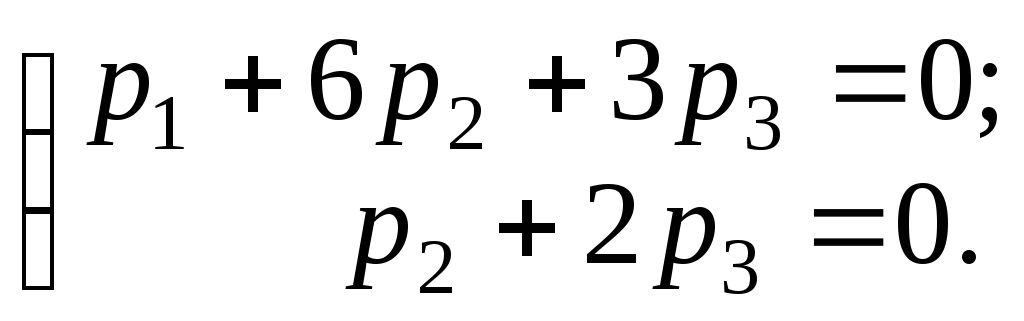
В
полученной системе 2 уравнения и 3
неизвестных, следовательно, в исходной
системе 2 базисных неизвестных и одна
свободная. В качестве базисных неизвестных
возьмем p1
и p2.
Тогда базисные неизвестные находим из
системы:
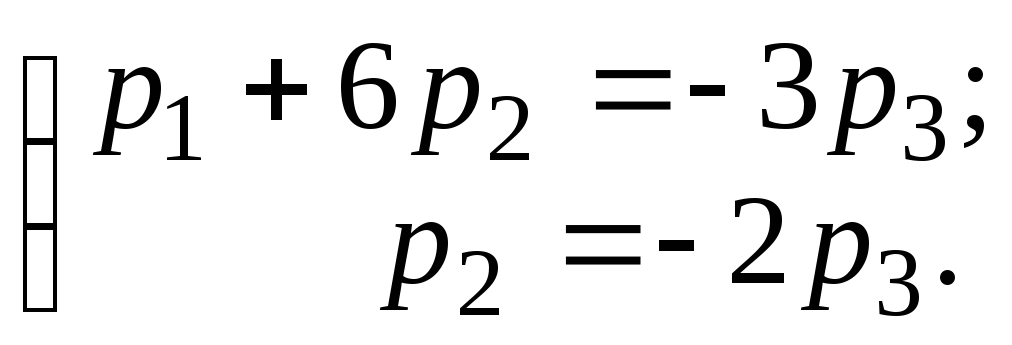
В процессе обратного хода метода Гаусса получаем p2 = – 2р3; р1 = 9р3. Т.о., для 1 = 4 свободный вектор можно записать в следующей координатной форме: р = р3{9; – 2; 1}. Заменяя свободную переменную произвольной константой (р3 = С1), окончательно получим: р = С1{9; – 2; 1}.
б)
Находим
собственный u
=
![]() вектор для 2
= 2.
вектор для 2
= 2.
Матричное уравнение (А – λ2E)u = 0 принимает вид:
 ,
т.е. получаем систему уравнений:
,
т.е. получаем систему уравнений:
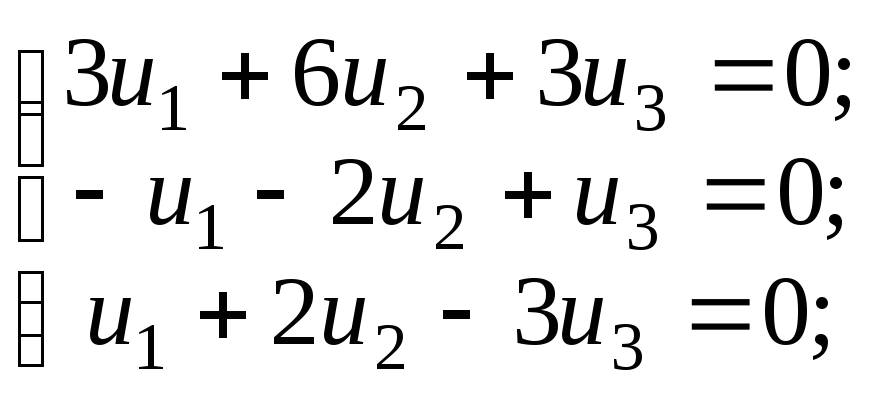 или
или Решая эту систему методом Гаусса,
получаем:
Решая эту систему методом Гаусса,
получаем:
стр.:
II+I
стр.:
III–I
стр.:
III+2II
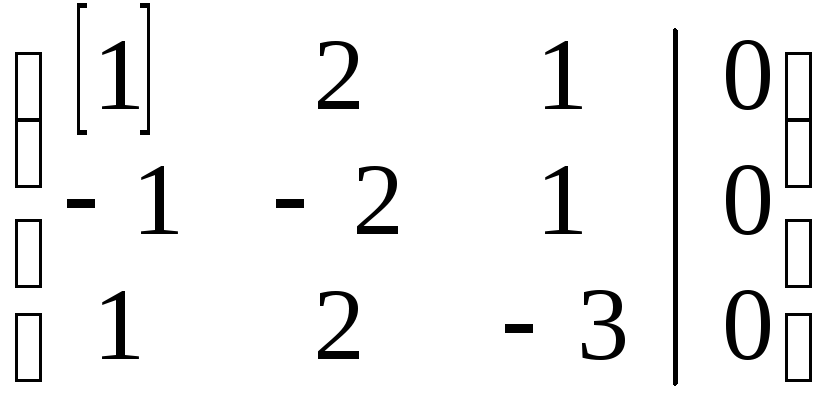 ~
~
 ~
~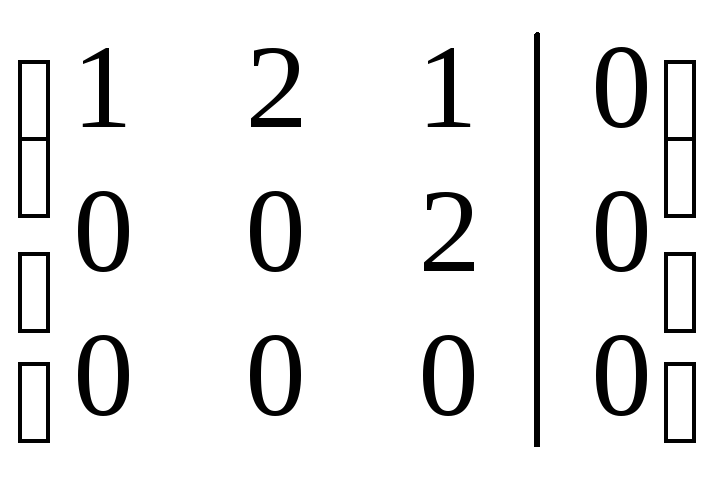 .
.
Т.о.,
исходная система для координат вектора
и
равносильна системе из двух уравнений:
 В качестве базисных неизвестных выбираемu1
и u3,
в качестве свободной – неизвестную u2.
Тогда: u3
= 0; u1
= – 2и2.
Следовательно, для 2
= 2 свободный вектор можно записать в
следующей координатной форме:
и
= и2{–
2; 1; 0}, или как и
= С2{–
2; 1; 0}, где С2
= и2
– произвольная константа.
В качестве базисных неизвестных выбираемu1
и u3,
в качестве свободной – неизвестную u2.
Тогда: u3
= 0; u1
= – 2и2.
Следовательно, для 2
= 2 свободный вектор можно записать в
следующей координатной форме:
и
= и2{–
2; 1; 0}, или как и
= С2{–
2; 1; 0}, где С2
= и2
– произвольная константа.
в)
Находим
собственный v
=
![]() вектор для 3
= – 2.
вектор для 3
= – 2.
Матричное уравнение (А – λ3E)v = 0 принимает вид:
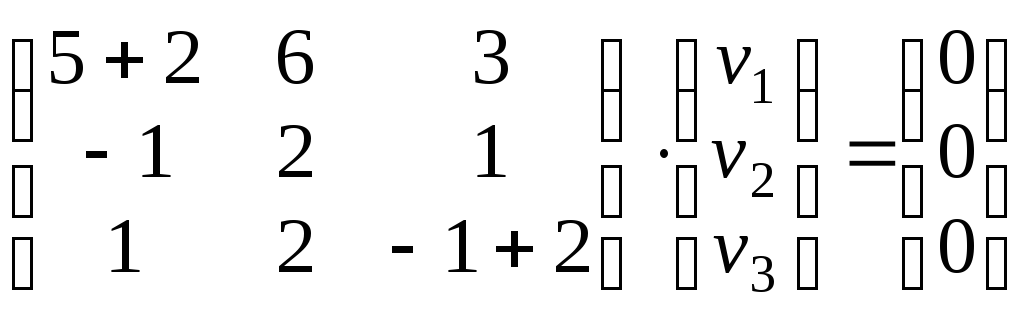 ,
т.е. получаем систему уравнений:
,
т.е. получаем систему уравнений:
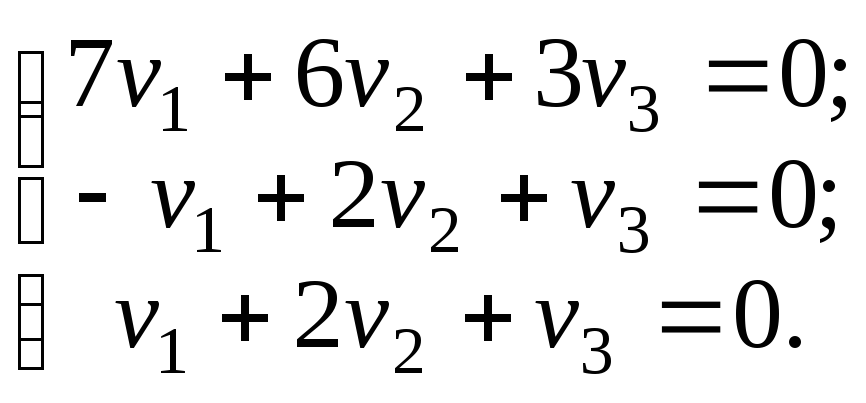 или после перестановки 1-го и 3-го
уравнений:
или после перестановки 1-го и 3-го
уравнений: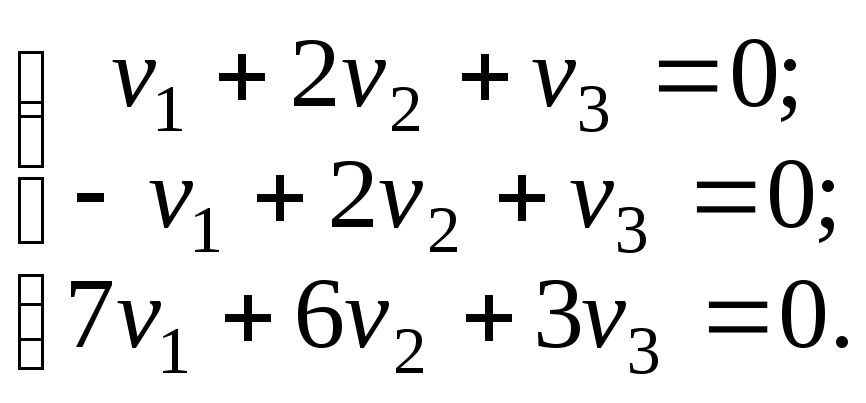 Решая эту систему методом Гаусса,
получаем:
Решая эту систему методом Гаусса,
получаем:
стр.:
II+I
стр.:
III–7I
стр.:
II/2
стр.:
III/4
стр.:
III+II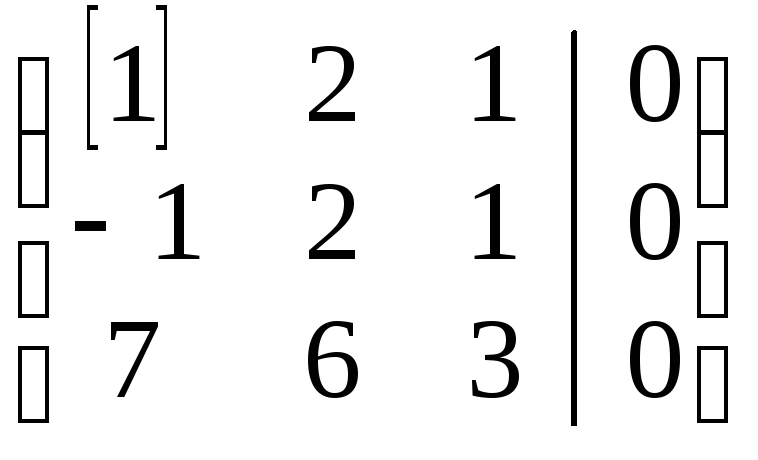
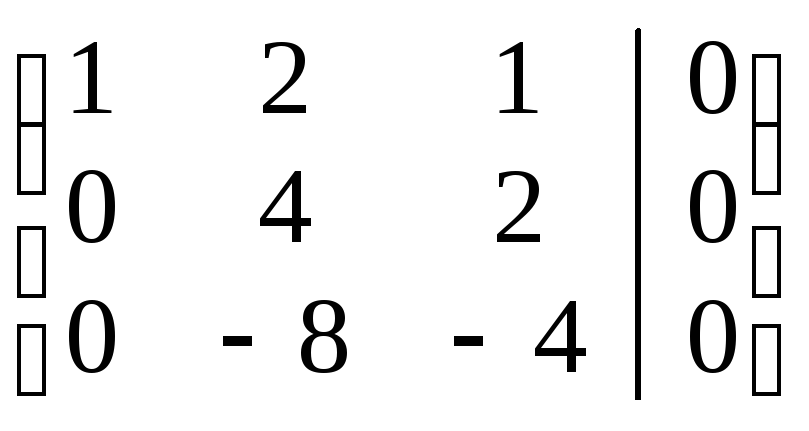 ~
~ ~
~ .
.
Т.о.,
исходная система для координат вектора
v
равносильна системе из двух уравнений:
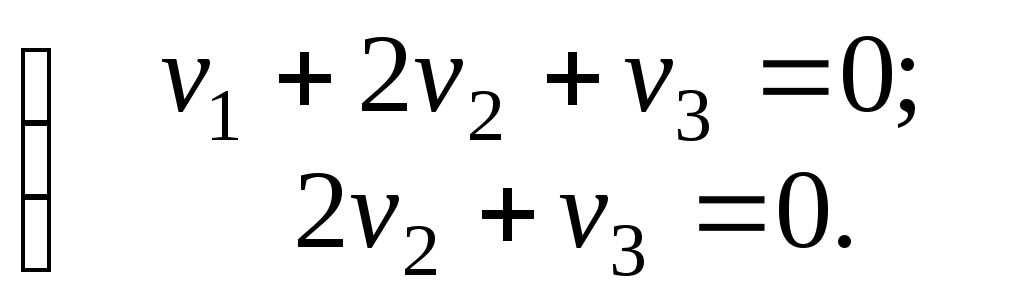 В качестве базисных неизвестных выбираемv1
и v2,
в качестве свободной – неизвестную v3.
Тогда общим решением системы является:
v2
= – v3/2;
v1
= 0. Следовательно, для 3
= – 2 свободный вектор можно записать в
следующей координатной форме: v
= v3{0;
– 1/2; 1}, или v
= С3{0;
– 1; 2}, где произведена замена v3
= 2С3,
С3
– произвольная константа.
В качестве базисных неизвестных выбираемv1
и v2,
в качестве свободной – неизвестную v3.
Тогда общим решением системы является:
v2
= – v3/2;
v1
= 0. Следовательно, для 3
= – 2 свободный вектор можно записать в
следующей координатной форме: v
= v3{0;
– 1/2; 1}, или v
= С3{0;
– 1; 2}, где произведена замена v3
= 2С3,
С3
– произвольная константа.
Ответ: 1 = 4, р = С1{9; – 2; 1};
2 = 2, и = С2{– 2; 1; 0};
3 = – 2, v = С3{0; – 1; 2}.
2.
Найти собственные числа и собственные
векторы матрицы А
=
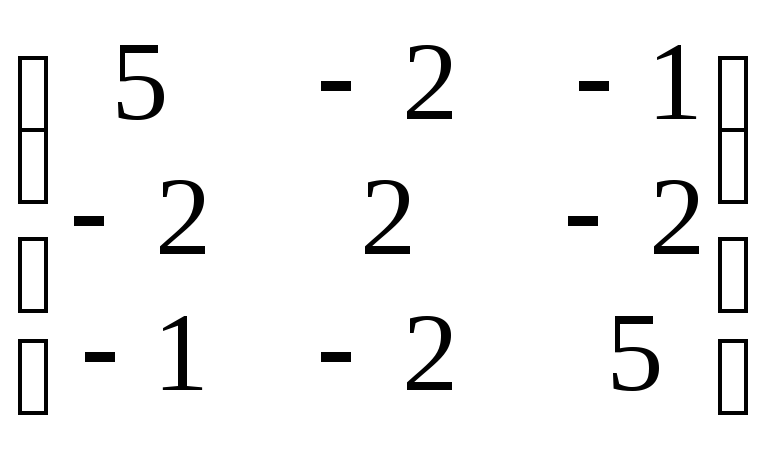 .
.
Решение.
Находим
собственные значения матрицы А:
 = 0, или: (5 –)(2
– )(5
– )
– 4 – 4 – (2 – )
– 4(5
– )
– 4(5
– )
= 0.
= 0, или: (5 –)(2
– )(5
– )
– 4 – 4 – (2 – )
– 4(5
– )
– 4(5
– )
= 0.
Откуда: 3 –122 + 36 = 0, или ( – 6)2 = 0. Следовательно, имеем три собственных числа матрицы А: 1 = 0; 2 = 3 = 6.
а)
Находим собственный вектор р
=
![]() для
1
= 0, которому соответствует матричное
уравнение:
для
1
= 0, которому соответствует матричное
уравнение:
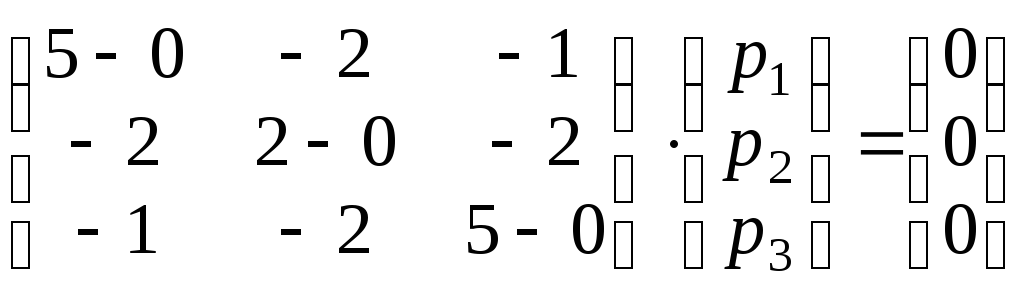 ,
равносильное системе:
,
равносильное системе: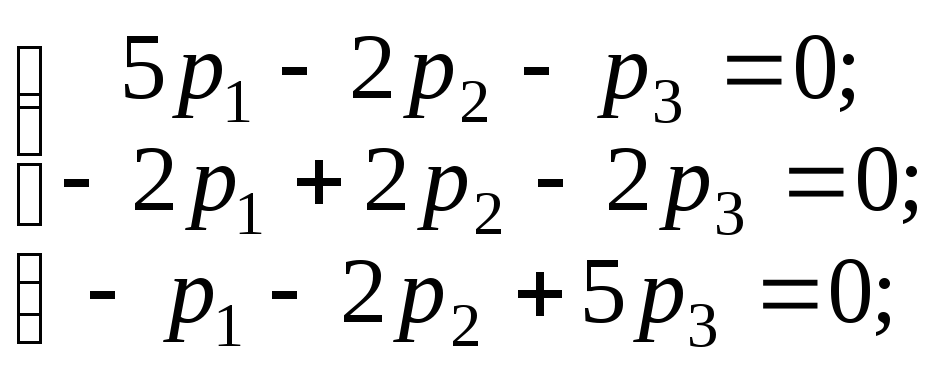 или после перестановки 1-го и 3-го
уравнений:
или после перестановки 1-го и 3-го
уравнений: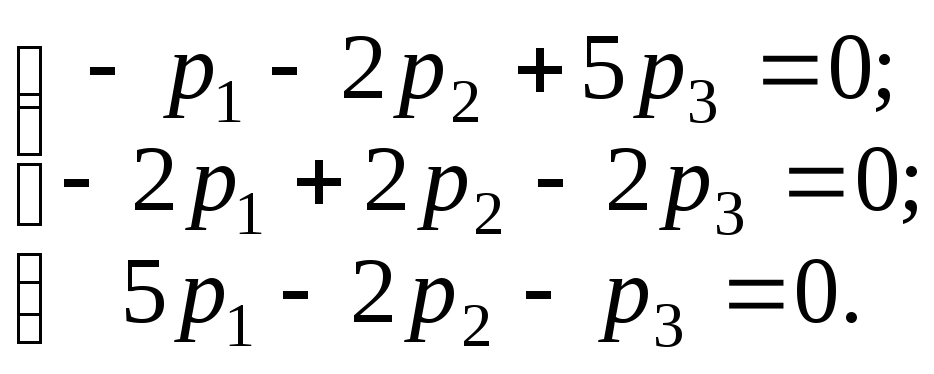 Решаем эту систему методом Гаусса:
Решаем эту систему методом Гаусса:
стр.:
II/6
стр.:
III/12
стр.:
II–2I
стр.:
III+5I
стр.:
III+II
 ~
~
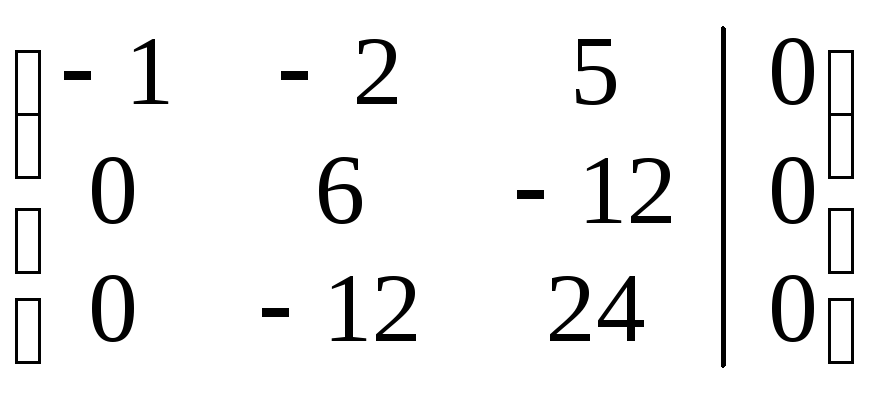 ~
~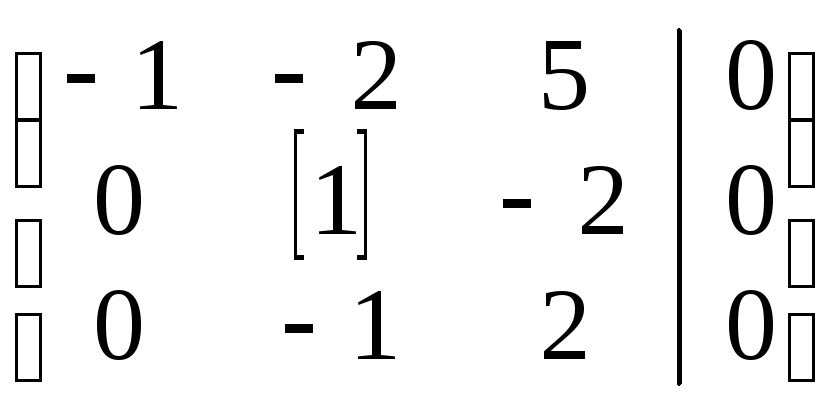 ~
~ .
.
Т.о.,
исходная система для координат вектора
p
равносильна системе из двух уравнений:
 В качестве базисных неизвестных выбираемp1
и p2,
в качестве свободной – неизвестную p3.
Тогда общим решением системы является:
p2
= 2p3;
p1
= p3.
Следовательно, для 1
= 0 свободный вектор можно записать в
следующей координатной форме: p
= p3{1;
2; 1}, или p
= С1{1;
2; 1}, где произведена замена p3
= С1,
С1
– произвольная константа.
В качестве базисных неизвестных выбираемp1
и p2,
в качестве свободной – неизвестную p3.
Тогда общим решением системы является:
p2
= 2p3;
p1
= p3.
Следовательно, для 1
= 0 свободный вектор можно записать в
следующей координатной форме: p
= p3{1;
2; 1}, или p
= С1{1;
2; 1}, где произведена замена p3
= С1,
С1
– произвольная константа.
б)
Находим
собственный вектор u
=
![]() для 2
= 3
= 6, которому соответствует матричное
уравнение:
для 2
= 3
= 6, которому соответствует матричное
уравнение:
 ,
равносильное системе:
,
равносильное системе: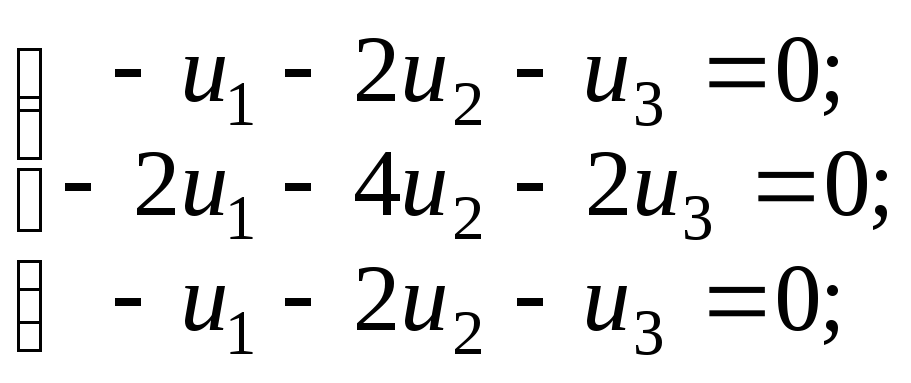 или
или Решаем эту систему методом Гаусса:
Решаем эту систему методом Гаусса:
стр.:
II–2I
стр.:
III–I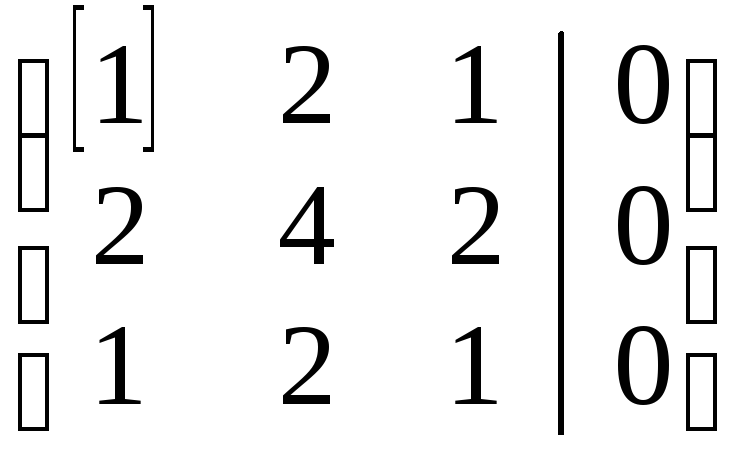
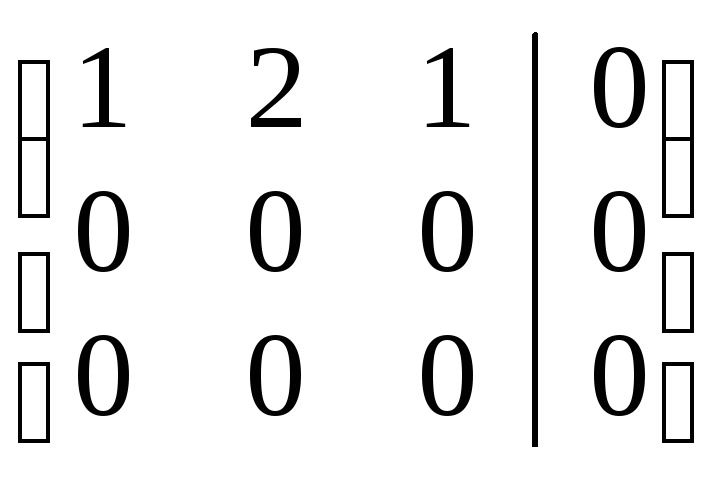 .
.
Т.о., исходная система для координат вектора и равносильна одному уравнению: u1 + 2u2 + u3 = 0, содержащему две свободные неизвестные. В качестве базисной неизвестной выбираем u1, тогда u2 и u3 – свободные неизвестные. Тогда: u1 = – 2и2 – u3. Следовательно, для 2 = 3 = 6 свободный вектор можно записать в следующей координатной форме: и = {– 2u2 – u3; u2; u3}, или, произведя замену свободных неизвестных на произвольные константы (u2 = С2, u3 = С3) как и = {– 2С2 – С3; С2; С3}, или как линейную комбинацию двух собственных векторов: и = {– 2С2; С2; 0} + {– С3; 0; С3} = С2{–2; 1; 0} + C3{–1; 0; 1}.
Ответ: 1 = 0, р = С1{1; 2; 1};
2 = 3 = 6, и = С2{–2; 1; 0} + C3{–1; 0; 1}.
3.
Найти собственные числа и собственные
векторы матрицы А
=
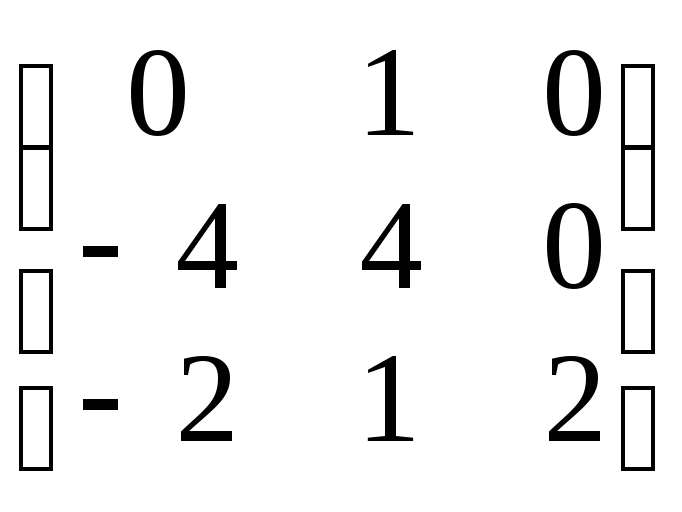 .
.
Решение.
Находим
собственные значения матрицы А:
 = 0, или: –(4
– )(2
– )
+ 4(2
– )
= 0, откуда: 3
–62
+ 12
– 8 = (
– 2)3
= 0. Следовательно, имеем три равных друг
другу собственных числа матрицы А:
1
= 2
= 3
= 2.
= 0, или: –(4
– )(2
– )
+ 4(2
– )
= 0, откуда: 3
–62
+ 12
– 8 = (
– 2)3
= 0. Следовательно, имеем три равных друг
другу собственных числа матрицы А:
1
= 2
= 3
= 2.
Находим
собственный вектор р
=
![]() для 1
= 2
= 3
= 2, которому соответствует матричное
уравнение:
для 1
= 2
= 3
= 2, которому соответствует матричное
уравнение:
 ,
равносильное системе:
,
равносильное системе: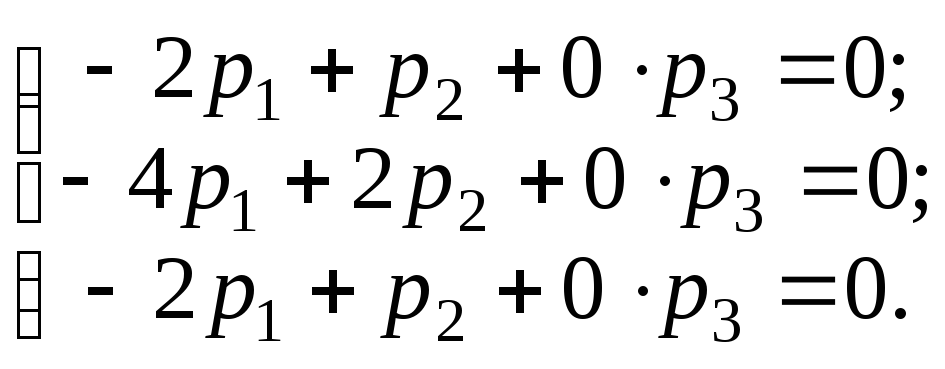 Решаем эту систему методом Гаусса:
Решаем эту систему методом Гаусса:
стр.:
II–2I
стр.:
III–I
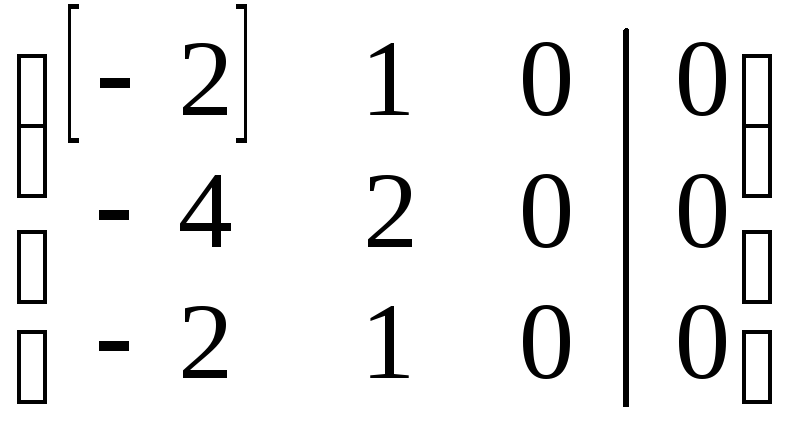 ~
~
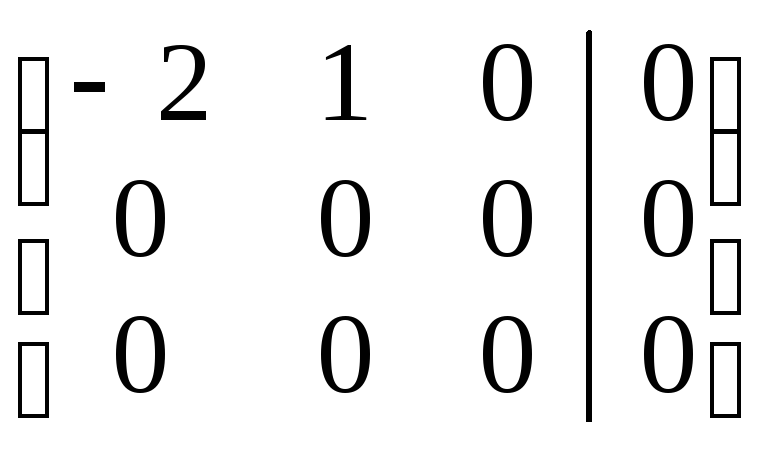 .
.
Т.о., исходная система для координат вектора р равносильна одному уравнению: – 2р1 + р2 + 0р3 = 0, содержащему две свободные неизвестные. Ясно, что р3 – произвольное число, пусть второй свободной неизвестной будет р2. Тогда р1 – базисная неизвестная, и р1 = р2/2 – 0р3. Следовательно, для 1 = 2 = 3 = 2 свободный вектор можно записать в следующей координатной форме: р = {р2/2; р2; р3}, или, произведя замену свободных неизвестных на произвольные константы (р2 = 2С1, р3 = С2) как р = {С1; 2С1; С2}, или как линейную комбинацию двух собственных векторов: р = {С1; 2С1; 0} + {0; 0; С2} = С1{1; 2; 0} + C2{0; 0; 1}.
Ответ: 1 = 2 = 3 = 2, р = С1{1; 2; 0} + C2{0; 0; 1}.
