
- •О.Ю. Горлова, в.И. Самарин
- •Лабораторная работа №1 Матрицы и определители
- •Задания
- •Справочный материал
- •12. Элементарные преобразования строк и столбцов матрицы:
- •15. Свойства определителей:
- •17. Матричный метод нахождения обратной матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 2 Системы линейных алгебраических уравнений
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 3 Векторы
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 4 Собственные значения и собственные векторы квадратной матрицы
- •Задание
- •Справочный материал
- •10. Идентификация собственных векторов и собственных значений матрицы:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 5 Прямая и плоскость
- •Задания
- •Справочный материал
- •1. Уравнения прямой на плоскости:
- •4. Уравнения плоскости:
- •7. Уравнения прямой в пространстве:
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 6 Кривые второго порядка
- •Задания
- •Справочный материал
- •Гипербола
- •Парабола
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 7 Пределы и непрерывность функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Лабораторная работа № 8 Дифференциальное исчисление функций одной переменной
- •Задания
- •Справочный материал
- •Примеры выполнения заданий лабораторной работы
- •Литература
- •Оглавление
- •Горлова Ольга Юрьевна,

Гипербола
Парабола

Эксцентриситет ε кривой второго порядка (кроме окружности) – отношение расстояния r от точки M до фокуса кривой второго порядка к расстоянию d от точки M до соответствующей этому фокусу директрисы, т.е. эксцентриситет ε = r/d. Для эллипса ε = r/d = c/a < 1; для гиперболы ε = r/d = c/a > 1; для параболы ε = r/d = 1; у окружности эксцентриситет равен 0.
Уравнения директрис кривых второго порядка: уравнения директрис эллипса и гиперболы: х = ± а/ = ± а2/с, где; уравнение директрисы параболы x = − p/ 2.
Если алгебраическое уравнение А∙x2 + В∙x∙y + С∙y2 + D∙x + E∙y + F = 0 задает кривую второго порядка, то тип этой кривой определяется значением определителя =
 :
при
> 0 кривая
2-го порядка – эллипс (в случае А
= С
и В
= 0 – окружность),
при δ < 0
– гипербола, при δ
= 0 – парабола.
:
при
> 0 кривая
2-го порядка – эллипс (в случае А
= С
и В
= 0 – окружность),
при δ < 0
– гипербола, при δ
= 0 – парабола.
Главные оси кривой второго порядка – координатные оси правой прямоугольной системы координат, в которой уравнение этой кривой является каноническим.
Примеры выполнения заданий лабораторной работы
1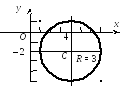 .
Указать тип кривой и построить эту
кривую по ее уравнению: а)
(х
– 4)2
+
(у
+ 2)2
= 9;
б)
.
Указать тип кривой и построить эту
кривую по ее уравнению: а)
(х
– 4)2
+
(у
+ 2)2
= 9;
б)
![]() ;в)
;в)
![]() ;г)
у2
= – 2,5х.
;г)
у2
= – 2,5х.
Решение.
а) Кривая, задаваемая уравнением
(х – 4)2 + (у + 2)2 = 9, – окружность ра-
диуса R = 3 и центром в точке С(4; –2):
б) Кривая, задаваемая уравнением
![]()
 ,
– эллипс, большая ось которого 2а
= 2
,
– эллипс, большая ось которого 2а
= 2![]() = 12 находится на осиОх,
меньшая ось, равная 2b
= 2
= 12 находится на осиОх,
меньшая ось, равная 2b
= 2![]() = 8, находится на осиОу.
Эллипс, задаваемый уравнением
= 8, находится на осиОу.
Эллипс, задаваемый уравнением
![]() ,
– центрально симметричная
,
– центрально симметричная
кривая относительно начала координат, впи-
с анная
в прямоугольник со сторонами 2а
и 2b,
анная
в прямоугольник со сторонами 2а
и 2b,
параллельными координатным осям Ох и Оу
соответственно:
в )
Кривая, задаваемая уравнением
)
Кривая, задаваемая уравнением
![]() ,
– гипербола, действительная ось которой
2а
= 2
,
– гипербола, действительная ось которой
2а
= 2![]() = 3 находится на осиОу,
а мнимая, равная 2b
= 2
= 3 находится на осиОу,
а мнимая, равная 2b
= 2![]() = 10, находится на осиОх.
Гипербола, задаваемая урав-
= 10, находится на осиОх.
Гипербола, задаваемая урав-
нением
![]() ,
– центрально симметрич-
,
– центрально симметрич-
ная кривая относительно начала координат, вер-
шины
которой касаются сторон п рямоугольника
рямоугольника
со сторонами 2а и 2b, параллельными координат-
ным осям Ох и Оу соответственно, а ветви нахо-
дятся в верхнем и нижнем секторах, образован-
ных диагоналями этого прямоугольника, которые
являются асимптотами этой гиперболы:
г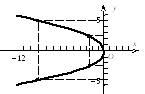 )
Кривая, задаваемая уравнением у2
= – 2,5х,
парабола, ось симметрии которой – ось
Ох,
вершина находится в начале координат,
а ветви расположены слева от оси Оу,
поскольку х
0. Строим заданную параболу по точкам:
)
Кривая, задаваемая уравнением у2
= – 2,5х,
парабола, ось симметрии которой – ось
Ох,
вершина находится в начале координат,
а ветви расположены слева от оси Оу,
поскольку х
0. Строим заданную параболу по точкам:
|
х |
0 |
– 2,5 |
– 10 |
|
у |
0 |
2,5 |
5 |
Указания к выполнению задания 2:
По знаку определителя =
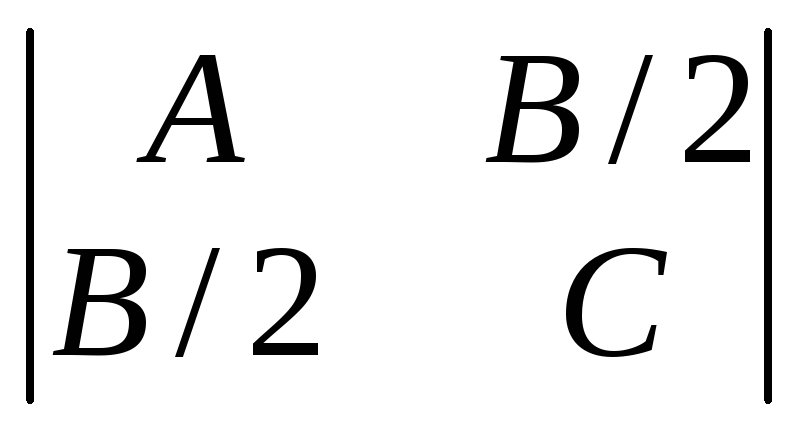 квадратичной формы в уравнении кривой
второго порядкаА∙x2
+
В∙x∙y
+
С∙y2
+
D∙x
+
E∙y
+
F
=
0
(в уравнении задания В
= 0) определить тип этой кривой (эллипс
или гипербола).
квадратичной формы в уравнении кривой
второго порядкаА∙x2
+
В∙x∙y
+
С∙y2
+
D∙x
+
E∙y
+
F
=
0
(в уравнении задания В
= 0) определить тип этой кривой (эллипс
или гипербола).Используя способ Лагранжа, выделить в левой части уравнения полные квадраты (х – х0)2 и (у – у0)2 для соответствующих переменных, входящих в уравнение во второй степени . Определить координаты центра системы координат О(х0; у0), оси которой Оu и Оv направлены вдоль главных осей кривой 2-го порядка и параллельны осям Ох и Оу.
Алгебраическими преобразованиями привести уравнение к каноническому виду соответствующей кривой:
 – для эллипса (а2
> b2),
– для эллипса (а2
> b2),
 – для гиперболы. Записать значенияа,
b
и с:
для эллипса
– для гиперболы. Записать значенияа,
b
и с:
для эллипса
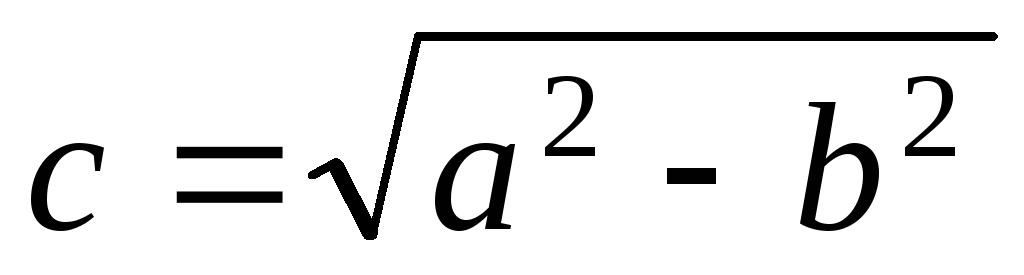 ,
для гиперболы
,
для гиперболы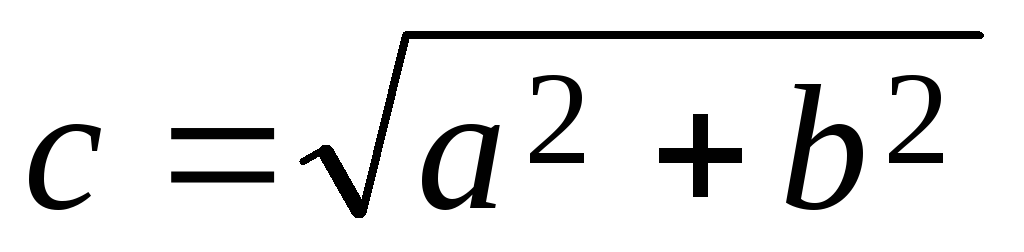 .
.С учетом нового центра координат О(х0; у0) по значениям а и b построить эллипс или гиперболу, задаваемых исходным уравнением.
Определить направления главных осей Оu и Оv кривой 2-го порядка: ось Оu направлена вдоль большей оси эллипса или вдоль действительной оси гиперболы сонаправлено координатной оси Ох или оси Оу, ось Оv перпендикулярна оси Оu и с этой осью образует правую систему координат.
Записать координаты вершин и фокусов кривой, уравнения асимптот (для гиперболы) и директрис, вычислить эксцентриситет кривой.
|
Характеристики кривой |
Произведенная замена переменных |
Эллипс |
Гипербола |
|
Координаты вершин |
Если: х – х0 = u, y – y0 = v, т.е.
если Оu
|
А1(а + х0; у0); А2(– а + х0; у0); В1(x0; b + y0); B2(x0; – b + y0) |
А1(а + х0; у0); А2(– а + х0; у0) |
|
Если: y – y0 = u, х – х0 = –v, т.е.
если Оu
|
А1(х0; а + у0); А2(х0; – а + у0); В1(– b + х0; у0); B2(b + х0; у0) |
А1(х0; а + у0); А2(х0; – а + у0) | |
|
Координаты фокусов |
Если: х – х0 = u, y – y0 = v |
F1(с + х0; у0), F2(– с + х0; у0) | |
|
Если: y – y0 = u, х – х0 = –v |
F1(х0; с + у0), F2(х0; – с + у0) | ||
|
Уравнения директрис |
Если: х – х0 = u, y – y0 = v |
х
=
| |
|
Если: y – y0 = u, х – х0 = –v |
у
=
| ||
|
Уравнения асимптот |
Если: u = х – х0, v = y – y0 |
– |
у
=
|
|
Если: u = y – y0, v = х – х0 |
– |
у
=
| |
2. Определить тип кривой второго порядка по ее общему уравнению; привести это уравнение к главным осям и построить соответствующую кривую; определить координаты вершин и фокусов кривой, записать уравнения асимптот (если они есть) и директрис; вычислить эксцентриситет кривой: а) х2 + 3у2 – 6х – 12у + 15 = 0; б) 4х2 + у2 + 16х – 2у + 8 = 0; в) х2 – у2 + 6х – 2у + 6 = 0; г) 5х2 – 4у2 + 10х + 16у + 9 = 0.
Решение.
а)
В квадратичной форме уравнения кривой
х2
+ 3у2
– 6х
– 12у
+ 15 = 0: А
= 1, В
= 0, С
=
3, то определитель
=
![]() =
=![]() = 3 > 0. Следовательно, кривая, задаваемая
этим уравнением, – эллипс.
= 3 > 0. Следовательно, кривая, задаваемая
этим уравнением, – эллипс.
Выделим
полные квадраты переменных способом
Лагранжа. Для этого в уравнении кривой
группируем неизвестные: (х2
– 6х)
+ (3у2–
12у)
+ 15 = 0. Поскольку х2
– 6х
= (х2
– 6х
+ 9) – 9 = (х
– 3)2
– 9 и 3у2–
12у
= 3(у2
– 4у)
= 3(у2
– 4у
+ 4) – 12 = 3(у
– 2)2
– 12, то уравнение кривой принимает вид:
(х
– 3)2
– 9 + 3(у
– 2)2
– 12 + 15 = 0, или (х
– 3)2
+ 3(у
– 2)2
= 6. После деления полученного уравнения
на 6 получаем:
![]() =
1.
=
1.
Больший
знаменатель полученного уравнения
эллипса является параметром а2,
т.е. а2
= 6 и b2
= 2. Т.о., имеем: а
=
![]() ≈
2,45;
b
=
≈
2,45;
b
=
![]() ≈
1,41;
с
=
≈
1,41;
с
=
![]() =
=![]() =
2.
=
2.
Поскольку
согласно полученному уравнению большая
ось 2а
эллипса параллельна оси Ох,
то ось Оu
![]() Ох
а ось Оv,
образуя с Оu
правую систему координат, сонаправлена
оси Оу,
что соответствует
замене переменных: х
– х0
=
х
– 3 = u,
y
– y0
=
y
– 2 = v.
В координатной системе Оuv
получаем каноническое уравнение эллипса:
Ох
а ось Оv,
образуя с Оu
правую систему координат, сонаправлена
оси Оу,
что соответствует
замене переменных: х
– х0
=
х
– 3 = u,
y
– y0
=
y
– 2 = v.
В координатной системе Оuv
получаем каноническое уравнение эллипса:
![]() =
1,
причем поскольку х0
= 3, у0
= 2, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(3;
2).
=
1,
причем поскольку х0
= 3, у0
= 2, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(3;
2).
Для
построения эллипса чертим в координатной
системе Оuv
прямоугольник
с центром в точке О
и сторонами длиной 2а
= 2![]() ≈ 4,9, параллельными осиОu,
и
длиной 2b
= 2
≈ 4,9, параллельными осиОu,
и
длиной 2b
= 2![]() ≈
2,82, параллельными осиОv,
в который и следует вписать эллипс:
≈
2,82, параллельными осиОv,
в который и следует вписать эллипс:

Записываем
с учетом произведенной замены переменных
координаты вершин А1(а
+ х0;
у0);
А2(–
а
+ х0;
у0);
В1(x0;
b
+ y0);
B2(x0;
– b
+ y0)
и фокусов F1(с
+ х0;
у0),
F2(–
с
+ х0;
у0)
эллипса, уравнения директрис х
=
![]() и находим значение эксцентриситета
этого эллипса ε
=
c/a.
и находим значение эксцентриситета
этого эллипса ε
=
c/a.
Вершины
эллипса: А1(![]() +
3; 2);
А2(–
+
3; 2);
А2(–![]() + 3; 2);
В1(3;
+ 3; 2);
В1(3;
![]() +
2);
B2(3;
–
+
2);
B2(3;
–![]() + 2).
+ 2).
Фокусы эллипса F1(5; 2), F2(1; 2).
Уравнения директрис: х = 6 и х = 0.
Эксцентриситет:
ε
=
2/![]() .
.
б)
В квадратичной форме уравнения кривой
4х2
+ у2
+ 16х
– 2у
+ 8 = 0: А
= 4, В
= 0, С
=
1, то определитель
=
![]() =
=![]() = 4 > 0. Следовательно, кривая, задаваемая
этим уравнением, – эллипс.
= 4 > 0. Следовательно, кривая, задаваемая
этим уравнением, – эллипс.
Выделим
полные квадраты переменных способом
Лагранжа. Для этого в уравнении кривой
группируем неизвестные: (4х2
+ 16х)
+ (у2–
2у)
+ 8 = 0. Поскольку 4х2
+ 16х
= 4(х2
+ 4х)
= 4(х2
+ 4х
+ 4) – 16 = 4(х
+ 2)2
– 16 и у2–
2у
= (у2
– 2у
+ 1) – 1 = (у
– 1)2
– 1, то уравнение кривой принимает вид:
4(х
+ 2)2
– 16 + (у
– 1)2
– 1 + 8 = 0, или 4(х
+ 2)2
+ (у
– 1)2
= 9. После деления полученного уравнения
на 9 и переноса всех коэффициентов при
переменных в знаменатели дробей получаем:
![]() =
1.
=
1.
Больший
знаменатель полученного уравнения
эллипса является параметром а2,
т.е. а2
= 9 и b2
= 2,25. Т.о., имеем: а
= 3; b
= 1,5; с
=
![]() =
=![]() =
=![]() =
=![]() ≈
2,6.
≈
2,6.
Поскольку
согласно полученному уравнению большая
ось 2а
эллипса параллельна оси Оу,
то ось Оu
![]() Оу
а ось Оv,
образуя с Оu
правую систему координат, направлена
противоположно оси Ох,
что соответствует
замене переменных: y
– y0
=
y
– 1 = u,
х
– х0
=
х
+ 2= – v.
В координатной системе Оuv
получаем каноническое уравнение эллипса:
Оу
а ось Оv,
образуя с Оu
правую систему координат, направлена
противоположно оси Ох,
что соответствует
замене переменных: y
– y0
=
y
– 1 = u,
х
– х0
=
х
+ 2= – v.
В координатной системе Оuv
получаем каноническое уравнение эллипса:
![]() =
1,
причем поскольку х0
= – 2, у0
= 1, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(–
2; 1).
=
1,
причем поскольку х0
= – 2, у0
= 1, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(–
2; 1).
Для построения эллипса чертим в координатной системе Оuv прямоугольник с центром в точке О и сторонами длиной 2а = 6, параллельными оси Оu, и длиной 2b = 3, параллельными оси Оv, в который и следует вписать эллипс:
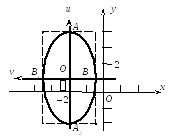
Записываем
с учетом произведенной замены переменных
координаты вершин А1(х0;
а
+ у0);
А2(х0;
– а
+ у0);
В1(–
b
+ х0;
у0);
B2(b
+ х0;
у0)
и фокусов F1(х0;
с
+ у0),
F2(х0;
– с
+ у0)
эллипса, уравнения директрис у
=
![]() и находим значение эксцентриситета
этого эллипса ε
=
c/a.
и находим значение эксцентриситета
этого эллипса ε
=
c/a.
Вершины эллипса: А1(– 2; 4); А2(– 2; – 2); В1(– 3,5; 1); B2(– 0,5; 1).
Фокусы
эллипса F1(–
2;
![]() +
1),
F2(–
2; –
+
1),
F2(–
2; –
![]() +
1).
+
1).
Уравнения
директрис: у
= 2![]() +
1 иу
= – 2
+
1 иу
= – 2![]() +
1.
+
1.
Эксцентриситет:
ε
=
![]() /2.
/2.
в)
В квадратичной форме уравнения кривой
х2
– у2
+ 6х
–
2у
+ 6 = 0: А
= 1, В
= 0, С
=
– 1, то определитель
=
![]() =
=![]() = – 1 < 0. Следовательно, кривая, задаваемая
этим уравнением, – гипербола.
= – 1 < 0. Следовательно, кривая, задаваемая
этим уравнением, – гипербола.
Выделим
полные квадраты переменных способом
Лагранжа. Для этого в уравнении кривой
группируем неизвестные: (х2
+ 6х)
– (у2+
2у)
+ 6 = 0. Поскольку х2
+ 6х
= (х2
+ 6х
+ 9) – 9 = (х
+ 3)2
– 9 и у2+
2у
= (у2
+ 2у
+ 1) – 1 = (у
+ 1)2
– 1, то уравнение кривой принимает вид:
(х
+ 3)2
– 9 – (у
+ 1)2
+ 1 + 6 = 0, или (х
+ 3)2
– (у
+ 1)2
= 2. После деления полученного уравнения
на 2 получаем:
![]() =
1.
=
1.
Поскольку
согласно полученному уравнению
действительная ось гиперболы параллельна
оси Ох,
то ось Оu
![]() Ох
а ось Оv,
образуя с Оu
правую систему координат, сонаправлена
оси Оу,
что соответствует
замене переменных: х
– х0
=
х
+ 3 = u,
y
– y0
=
y
+ 1 = v.
В координатной системе Оuv
получаем каноническое уравнение
гиперболы
Ох
а ось Оv,
образуя с Оu
правую систему координат, сонаправлена
оси Оу,
что соответствует
замене переменных: х
– х0
=
х
+ 3 = u,
y
– y0
=
y
+ 1 = v.
В координатной системе Оuv
получаем каноническое уравнение
гиперболы
![]() =
1:
=
1:
![]() =
1,
причем поскольку х0
= – 3, у0
= –1, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(–
3; – 1).
=
1,
причем поскольку х0
= – 3, у0
= –1, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(–
3; – 1).
Действительной
оси гиперболы соответствует знаменатель
а2,
т.е. а2
= 2. В рассматриваемом примере и b2
= 2. Т.о., имеем: а
=
![]() ≈
1,41;
b
=
≈
1,41;
b
=
![]() ≈
1,41;
с
=
≈
1,41;
с
=
![]() =
=![]() =
2.
=
2.
Д ля
построения гиперболы чертим в координатной
системеОuv
прямоугольник
с центром в точке О
и сторонами длиной 2а
= 2
ля
построения гиперболы чертим в координатной
системеОuv
прямоугольник
с центром в точке О
и сторонами длиной 2а
= 2![]() ≈ 2,82, параллельными осиОu,
и
длиной 2b
= 2
≈ 2,82, параллельными осиОu,
и
длиной 2b
= 2![]() ≈
2,82, параллельными осиОv
(т.е. в данном примере прямоугольник
является квадратом). Проводим диагонали
этого прямоугольника и вписываем между
ними вне прямоугольника ветви гиперболы,
вершины которой должны касаться боковых
сторон прямоугольника:
≈
2,82, параллельными осиОv
(т.е. в данном примере прямоугольник
является квадратом). Проводим диагонали
этого прямоугольника и вписываем между
ними вне прямоугольника ветви гиперболы,
вершины которой должны касаться боковых
сторон прямоугольника:
Записываем
с учетом произведенной замены переменных
координаты вершин А1(а
+ х0;
у0);
А2(–
а
+ х0;
у0);
фокусов F1(с
+ х0;
у0),
F2(–
с
+ х0;
у0)
гиперболы, уравнения асимптот у
=
![]() +у0,
директрис х
=
+у0,
директрис х
=
![]() и находим значение эксцентриситета
этой гиперболы ε
=
c/a.
и находим значение эксцентриситета
этой гиперболы ε
=
c/a.
Вершины
гиперболы: А1(![]() –
3; – 1);
А2(–
–
3; – 1);
А2(–![]() – 3; – 1).
– 3; – 1).
Фокусы гиперболы F1(– 1; – 1), F2(– 5; – 1).
Уравнения асимптот: у = х + 2; у = – х – 4.
Уравнения директрис: х = – 2 и х = – 4.
Эксцентриситет:
ε
=
2/![]() =
=![]() .
.
г)
В квадратичной форме уравнения кривой
5х2
– 4у2
+ 10х
+
16у
+ 9 = 0: А
= 5, В
= 0, С
=
– 4, то определитель
=
![]() =
=![]() = – 20 < 0. Следовательно, кривая, задаваемая
этим уравнением, – гипербола.
= – 20 < 0. Следовательно, кривая, задаваемая
этим уравнением, – гипербола.
Выделим
полные квадраты переменных способом
Лагранжа. Для этого в уравнении кривой
группируем неизвестные: (5х2
+ 10х)
– (4у2–
16у)
+ 9 = 0. Поскольку 5х2
+ 10х
= 5(х2
+ 2х)
= 5(х2
+ 2х
+ 1) – 5 = 5(х
+ 1)2
– 5 и 4у2–
16у
= 4(у2
– 4у)
= 4(у2
– 4у
+ 4) – 16 = 4(у
– 2)2
– 16, то уравнение кривой принимает вид:
5(х
+ 1)2
– 5 – 4(у
– 2)2
+ 16 + 9 = 0, или 5(х
+ 1)2
– 4(у
– 2)2
= –20. После деления полученного уравнения
на (– 20) получаем:
![]() =
1.
=
1.
Поскольку
согласно полученному уравнению
действительная ось гиперболы параллельна
оси Оу,
то ось Оu
![]() Оу
а ось Оv,
образуя с Оu
правую систему координат, направлена
противоположно оси Ох,
что соответствует
замене переменных: у
– у0
=
у
– 2 = u,
х
– х0
=
х
+ 1 = – v.
В координатной системе Оuv
получаем каноническое уравнение
гиперболы
Оу
а ось Оv,
образуя с Оu
правую систему координат, направлена
противоположно оси Ох,
что соответствует
замене переменных: у
– у0
=
у
– 2 = u,
х
– х0
=
х
+ 1 = – v.
В координатной системе Оuv
получаем каноническое уравнение
гиперболы
![]() =
1:
=
1:
![]() =
1,
причем поскольку х0
= – 1, у0
= 2, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(–
1; 2).
=
1,
причем поскольку х0
= – 1, у0
= 2, то центр
этой координатной системы О(х0;
у0)
соответствует точке О(–
1; 2).
Действительной
оси гиперболы соответствует знаменатель
а2,
т.е. а2
= 5, b2
= 4. Т.о., имеем: а
=
![]() ≈
2,24;
b
= 2; с
=
≈
2,24;
b
= 2; с
=
![]() =
=![]() =
3.
=
3.
Д ля
построения гиперболы чертим
ля
построения гиперболы чертим
в координатной системе Оuv прямоу-
гольник с центром в точке О и сторо-
нами
длиной 2а
= 2![]() ≈ 4,48, парал-
≈ 4,48, парал-
лельными оси Оu, и длиной 2b = 4,
параллельными оси Оv. Проводим
диагонали этого прямоугольника и
вписываем между ними вне прямоу-
гольника ветви гиперболы, вершины
которой должны касаться боковых
сторон прямоугольника:
Записываем
с учетом произведенной замены переменных
координаты вершин А1(х0;
а
+ у0);
А2(х0;
– а
+ у0);
фокусов F1(х0;
с
+ у0),
F2(х0;
– с
+ у0)
гиперболы, уравнения асимптот у
=
![]() +у0,
директрис y
=
+у0,
директрис y
=
![]() и находим значение эксцентриситета
этой гиперболы ε
=
c/a.
и находим значение эксцентриситета
этой гиперболы ε
=
c/a.
Вершины
гиперболы: А1(–
1;
![]() +
2);
А2(–
1; –
+
2);
А2(–
1; –![]() + 2).
+ 2).
Фокусы гиперболы F1(– 1; 5), F2(– 1; – 1).
Уравнения
асимптот: у
=
![]() (х
+ 1) + 2; у
= –
(х
+ 1) + 2; у
= –
![]() (х
+ 1) + 2.
(х
+ 1) + 2.
Уравнения директрис: y = 11/3 и y = 1/3.
Эксцентриситет:
ε
=
3/![]() .
.
3. Составить уравнение кривой второго порядка, если: а) МА : МВ = 0,8; б) МА = МВ, где МА – расстояние от переменной точки М на кривой до точки А(2; 1), МВ – расстояние от точки М до прямой х = – 5.
Решение.
Задаем
точку М
на кривой переменными координатами:
М(х;
у),
тогда получаем на плоскости три точки:
А(2;
1), М(х;
у),
В(–
5; у).
Находим: МА
=
![]() ,МВ
=
,МВ
=
![]() =
=![]() =
|x
+ 5|.
=
|x
+ 5|.
а)
По условию МА
:
МВ
= 0,8, т.е.
![]() = 0,8|x
+ 5|.
= 0,8|x
+ 5|.
При
возведении обеих части уравнения в
квадрат получим: (х
– 2)2
+ (у
– 1)2
= 0,64(х
+ 5)2,
откуда х2
– 4х
+ 4 + у2
– 2у
+ 1 = 0,64х2
+ 6,4х
+ 16, или 0,36х2
+ у2
–
10,4х
– 2y
– 11 = 0. По знаку дискриминанта
=
![]() =
=![]() = 0,36
> 0, определяем, что данная кривая –
эллипс.
= 0,36
> 0, определяем, что данная кривая –
эллипс.
б)
По условию МА
=
МВ,
т.е.
![]() =
|x
+ 5|.
=
|x
+ 5|.
При возведении обеих части уравнения в квадрат получим: (х – 2)2 + (у – 1)2 = (х + 5)2, откуда х2 – 4х + 4 + у2 – 2у + 1 = х2 + 10х + 25, или у2 – 14х – 2y – 20 = 0.
Поскольку
дискриминант
=
![]() =
=![]() = 0, то данная кривая – парабола.
= 0, то данная кривая – парабола.
Ответ: а) 0,36х2 + у2 – 10,4х – 2y – 11 = 0; б) у2 – 14х – 2y – 20 = 0.
4. Составить уравнение окружности, если: а) ее центр находится на оси Оу и она проходит через точки А(2; 1) и В(3; − 4); б) ее диаметром служит отрезок прямой 2x − 3y + 6 = 0, содержащийся между осями координат; в) ее диаметром служит общая хорда окружностей: х2 + у2 – 4х – 12у + 8 = 0, х2 + у2 – 6х – 16у + 12 = 0; г) она проходит через точку А(− 2; 1) и является концентрической по отношению к окружности х2 + у2 – 4х + 2у – 11 = 0.
Решение.
а)
Точки А(2;
1) и В(3;
− 4) находятся на окружности. По условию
центр окружности находится на оси Оу.
Следовательно, центр окружности – точка
С(0;
у).
Найдем неизвестную координату центра
окружности и квадрат радиуса окружности
R2
из
равенств: СА
= СВ
= R.
Поскольку СА
=![]() =
=![]() ,СВ
=
,СВ
=![]() =
=![]() ,
то 4 + (1 –у)2
= 9 + (4 + у)2,
откуда 5 – 2у
+ у2
= 25 + 8у
+ у2,
и, следовательно, 10у
= – 20, т.е. у
=
– 2. Квадрат радиуса окружности R2
= (СА)2
= 4 + (1 –(– 2))2
= 13. Составляем уравнение окружности,
квадрат радиуса которой R2
= 13, и центр которой в точке С(0;
– 2): х2
+ (у
+ 2)2
= 13, или х2
+ у2
+ 2у
– 9 = 0.
,
то 4 + (1 –у)2
= 9 + (4 + у)2,
откуда 5 – 2у
+ у2
= 25 + 8у
+ у2,
и, следовательно, 10у
= – 20, т.е. у
=
– 2. Квадрат радиуса окружности R2
= (СА)2
= 4 + (1 –(– 2))2
= 13. Составляем уравнение окружности,
квадрат радиуса которой R2
= 13, и центр которой в точке С(0;
– 2): х2
+ (у
+ 2)2
= 13, или х2
+ у2
+ 2у
– 9 = 0.
б)
Находим точки пересечения прямой 2x
−
3y
+
6 = 0 с осями координат. Координаты точки
А
пересечения
прямой с осью Ох
определяются из системы
![]() т.е.А(–
3; 0). Координаты точки В
пересечения
прямой с осью Оу
определяются из системы
т.е.А(–
3; 0). Координаты точки В
пересечения
прямой с осью Оу
определяются из системы
![]() т.е.В(0;
2). Центр отрезка АВ
является центром окружности С.
Координаты точки С
находим как средние арифметические
соответствующих координат концов
отрезка: С(–
1,5; 1). Длина отрезка АВ
=
т.е.В(0;
2). Центр отрезка АВ
является центром окружности С.
Координаты точки С
находим как средние арифметические
соответствующих координат концов
отрезка: С(–
1,5; 1). Длина отрезка АВ
=
![]() =
=![]() – удвоенный радиус окружности, т.е.
радиус окружностиR
=
– удвоенный радиус окружности, т.е.
радиус окружностиR
=
![]() /2.
/2.
Составляем
уравнение окружности по ее радиусу R
=
![]() /2
и координатам центраС(–
1,5; 1): (х
+ 1,5)2
+ (у
– 1)2
= 13/4.
/2
и координатам центраС(–
1,5; 1): (х
+ 1,5)2
+ (у
– 1)2
= 13/4.
в)
Находим координаты точек А
и В,
которые являются концевыми точками
общей хорды окружностей х2
+ у2
– 4х
– 12у
+ 8 = 0, х2
+ у2
– 6х
– 16у
+ 12 = 0. Для этого решаем систему уравнений:
![]() Если из 1-го уравнения вычесть 2-е, то
получим равносильную систему:
Если из 1-го уравнения вычесть 2-е, то
получим равносильную систему:![]() или
или![]()
Подставляем
это выражение для х
в 1-е уравнение: (2 – 2у)2
+ у2
– 4(2 – 2у)
– 12у
+ 8 = 0, или 5у2
– 12у
+ 4 = 0, откуда у1
= 2; у2
= 0,4. Следовательно, х1
= 2 – 2у1
= – 2; х2
= 2 – 2у2
= 1,2. Т.о., получены две концевые точки
хорды: А(–
2; 2), В(1,2;
0,4). Центр окружности С
находится
в центре этой хорды, следовательно,
координаты центра окружности находим
как среднее арифметическое соответствующих
координат точек А
и
В:
С(–
0,4; 1,2). Длина отрезка АВ
=
![]() =
=![]() = 2
= 2![]() ,
следовательно, радиус окружности равенR
= AB/2
=
,
следовательно, радиус окружности равенR
= AB/2
=
![]() .
.
Составляем
уравнение окружности по ее радиусу R
=
![]() и координатам центраС(–
0,4; 1,2): (х
+ 0,4)2
+ (у
– 1,2)2
= 3,2.
и координатам центраС(–
0,4; 1,2): (х
+ 0,4)2
+ (у
– 1,2)2
= 3,2.
г) Известно, что искомая окружность проходит через точку А(− 2; 1) и является концентрической по отношению к окружности х2 + у2 – 4х + 2у – 11 = 0.
Находим центр окружности х2 + у2 – 4х + 2у – 11 = 0, выделив полные квадраты переменных способом Лагранжа. Для этого группируем неизвестные: (х2 – 4х) + (у2 + 2у) – 11 = 0. Поскольку х2 – 4х = (х2 – 4х + 4) – 4 = (х – 2)2 – 4, у2 + 2у = (у2 + 2у + 1) – 1 = (у + 1)2 – 1, то уравнение заданной окружности принимает вид: (х – 2)2 – 4 + (у + 1)2 – 1 – 11 = 0, или (х – 2)2 + (у + 1)2 = 16. Т.о., центром этой окружности является точка С(2; – 1).
Согласно
условию точка С(2;
– 1) является центром и искомой окружности.
Найдем
радиус искомой окружности R
как длину отрезка СА
=
![]() =
=![]() .
.
Составляем
уравнение окружности по ее радиусу R
=
![]() и координатам центраС(2;
– 1): (х
– 2)2
+ (у
+ 1)2
= 20, или х2
+ у2
– 4х
+2у
– 15 = 0.
и координатам центраС(2;
– 1): (х
– 2)2
+ (у
+ 1)2
= 20, или х2
+ у2
– 4х
+2у
– 15 = 0.
Ответ: а) х2 + у2 + 2у – 9 = 0; б) (х + 1,5)2 + (у – 1)2 = 13/4; в) (х + 0,4)2 + (у – 1,2)2 = 3,2; г) х2 + у2 – 4х +2у – 15 = 0.
5. Точка А(– 2; 3) принадлежит окружности, задаваемой уравнением х2 + у2 + 2х – 4у + 3 = 0. Составить уравнение: а) радиуса окружности этой окружности, проведенного в точку А; б) касательной к этой окружности, проведенной через точку А.
Решение.
а) Находим координаты центра окружности х2 + у2 + 2х – 4у + 3 = 0. Для этого выделяем в уравнении полные квадраты способом Лагранжа. Сначала группируем переменные: (х2 + 2х) + (у2– 4у) + 3 = 0. Поскольку х2 + 2х = (х2 + 2х + 1) – 1 = (х + 1)2 – 1; у2– 4у = (у2– 4у + 4) – 4 = (у – 2)2 – 4, то уравнение окружности примет вид: (х + 1)2 – 1 + (у – 2)2 – 4 + 3 = 0, или (х + 1)2 + (у – 2)2 = 2. Следовательно, центром этой окружности служит точка С(– 1; 2).
Находим уравнение прямой, проходящей через точки А(– 2; 3) и С(– 1; 2):
![]() ,
или х
+ у
– 1 = 0.
,
или х
+ у
– 1 = 0.
б) Находим уравнение касательной, проведенной через точку А(– 2; 3), лежащей на окружности х2 + у2 + 2х – 4у + 3 = 0. Как и в задаче (5а) сначала находим координаты центра С этой окружности. Согласно полученному результату центр окружности находится в точке С(– 1; 2). Определяем вектор N = AC = {1; – 1}, который является нормальным к искомой касательной. Составляем уравнение касательной по нормальному вектору N = {1; – 1} и точке А(– 2; 3), через которую эта касательная проходит:
(х + 2) – (у – 3) = 0, или х – у + 5 = 0.
Ответ: а) х + у – 1 = 0; б) х – у + 5 = 0.
6. Составить уравнение: а) параболы, фокус которой лежит в точке F(0; 0), а директриса задана уравнением у = – 2; б) директрисы параболы х2 + 6х – 8у + 1 = 0; в) оси параболы у2 – 8у + 4х – 4 = 0.
Решение.
а) Дано: директриса параболы задана уравнением у = – 2, фокус параболы F(0; 0).
Поскольку директриса параболы перпендикулярна оси Оу, а фокус лежит на оси Оу и находится выше директрисы, то осью параболы является ось Оу и ветви параболы направлены вверх.
Вершина А параболы находится на оси Оу посередине между фокусом F(0; 0)и точкой пересечения директрисы с осью Оу, т.е. точкой (0; – 2). Следовательно, А(0; – 1), фокальный параметр параболы р = 2, а уравнение параболы будет иметь вид: х2 = 2р (у – у0), где у0 – ордината вершины параболы, т.е. ордината точки А(0; – 1), следовательно, у0 = – 1. Т.о., уравнение параболы: х2 = 4 (у + 1), или х2 – 4у –4 = 0.
б) Найдем уравнение директрисы параболы х2 + 6х – 8у + 1 = 0.
Выделим полный квадрат для переменной х: (х2 + 6х) = 8у – 1; (х2 + 6х + 9) – 9 = 8у – 1; (х + 3)2 = 8(у + 1).
Перейдем к новым переменным: u = x + 3; v = y + 1. В этих переменных уравнение параболы примет вид u2 = 8v, следовательно, фокальный параметр параболы р = 4, а уравнение директрисы v = – p/2, т.е. v = – 2. Уравнение директрисы при возвращении к исходным переменным: y + 1 = – 2, или у = – 3.
в) Найдем уравнение оси параболы у2 – 8у + 4х – 4 = 0.
Выделим полный квадрат для переменной у: (у2 – 8у) = – 4х + 4; (у2 – 8у + 16) – 16 = – 4х + 4; (у – 4)2 = 4(– х + 5).
Перейдем к новым переменным: u = – x + 5; v = y – 4. В этих переменных уравнение параболы примет вид v2 = 4u, следовательно, уравнение оси параболы в новых переменных v = 0. Уравнение этой оси при возвращении к исходным переменным: y – 4 = 0, или у = 4.
Ответ: а) у = – 3; б) у = 4.
7. Составить уравнение эллипса с центром в начале координат и фокусами на оси Ох, если: а) расстояние между фокусами равно 4,8, а эксцентриситет равен 0,8; б) если эллипс проходит через точки А(3; 1) и В(2; – 2).
Решение.
а)
Дано: 2с =
4,8;
= 0,8. Из с
= 2,4 и
= с/а
= 0,8 находим большую полуось эллипса а
= с/
= 2,4/0,8 = 3. Из равенства с
=
![]() находим квадрат меньшей полуоси эллипса
b2
= a2
– c2
= 9 – 2,42
= 3,24, т.е. b
= 1,8. Т.о., уравнение эллипса будет иметь
вид:
находим квадрат меньшей полуоси эллипса
b2
= a2
– c2
= 9 – 2,42
= 3,24, т.е. b
= 1,8. Т.о., уравнение эллипса будет иметь
вид:![]() .
.
б)
Подставляем координаты точек А(3;
1) и В(2;
–
2) в уравнение
эллипса
![]() ,
получаем систему уравнений для определенияа2
и b2:
,
получаем систему уравнений для определенияа2
и b2:
![]() Чтобы решить систему введем обозначения
1/а2
= u,
1/b2
= v.
Решаем систему
Чтобы решить систему введем обозначения
1/а2
= u,
1/b2
= v.
Решаем систему
![]() по
формулам Крамера: определитель системы
=
по
формулам Крамера: определитель системы
=
![]() = 32; определитель для неизвестнойu
равен 1
=
= 32; определитель для неизвестнойu
равен 1
=
![]() = 3; определитель для неизвестнойv
равен 2
=
= 3; определитель для неизвестнойv
равен 2
=
![]() = 5. Следовательно, 1/а2
= u
= 5. Следовательно, 1/а2
= u
= 3/32; 1/b2
= v
= 5/32, и уравнение эллипса принимает вид:
![]() ,
или 3х2
+ 5у2
= 32.
,
или 3х2
+ 5у2
= 32.
Ответ:
а)
![]() ;б) 3х2
+ 5у2
= 32.
;б) 3х2
+ 5у2
= 32.
8.
Составить уравнение гиперболы, если:
а)
расстояние между фокусами, расположенными
на оси Ох,
равно 30, а уравнения асимптот у
=
2х;
б)
если одна из ее ветвей проходит через
точку М(2;
– 2), а уравнения асимптот у
=
![]() х;
в)
ее центр расположен в начале координат,
фокусы – на оси Ох,
и она проходит через точки А(–
5; 3) и В(4;
– 2); г)
ее фокусы расположены на оси Оу,
она равносторонняя и одна из ветвей
проходит через точку М(2;
– 6).
х;
в)
ее центр расположен в начале координат,
фокусы – на оси Ох,
и она проходит через точки А(–
5; 3) и В(4;
– 2); г)
ее фокусы расположены на оси Оу,
она равносторонняя и одна из ветвей
проходит через точку М(2;
– 6).
Решение.
а)
Дано: 2с
= 30; у
=
![]() =
2х.
Следовательно, получаем систему уравнений
для определения параметров а2
и b2
искомого уравнения гиперболы
=
2х.
Следовательно, получаем систему уравнений
для определения параметров а2
и b2
искомого уравнения гиперболы
![]() ,
оси которой расположены на осиОх,
а асимптоты пересекаются в начале
координат:
,
оси которой расположены на осиОх,
а асимптоты пересекаются в начале
координат:
с2 = а2 + b2 = 152 = 225; b = 2a, или b2 = 4a2.
В
результате получаем 5а2
=
225, а2
=
45; b2
=
180, и поэтому
уравнение гиперболы:
![]() .
.
б) Дано: одна из ветвей гиперболы проходит через точку М(2; – 2), уравнения асимптот гиперболы у = х/4.
Поскольку
асимптоты гиперболы пересекаются в
начале координат, но в условии задания
не указана ось, на которой находятся
фокусы гиперболы, то ее искомое уравнение
пока следует записать в общем виде:
![]() .
.
Поскольку
гипербола проходит через точку М(2;
– 2), то должно выполняться равенство:
![]() ,
или
,
или![]() .
Из уравнения асимптоту
=
.
Из уравнения асимптоту
=
![]() =
=
![]() получаема
= 4b,
или а2
= 16b2.
Следовательно,
получаема
= 4b,
или а2
= 16b2.
Следовательно,
![]() ,
или
,
или![]() ,
или
,
или![]() ,
откуда заключаем, что в правой части
уравнения следует брать знак минус, и
при этомb2
= 15/4, а а2
= 16b2
= 60. В результате получаем, что уравнение
гиперболы имеет вид:
,
откуда заключаем, что в правой части
уравнения следует брать знак минус, и
при этомb2
= 15/4, а а2
= 16b2
= 60. В результате получаем, что уравнение
гиперболы имеет вид:
![]() ,
или
,
или![]() .
.
в) Дано: центр гиперболы расположен в начале координат, фокусы – на оси Ох, и гипербола проходит через точки А(– 5; 3) и В(4; – 2).
Согласно
условию уравнение гиперболы должно
иметь вид:
![]() .
.
Подставляя координаты точек А(– 5; 3) и В(4; – 2) в уравнение, получим систему для определения параметров а2 и b2 искомого уравнения гиперболы:
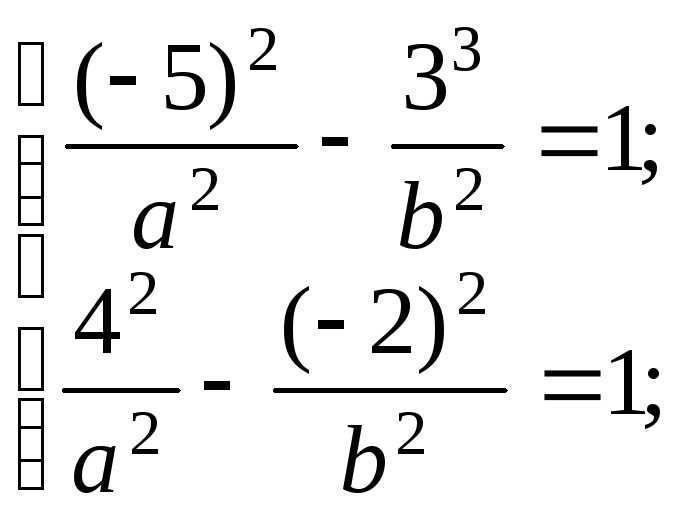 или,
обозначая u
= 1/a2,
v
= 1/b2,
получаем эту систему в виде:
или,
обозначая u
= 1/a2,
v
= 1/b2,
получаем эту систему в виде:
![]() Решаем
систему по формулам Крамера:
=
Решаем
систему по формулам Крамера:
=
![]() = 44;1
=
= 44;1
=
![]() = 5;2
=
= 5;2
=
![]() = 9;u
= 1/a2
= 1/
= 5/44; v
= 1/b2
= 2/
= 9/44. Следовательно, a2
= 44/5; b2
= 44/9, и искомое уравнение гиперболы:
= 9;u
= 1/a2
= 1/
= 5/44; v
= 1/b2
= 2/
= 9/44. Следовательно, a2
= 44/5; b2
= 44/9, и искомое уравнение гиперболы:
![]() ,
или 5х2
– 9у2
= 44.
,
или 5х2
– 9у2
= 44.
г) Дано: фокусы равносторонней гиперболы расположены на оси Оу, и одна из ее ветвей проходит через точку М(2; – 6).
Согласно
условию уравнение гиперболы должно
иметь вид:
![]() ,
илиу2
–
х2
=
а2.
,
илиу2
–
х2
=
а2.
Подставляя
координаты точки М(2;
– 6) в уравнение, определим параметр а2
искомого уравнения гиперболы: (– 6)2
– 22
= а2,
т.е. а2
= 32. Т.о., уравнение равносторонней
гиперболы имеет вид:
![]() ,
илиу2
–
х2
=
32.
,
илиу2
–
х2
=
32.
Ответ:
а)
![]() ;б)
;б)
![]() ;в)
5х2
– 9у2
= 44; г)
у2
–
х2
=
32.
;в)
5х2
– 9у2
= 44; г)
у2
–
х2
=
32.
9.
Найти эксцентриситет: а)
эллипса
![]() ;
б)
гиперболы
;
б)
гиперболы
![]() .
.
Решение.
а)
Согласно уравнению эллипса
![]() имеем:а2
= 81; b2
= 56. Находим эксцентриситет эллипса,
большая ось которого находится на
координатной оси Ох:
= с/а
=
имеем:а2
= 81; b2
= 56. Находим эксцентриситет эллипса,
большая ось которого находится на
координатной оси Ох:
= с/а
=
![]() /а
=
/а
=
![]() /
/![]() =
=![]() /
/![]() = 5/9.
= 5/9.
б)
Согласно уравнению гиперболы
![]() имеем:а2
= 49; b2
= 15. Находим эксцентриситет гиперболы,
действительная ось которого находится
на координатной оси Ох:
= с/а
=
имеем:а2
= 49; b2
= 15. Находим эксцентриситет гиперболы,
действительная ось которого находится
на координатной оси Ох:
= с/а
=
![]() /а
=
/а
=
![]() /
/![]() =
=![]() /
/![]() = 8/7.
= 8/7.
Ответ: а) 5/9; б) 8/7.
