2 Лаплас түрлендіруінің қасиеттері

Теорема 2.1 Түрлендірудің сызықтылығы

Егер функциялары түпнұсқалар, ал олардың бейнелері тиісіншежәнешамалары t-мен р-ға тәуелсіз болса, онда мына арақатынастар орындалады:

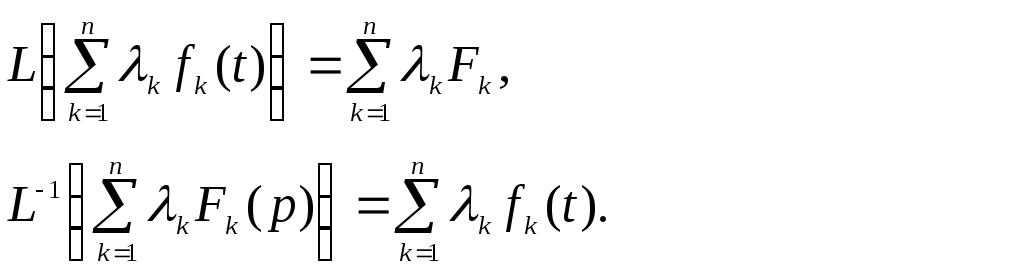(17)

Шынында да, (1.1) формулаға сәйкес

Егер интегралыфункциялары үшінжарты жазықтығында жинақталса, онда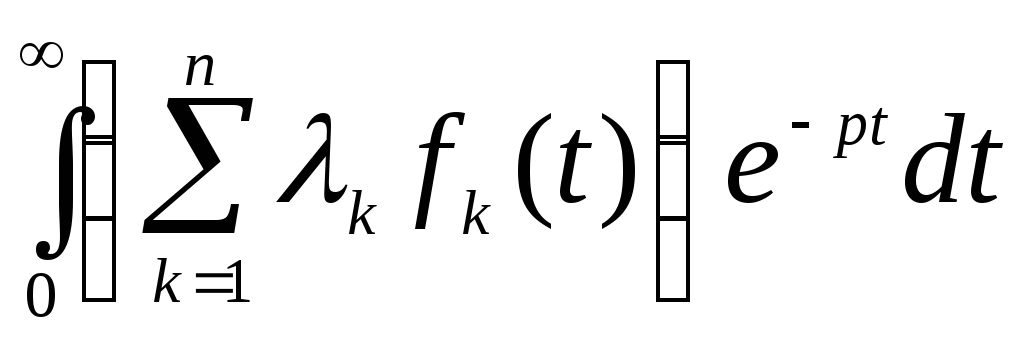интегралыжарты жазықтығында жинақталады.

5 Мысал

функцияларының бейнесін табу керек.

Мұндағы ω-нақты немесе комплекс сан.

Шешуі

Комплекс айнымалының функциясының теориясынан белгілі формулаларды жазайық:

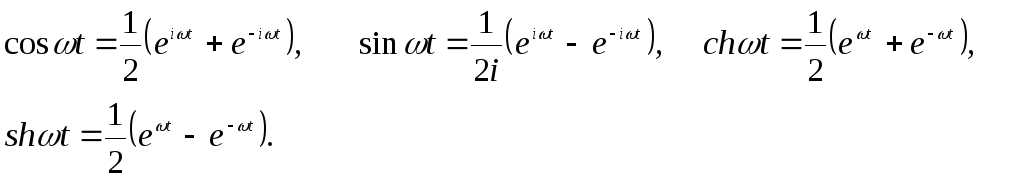
Бейненің сызықтылығын және (9) формуласын пайдаланып керекті сәйкестіктерді аламыз.

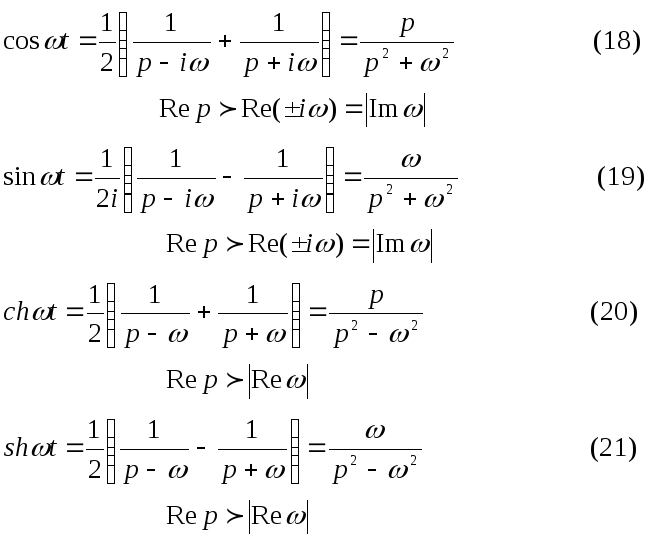
6 Мысал

функцияларының бейнесін табу керек.

Мұндағы ω, φ-кез-келген нақты немесе комплекс сандар.

Шешуі

Белгілі формулаларды жазайық:

Бейненің сызықтылығын және (18), (19) формулаларды пайдаланып мына сәйкестіктерді аламыз:

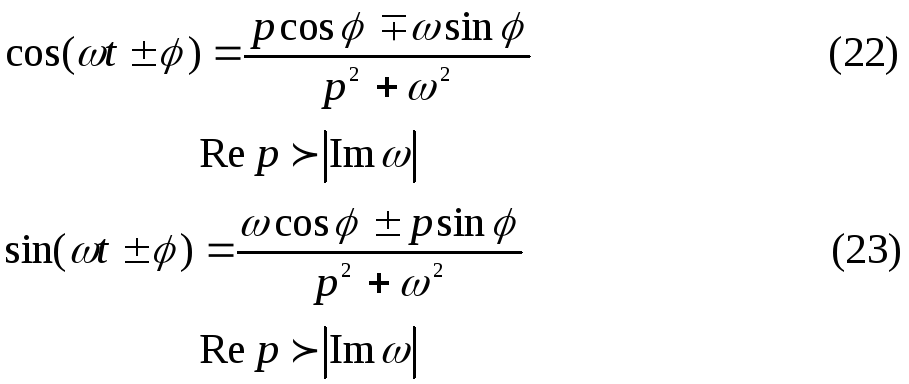
Теорема 2.2 Түпнұсқаны дифференциалдау

Егер өсу көрсеткіші болатынфункциясы мен оныңтуындысы түпнұсқалар, алфункциясытүпнұсқасының бейнесі болса, онда мынадай сәйкестік орындалады:

Дербес жағдайда, егер болса, онда

(25)

Дәлелдеу үшін интегралын бөліктеп интегралдаймыз:

Ал болғандықтан

бағалауын аламыз.

Сондықтан болады дасәйкестігін аламыз.

Бұл қасиетті жалпылауға болады.

Егер өсу көрсеткіші болатынтуындылары түпнұсқа болса, онда мынадай сәйкестіктер алуға болады:

(26)

Дербес жағдайда, егер болса, онда

(27)

7 Мысал

функциясының бейнесін табу керек.

Шешуі

болсын дейік. Сонда

Бірақ болғандықтан

Сонымен

Осыдан аламыз.

Осы нәтижені теңдігі арқылы да алуға болады.

Теорема 2.3 Түпнұсқаны интегралдау

Егер -түпнұсқа, алоның бейнесі болса, онда

Дәлелдеу үшін деп белгілейік те, түпнұсқаны дифференциалдау теоремасын пайдаланайық. Сондаалынады.

Егер сәйкестігін белгілесекдеп жазуға болады. Мұндаекендігі ескерілген. Алболғандықтансәйкестігі шығады. Осыданяғни

(29)

8 Мысал

функциясының бейнесін табу керек.

Шешуі

(9) формуланы пайдаланамыз

Түпнұсқаны интегралдау формуласы бойынша берілген функцияның бейнесін табамыз.

Теорема 2.4 Ұқсастық теоремасы

Егер -түпнұсқа, алоның бейнесі болса, онда

Мұндағы α-кез-келген сан. Шынында да анықтама бойынша

Интегралды ауыстыруын қолданып түрлендіреміз. Сонда мынадай нәтиже аламыз:

9 Мысал

функцияларының бейнелерін табу керек.

Шешуі

Ұқсастық теоремасын, яғни (30) формуланы пайдаланып, берілген функциялардың бейнелерін табамыз:

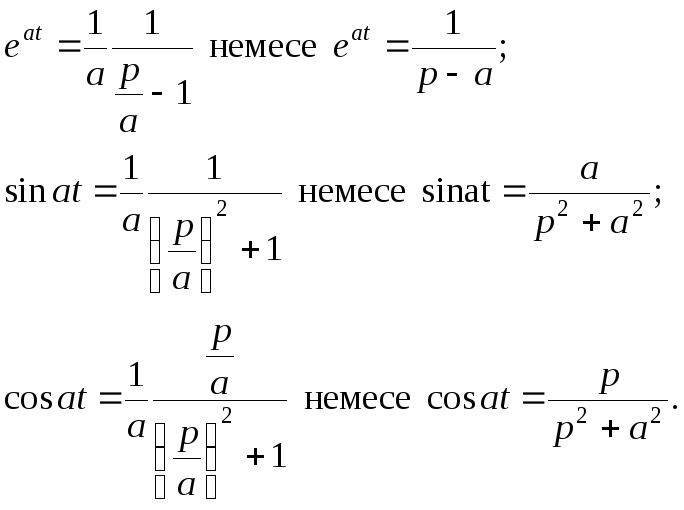
Терема 2.5 Кешеуілдеу теоремасы

Егер және-түпнұсқа болса, онда

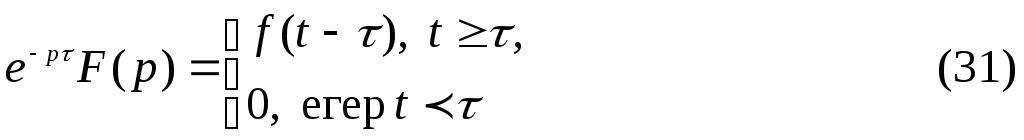
Дәлелдеу

Мына интегралындаауыстыруын қолданып түрлендіреміз. Сонда

Мұнда болғандаболғандықтантеңдігі орындалады.

Осыдан шығады да, теорема дәлелденеді.

“Кешеуілдеу” терминінің мағынасына тоқталайық.

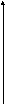
0 t 0 (τ,0) t

2.1 сурет 2.2 сурет

2.1 суретте функциясының графигі. Ал 2.2 суреттефункциясының графигі.функциясының графигіне қарағанда t осінің оң бағыты бойынша τ шамасына жылжытылған. Осыданфункциясымен сипатталатын құбылысфункциясымен сипатталатын құбылысқа қарағанда τ уақытқа кештеу басталатындығы көрінеді.