§2.1.11 Многочлены с целыми коэффициентами

Наибольший общий делитель всех коэффициентов многочлена с целыми коэффициентами называется его содержанием.Многочлен называетсяпримитивным, если его содержание равно 1.

Теорема (лемма Гаусса). Произведение примитивных многочленов вновь примитивный многочлен.

Доказательство: Пустьмногочленыgиhпримитивные, и простое числоpделит все коэффициенты многочленаf. Предположим, чтоk– номер первого коэффициента многочленаg, который не делится наp, аs– номер последнего коэффициента многочленаh, который не делится наp. Тогда в равенстве

число, стоящее слева и все слагаемые суммы, стоящей справа, кроме одного делятся наp. Противоречие. Следовательно, такого простого числаpнет и наибольший общий делитель коэффициентов многочленаfравен 1. ■

Теорема(признак Эйзенштейна). Если существует такое простое числоp, которое делит все коэффициенты многочлена с целыми коэффициентамикроме старшегоно для которого свободный членне делится нато многочленнеприводим.

Доказательство:Предположим противное, что многочленпредставлен в виде произведения двух многочленов с целыми коэффициентами

где

Тогда

Произведение делится наp, но не делится наВ силу простоты числаp, это означает, что один из сомножителей делится наp, скажема другой нет. Аналогичные рассуждения при рассмотрении равенства

но с учетом того, что не делится наp, приводят к выводу, чтоделится наp. Продолжив рассуждения, получим:делится наp, а следовательно,делится наp. Противоречие с условием. Значит наше предположение неверно и теорема доказана. ■

Теорема.Если– рациональный корень многочлена с целыми коэффициентамитоделится наp,делится наqи для любого целого числаmделится наВ частности,делится нааделится на

Доказательство:тогда

Из этого равенства следует, что делится наp. Нот.е. по теореме Евклидаделится наp. Аналогично, так какделится наq,тоделится наq.

Разделим наПолучим

Домножим обе части равенства на Тогда

и нетрудно доказать, что

Подставим в обе части тождества вместо хчислоm. Получим

т.е. делится нацело наиqвзаимно просты, поэтомуделится на■

Пример.Доказать, что уравнениене имеет рациональных корней.

Решение:Если– рациональный корень, тоpможет равняться 1 или -1, аqсоответственно 1, 2, 4, 8 (знак корня относим к числителю). Рациональным корнем может быть только одно из чисел 1,ПустьТогдаИз числа подозреваемых исключаем 1, а также(так какf(1) не делится наС помощью числаf(2) = 53 аналогичным образом убедимся, что и остальные числа не удовлетворяют условиюf(2) делится нат.е. не являются корнями уравнения.

Упражнения и задачи

1. Доказать, что уравнение 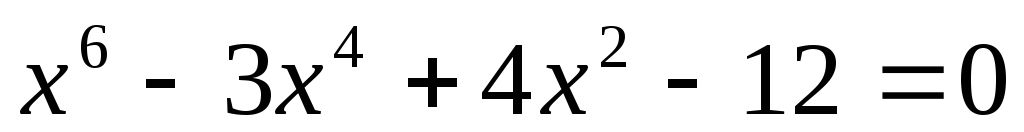не имеет рациональных корней.

2. Найти все рациональные корни многочленов:

а) б)

в) г)

§2.1.12 Многочлены с рациональными коэффициентами

Теорема.Многочлен с рациональными коэффициентами можно представить в виде произведения примитивного многочлена с целыми коэффициентами и несократимой рациональной дроби и притом единственным образом.

Доказательствотеоремы существования. Пустьb– наименьший общий знаменатель коэффициентов многочленас рациональными коэффициентами,а– содержание многочленас целыми коэффициентами. Тогдагде– примитивный многочлен с целыми коэффициентами. Отсюда

Доказательство теоремы единственности. Пусть игдеи– примитивные многочлены. Тогда

Отсюда так какad– содержание многочленааbc– содержание многочленаи эти многочлены равны. Следовательно,иОба представления совпали. Заметим, что в равенствечислаbиdположительны по построению. Докажем, чтоИз равенстваи условияпо теореме Евклида следует, чтоаделится нас, т.е.Подставив это значениеав равенство, получимилиbделится наd. А из того, что иаdделится наb,следует, чтоdделится наb. Положительные числаdиbделятся друг на друга, значит они равны,отсюда■