2.10. Теорема Штейнера

Предположим, что мы умеем вычислять моменты инерции относительно любой оси, проходящей через центр масс. Теперь возникает задача вычисления момента инерции тела относительно произвольной оси. Она решается с помощью теоремы Штейнера.

Эта теорема утверждает, что момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной ей оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения.

Для доказательства теоремы рассмотрим некую ось С, проходящую через центр масс ипараллельную ейосьО, отстоящую от осиСна расстоянииа. ОсьО может находиться и вне тела. Обе оси перпендикулярны плоскости чертежа (рис. 2.12).

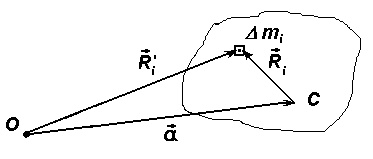
Рис. 2.12. К доказательству теоремы Штейнера

Из рис. 2.12 видно, что положение элемента массы относительно этих осей определяется векторамии, связь между которыми имеет вид:

Квадрат расстояния равен скалярному произведению

Тогда момент инерции тела относительно оси Оможно представить в следующем виде:

Последнее слагаемое в этом выражении есть момент инерции тела относительно оси, проходящей через центр масс. Обозначим его через Сумма. Напомним, что осиОиСпараллельны и следовательно, векторперпендикулярен осиС.Поэтому скалярное произведениеТаким образом, мы получаем:

(2.10.1)

\ 2.11. Уравнение движения твердого тела.

Абсолютно твердое тело имеет шесть степеней свободы и, следовательно, его движение описывается с помощью шести дифференциальных уравнений второго порядка. Три из них описывают движение центра масс твердого тела:

,,, (2.11.1)

где — координаты центра масс тела,— проекции внешних сил на оси координат,m — масса тела. Три других являются уравнениями моментов относительно осей ОХ, ОУ и ОZ в декартовой системе координат:

,,, (2.11.2)

где L_x, L_y, L_z — моменты импульса системы относительно осей ОХ, ОУ, ОZ, а M_x, M_y, M_z — моменты внешних сил относительно этих же осей.

Если перемещать точку приложения силы вдоль линии ее действия, то моменты сил и результирующие силы не будут меняться, если мы имеем дело с абсолютно твердым телом. В этом случае не будут меняться и уравнения движения (2.11.1), (2.11.2).

Если найдены решения уравнений (2.11.1), (2.11.2), при известных начальных условиях, то определены и шесть координат, характеризующих движение твердого тела. Эти координаты являются функциями времени. Однако системы уравнений (2.11.1) и (2.11.2) не всегда позволяют получить решение в аналитической форме. В этом случае говорят, что уравнение движения не удается проинтегрировать, и решение уравнений находят путем численного интегрирования.