2.4. Момент сил

Моментом силы относительно некоторой оси называется произведение силы на ее плечо. Плечо силы — расстояние от линии действия силы до этой оси. Линия действия силы — линия, вдоль которой действует сила.

Пример 1. Возьмем доску и закрепим ее в некоторой точке О. Приложим к концу доски несколько сил (рис. 2.3).

Рис. 2.3. К определению момента сил, приложенных к телу

Прямая KN — линия действия силы . Перпендикуляр, опущенный из точкиО на прямую KN, есть плечо этой силы. Поэтому момент силы равен. Размерность момента силыЛиния действия силыпроходит через точкуО. Поэтому плечо этой силы равно нулю. Плечо силы равноВ общем случае величина момента силы равна

где — расстояние от оси до точки приложения силы, а— угол между радиус-вектором и направлением действия силы.

Из опыта следует, что тело может вращаться по часовой стрелке или против нее. Поэтому моменту силы приписывают определенное направление. Это направление определяется правилом правого винта.

Момент силы относительно оси, проходящей через точку О, есть вектор, перпендикулярный к плоскости, в которой лежат вектори радиус-вектор, равный по величине произведениюи направленный по правилу правого винта (буравчика)(рис. 2.4).

Рис. 2.4. К определению момента силы

Тогда, воспользовавшись определением векторного произведения, имеем:

. (2.4.1)

2.5. Момент количества движения материальной точки

Пусть имеется материальная точка массой , на которую действует сила . Уравнение движения точки имеет вид:

.

Умножим обе части этого уравнения векторно на радиус-вектор , в результате получим:

(2.5.1)

В правой части (3.5.1) мы получили выражение для момента силы относительно выбранной оси. Левую часть (3.5.1) преобразуем, используя правила векторного исчисления. Вычислим производную по времени от векторного произведения:

Учтем, что , и получим:

Моментом количества движения или моментом импульса отдельной частицы (материальной точки) относительно произвольно выбранной фиксированной точки (фиксированной в инерциальной системе отсчета) определяется соотношением (рис. 2.5):

. (2.5.2)

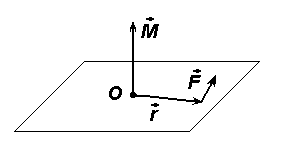
Рис. 2.5. К определению момента импульса материальной точки

Тогда выражение (2.5.2) примет вид:

(3.5.3)

Итак, скорость изменения момента импульса равна моменту сил. Это важное соотношение называется уравнением моментов.

2.6. Момент инерции материальной точки

Представим себе материальную точку, движущуюся по окружности радиуса . При вращательном движении линейнаяи угловаяскорости связаны соотношением:

Поэтому выражение для момента импульса в этом случае примет следующий вид:

(2.6.1)

Двойное векторное произведение (2.6.1) может быть представлено как

Окончательно получаем выражение для момента импульса материальной точки, вращающейся относительно некоторой оси:

(2.6.2)

Моментом инерции материальной точки называется физическая величина, равная произведению массы точки на квадрат расстояния от этой точки до некоторой оси:

(2.6.3)

Очевидно, что момент инерции точки будет разным относительно разных осей.

2.7. Момент количества движения системы материальных точек

Суммарный момент количества движения (момент импульса) системы частиц относительно произвольно выбранной точки (оси) в инерциальной системе отсчета будет равен

(2.7.1)

где  — масса  — той точки, — ее скорость в системе XOYZ. Положение точек системы показано на рис. 3.1.10.

Рис. 2.6. К определению момента количества движения системы материальных точек

Если вектор представляет собой вектор, характеризующий положение центра масс относительно начала отсчета, то это выражение можно записать в более удобном виде:

где  — момент импульса относительно центра масс и —полный импульс (или количество движения) частиц. Слагаемоепредставляет момент импульса центра масс относительно начала отсчета и зависит от выбора системы отсчета. Слагаемоене зависит от выбора начала отсчета.

Между частицами действуют внутренние силы. Примем без доказательства утверждение, что их суммарный момент равен нулю. Тогда уравнение изменения момента импульса принимает следующий вид:

(2.7.2)

Во многих случаях за начало отсчета удобно выбирать центр масс. В такой системе отсчета точки осуществляют вращение вокруг оси, проходящей через этот центр. В свою очередь, центр масс движется под действием результирующей силы. Вращение точек системы определяется результирующим моментом внешних сил.

Твердое тело, как мы уже отмечали, можно рассматривать как совокупность малых элементов с массой . Поэтому полученные результаты применимы и к рассмотрению вращательного движения твердого тела. Чтобы прояснить основную физическую идею этой главы и выявить основные трудности, рассмотрим следующие примеры.

Пример.Пусть имеется тонкий обруч радиусомR, например, велосипедное колесо. Приведем этот обруч во вращательное движение относительно оси проходящей через центр обруча и перпендикулярной его плоскости (рис. 2.7).

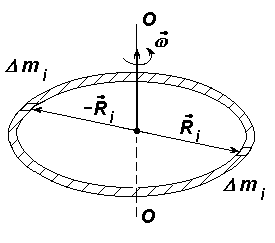
Рис. 2.7. Вращающийся обруч

В этом случае массы всех элементов находятся на одинаковом расстоянии от оси. Поэтому модуль момента импульса обруча равен

Здесь мы использовали тот факт, что все точки обруча движутся с одинаковыми по модулю скоростями, равными

По аналогии с вращением материальной точки величину назовеммоментом инерции обруча относительно оси, проходящей через центр масс и перпендикулярной плоскости обруча.

Докажем, что в данном примере имеет место следующее соотно- шение:

.

Вернемся к основному определению момента импульса, и поместим начало отсчета в центр масс тела. Тогда имеем:

Раскрывая двойное векторное произведение, получим:

(2.7.3)

Направление векторов исовпадают только в том случае, если второе слагаемое (2.7.3) равно нулю. Это возможно при выполнении одного из двух условий. Во-первых, если векторыивзаимно перпендикулярны, и, следовательно, скалярное произведение. В рассматриваемом примере это условие выполнено. Во-вторых, если тело является однородным и симметричным относительно оси вращения. В этом случае каждому элементунайдется соответствующий элементи при суммировании второе слагаемое (2.7.3) обратиться в нуль. В случае с обручем и это условие оказывается выполненным.

Следовательно, при выполнении одного из двух найденных условий уравнение вращательного движения твердого тела имеет следующий вид:

. (2.7.4)

Если отмеченные условия не выполняются, то описание вращательного движения становится сложным.

Для тела произвольной формы с произвольным распределением масс момент импульса уже не равен простому произведению скалярной величины на вектор. Именно это обстоятельство и является причиной сложного поведения вращающихся тел. Уравнение вращательного движения и в этом случае имеет вид:

. (2.7.5)