9.2. Регрессия

Наряду с корреляционным анализом проводится регрессионный анализ, который заключается в определении формы связи зависимой случайной величины y с независимыми случайными величинами X₁, X₂, …, X_n.

Форма связи результативного признака y с факторами X₁, X₂, …, X_n называется уравнением регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (квадратичную, экспоненциальную, логарифмическую и т. д.).

В зависимости от числа взаимосвязанных признаков различают парную и множественную регрессии. Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной, если между тремя и более признаками – множественной (многофакторной) регрессией.

Тест 9.5. Уравнение y = 5 + 0,2x₁ + 1,7x₂ определяет следующий вид регрессии:

1. множественный линейный;

2. множественный нелинейный;

3. парный линейный;

4. парный нелинейный.

При изучении регрессии следует придерживаться определенной последовательности этапов.

Этап 1. Установление формы зависимости. Пусть в результате наблюдений двумерной случайной величины (X;Y) получены данные, представляющие собой совокупность точек (x₁;y₁), (x₂;y₂), …, (x_n;y_n). Графическое изображение этих точек в плоскости Oxy представляет собой корреляционное поле (диаграмму рассеяния). Диаграмма рассеяния позволяет произвести визуальный анализ эмпирических данных и графически определить вид функции регрессии.

Тест 9.6. Результаты измерений признаков X и Y изображены в виде точек (x_i; y_j), на корреляционном поле в виде рис. 20.

Рис. 20

Тогда связь между признаками является:

1) линейной;

2) квадратической;

3) экспоненциальной ;

4) логарифмической;

5) кубической.

Тест 9.7. Результаты измерений признаков X и Y изображены в виде точек (x_i; y_j), на корреляционном поле в виде рис. 20. зависимость между признаками определяется уравнением:

1) y = ax + b;

2) y = ax² + bx + c;

3) y = ae^bx ;

4) y = alnx;

5) y = ax³ + bx² + cx + d.

Этап 2. Определение параметров (коэффициентов) уравнения регрессии.

Параметры уравнения регрессии определяются с помощью метода наименьших квадратов.

Этап 3. Проверка общего качества уравнения регрессии. Для определения величины степени стохастической взаимосвязи результативного признака и факторов необходимо знать следующие дисперсии:

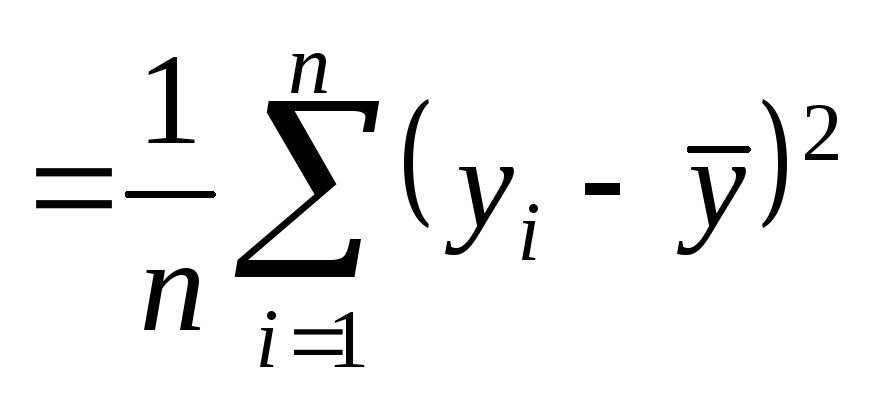• общую дисперсию результативного признака , отображающую влияние как основных, так и остаточных факторов: ,где – выборочное среднее значение результативного признакапо выборке;

• факторную дисперсию результативного признака , отображающую влияние только основных факторов: , гдезначения, найденные по уравнению регрессии;

• остаточную дисперсию результативного признака, отображающую влияние только остаточных факторов:

.

При корреляционной связи результативного признака и факторов выполняется соотношение: , при этом=+.

Для анализа общего качества уравнения линейной регрессии обычно используется множественный коэффициент детерминации R², называемый также квадратом коэффициента множественной корреляции. Множественный коэффициент детерминации рассчитывается по формуле =и определяет долю разброса результативного признака, обусловленную изменением факторных признаков, входящих в многофакторную модель. Чем теснее линейная связь между признаками, тем ближе коэффициент детерминации к единице. Однако, при достаточно близком к единице коэффициенте детерминации не всегда наблюдается тесная взаимосвязь между случайными величинами. Поэтому необходимы дополнительные исследования.

Этап 4. Проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов.

Проверяются соответствующие гипотезы