Глава 1.5 описание групп с помощью графов

Название этой главы входит в заголовок девятнадцатой главы второго издания книги Бернсайда «Теория групп конеч­ного порядка», вышедшего в 1911 г. С одной стороны, оно охва­тывает описание группы посредством покрытия сферы, евклидо­вой плоскости или неевклидовой плоскости копиями фундамен­тальной области этой группы, которая в таком случае должна ^*) действовать на заданном многообразии как дискретная группа преобразований. С другой стороны, то же название применяется: по отношению к одномерному комплексу, который может быть связан с тем или иным заданием группы. Такой комплекс на­зывается диаграммой Кэли, цветной группой, изображением группы (Gruppcnbild) или графом группы. Мы будем пользо­ваться последним термином.

Ясно, что покрытие двумерного многообразия копиями фун­даментальной области какой-либо группы, действующей на этом многообразии, непосредственно приводит к графу данной груп­пы. В самом деле, достаточно рассмотреть комплекс, двойствен­ный к тому, который возникает из покрытия. Именно так граф группы был введен Бернсайдом в [1911|. Впрочем, Бернсайд одновременно приводит и абстрактное определение, показываю­щее, что граф группы не зависит от наличия действия группы на двумерном многообразии. Прежде чем обсуждать важность самой идеи графа группы, дадим исторический обзор развития этого понятия и его применений. При этом мы не будем ка­саться большинства работ, рассматривающих только конечные группы. Хорошим источником информации об этом предмете мо­гут служить книги Бернсайда [1911] и Коксетера и Мозера [1965].

Кэли начинает свою статью [1878b] словами:

«Я приведу основы общей теории в тон мере, в которой это необходимо для понимания излагаемого мною квазигеометрического подхода.»

В этой статье, названной «К теории групп», Кэли приводит определение группы, строит таблицу умножения для группы А четных подстановок на множестве из четырех элементов и за­мечает, что использование 12 символов для 12 элементов группы излишне, можно обойтись двумя символами а, р. Остальные элементы группы могут быть выражены через эти:

1, а, а², р²ар², 0а², р²а, р², ра²ра², ра, р, р²о², Р²ар²а,

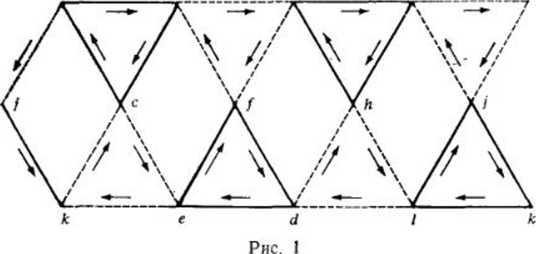
Далее, Кэли рассматривает пример того, что он называет hemihedron (полугранником). Это куб, «вершины» которого срезаны так, что получается многогранник с восемью треуголь­ными гранями и шестью квадратными, который затем пред­ставляется диаграммой, приведенной на рис. 1. Многогранник может быть получен из этой диаграммы отождествлением ре­бер, концы которых имеют одинаковые пометки а, /, к. Кэли продолжает:

«...диаграмма, линии которой, окрашенные в красный и черный цвета, так и будут называться красными и черными: при этом черные линии изобра­жены сплошными, а красные — пунктирными: каждая грань обозначает неко­торую циклическую перестановку в соответствии со стрелками. Первоначаль­ный рисунок содержал стрелки, но символы отсутствовали: затем, однако, я их ввел таким образом, что группа, задаваемая диаграммой в ее теперешнем виде, является в точности группой, содержащей упоминавшиеся выше подстановки

а = abc • de\ • ghi • jkl и 0 = ajg • bif • cek • Uhl

(a не другой группой, эквивалентной этой).

Заметьте, что на диаграмме, если учесть направление линий, задаваемое стрелками, из каждой точки выходит ровно одна черная линия и ровно одна красная...

Эга диаграмма обладает тем свойством, что всякий путь, ведущий нз какого-нибудь символа в него же, ведет также и из любого другого символа (лежащего на этом маршруте) в тот же самый символ.

....именно в силу этого свойства наша диаграмма задает группу.»

Далее Кэли изучает свой пример более подробно и заме­чает, что его конструкцию можно обобщить и что диаграммы

a b i g а

этого типа, удовлетворяющие определенным требованиям, при­водят к группам. Последнее показать нетрудно, и мы можем теперь процитировать определение, данное Бернсайдом в [1911, с. 424—425]:

«Предположим теперь, что задана диаграмма, состоящая из N точек, соединенных N{N—I)/2 окрашенными направленными линиями с соблюде­нием следующих условий:

1. произвольная линия любого цвета (а) имеет одну стрелку, указы­вающую ее направление, или (Ь) не имеет никакой стрелки, в этом случае линия считается эквивалентной двум совпадающим линиям, проведенным в противоположных направлениях;

2. имеется ровно одна линия любого цвета, ведущая в произвольную точку диаграммы, и ровно одна линия любого цвета, выходящая из всякой точки; линия, у которой стрелка отсутствует, обозначает две линии этого цвета, идущие в противоположных направлениях;

3. всякий путь, являющийся, если его начать с какой-нибудь точки диаграммы, замкнутым, т. е. ведущим в ту же точку, будет замкнутым, если его начать с любой другой точки.

Тогда, если эти условия выполнены, диаграмма является графическим изображением определенной группы порядка N*.

Далее Бернсайд [1911, с. 426] замечает, что мы можем вы­бросить все линии какого-нибудь одного цвета, если при этом диаграмма не потеряет связности, и в заключение пишет:

«Простейшая диаграмма, представляющая группу, должна содержать наименьшее число цветов и при этом связывать все точки... Можно заметить, что эта упрощенная диаграмма строится из полученного выше представле­ния группы пугем регулярного деления поверхности...»

Вместо бернсайдовского определения цветной группы нам хотелось бы воспользоваться определением Машке [1896], прак­тически совпадающим с бернсайдовским. И то, и другое яв­ляются непосредственной реализацией идей Кэли. В то же вре­мя нам хотелось бы подчеркнуть, что предложенное Дэном опре­деление изображения группы (Gruppenbild) основано на ином подходе. Кэли, Машке и Бернсайд исходили из того, что группа известна, и строили граф, который позволял затем выявлять порождающие и определяющие соотношения. Дэн в [1910] на­чинает с задания группы G с помощью конечного числа по­рождающих «у, v = 1, .... к, и конечного числа определяющих соотношений Si —1, .... S_m = 1 и затем описывает процедуру построения изображения группы. Мы приведем первый абзац этого построения:

«Мы строим следующий одномерный комплекс (Streckenkomplex) С°, ас­социированный с G:

Пусть

Si ^{в а}\^аХ ••• ^а\ (^ei = + ^{1 нли} -¹)-

Мы выбираем точку Z и окружность (замкнутую кривую) К} с / вершинами Z, Р_и ..., Pi-1 и помечаем ZP_X меткой + a_kl нли — a_ki, Р_}Р₂ — меткой 4- а*, или —а_кг и т. д. в зависимости от значений -fl или —1 чисел е_:, ег, ...- Затем мы берем вторую окружность К², дуги которой, проходимые в данном направлении, начиная с Z, должны получить метки +а* или — а_кл, ...

.... + a_k или — о* , а_к нли — я*.. (Знаки опять выбираются в соответствии

со знаками е<) Мы продолжаем таким образом до тех пор, пока не исчерпаем все циклические перестановки мономов, входящих в Si. В результате мы полу­чим I окружностей, проходящих через Z, дуги которых при заданной ориен­тации получили описанные выше метки. Если мы обратим ориентацию, то знаки меток на дугах изменятся на противоположные. Пусть теперь имеются две дуги ZP и ZQ, имеющие (если считать Z начальной точкой) одну и туже метку. Тогда мы отождествляем Р и Q, равно как и дуги ZP и ZQ, и про­должаем этот процесс до тех пор, пока все метки на дугах, выходящих из Z, не станут различными. Мы будем проделывать то же самое для всех точек на всех наших окружностях до тех пор, пока метки на дугах, выходящих из любой фиксированной точки, не станут различными. Обозначим получен­ный комплекс через С³ и назовем Z его центром.»

Описанное построение проделывается для всех определяю­щих соотношений группы G. Хотя, вообще говоря (например, для бесконечных групп), это построение может потребовать бес­конечного числа шагов, Дэн отмечает, что должно быть верным следующее. Рассмотрим две различные точки Р и Q, полученные в результате г₀ шагов построения. Если Р и Q все еще разли­чаются после г > г₀ шагов построения при достаточно боль­шом г, то они будут различаться и после s г шагов при сколь угодно больших s. Дэн также замечает, что он лишь доказал существование изображения группы, но не дал метода его по­строения за конечное число шагов. Он указывает, что построе­ние изображения группы дает возможность решать проблему распознавания равенства для группы G. (Очевидно, что эти две проблемы совпадают, но Дэн этого не отмечает.)

Наконец, Дэн в (1910) приводит изображение графа конеч­ной группы с порождающими aj, аг и определяющими соотно­шениями

а* = 1, а*=1, a_la₂a_l^a₂= 1

и замечает в подстрочном примечании:

«Связь группы икосаэдра с этим комплексом известна. (См. Maschke, Am. Journ., 1896.) В целом понятие «изображения группы» не дает ничего суще­ственно нового в случае конечных групп. Оно тесно связано с цветной диа­граммой Кэли.»

Трудно понять, как Дэн не заметил, что его изображение группы совпадает с цветной диаграммой Кэли, причем не только для конечных групп. Впрочем, верно, что идея Кэли до Дэна применялась в основном к конечным группам, где она ведет к определению рода группы как наименьшего рода замкнутого ориентированного двумерного многообразия, на котором можно нарисовать граф этой группы так, чтобы ребра не пересекались нигде, кроме вершин.

Прежде чем обсуждать, как Дэн использовал граф группы, мы коротко упомянем о воздействии этого понятия на теорию конечных групп. Безусловно, идея графа группы выглядела изящной и привлекательной. В книге Бернсайда [1911] цветная группа (для группы октаэдра или 2₄) была помещена на фрон­тиспис. Дж. А. Миллер, который практически во всех своих 359 статьях, перепечатанных в собрании его сочинений, зани­мался только конечными группами, еще в 1935 г. писал:

«Эти диаграммы полезны для иллюстративных целей, но, видимо, до на­стоящего времени не привели к каким-либо новым теоремам в теории групп.»

По-видимому (если не касаться бесконечных групп, кото­рыми не интересовался и о которых не так уж много знал Миллер), это верно и по сей день (1980 г.). Надежда получить новую интересную классификацию конечных групп в соответ­ствии с их родом не сбылась. Можно отметить все же важность для теории уравнений седьмой степени с группой Галуа G.₆₈ того факта, что простая группа С_1б8 порядка 168 имеет род 3. Теорию этих уравнений нельзя построить аналогично теории уравнений пятой степени с группой Галуа А₅ из-за того, что автоморфные функции на римановой поверхности положитель­ного рода не являются рациональными функциями какой-либо одной автоморфной функции, см. Фрике [1926, с. 211—240].

Однако этот результат слишком специален для того, чтобы иметь существенный вес в наших рассмотрениях.

Возвращаясь к Дэну, можно отметить, что использование графов бесконечных групп оказалось весьма существенным для развития теории таких групп. Начнем с работы Дэна [1910], где мы находим построение графа группы узла-трилистника. Эта группа задается четырьмя порождающими Cj_f С₂, С₃, С_А и соотношениями

С,С,“ ‘С₂ = С2С4 'Сз = С3С4 'Cl = 1.

Дэн не указывает своего способа построения, а приводит окончательный результат, который оказывается неожиданно простым и выглядит, по крайней мере с интуитивной точки зрения, весьма убедительным. То, что эта группа не абелева, становится очевидным, и вся информация о ней, которая потре­бовалась Дэну в его статьях [1910] и [1914], может быть получена из этого графа. Следует отметить, что центр группы три­листника является бесконечной циклической группой, а фактор­группа по центру — это хорошо известная модулярная группа PSL(2, Z), задаваемая двумя порождающими а, b и соотноше­ниями а² = 6³ = 1. Дэн мог бы воспользоваться этим фактом для построения графа. Действительно, граф модулярной группы может быть легко извлечен из хорошо известного покрытия не­евклидовой плоскости фундаментальными областями этой груп­пы. Однако конструкция Дэна является прямой и весьма про­стой. В подстрочном примечании в [1914] он также замечает, что его аспирант построил «интересный групповой граф» для группы узла восьмерки (узла Листинга). Все, что мы знаем (из устной информации) по данному поводу, — это имя аспи­ранта: Фриц Клейн. Очень вероятно, что он, как и другой аспи­рант Дэна Гизекинг, погиб в первой мировой войне, унесшей много молодежи (в частности, научной молодежи) Европы.

В [1911] Дэн предваряет главу о фундаментальных группах замкнутых поверхностей следующими замечаниями:

«Нельзя сказать, что в случае фундаментальных групп замкнутых поверх­ностей чистая теория групп может оказать существенную помощь топологии. Напротив, решение топологических проблем стимулирует исследования в тео­рии группа

В своей статье Дэн изучает проблему распознавания ра­венства и сопряженности для фундаментальных групп замкну­тых двумерных многообразий. При этом он использует покры­тия неевклидовой плоскости фундаментальными областями дис­кретной группы преобразований Мёбиуса; эти преобразования дают точное представление для фундаментальных групп. Хотя существование таких представлений было известно уже в те­чение определенного времени (и содержится, например, в фун­даментальном труде Фрике и Клейна [1897]), для них не было известно никаких явных формул. Отыскание соответствующих формул составило содержание первой главы диссертации Ги- зекинга — аспиранта Дэна. Диссертация появилась в 1912 г., и Дэн в [1912] ссылается на нее. В то же время он замечает, что неевклидова геометрия совсем не нужна для решения про­блем распознавания равенства и сопряженности для этих групп. Все, что ему нужно, — это топологические свойства графа груп­пы (который просто двойствен покрытию неевклидовой плоско­сти неевклидовыми многоугольниками). Упомянутые свойства состоят в следующем: граф состоит из 4^-угольников (g> 1) и в каждой вершине сходится ровно 4g из них. В [1912] Дэн заметил, что это условие можно ослабить: достаточно предпо­лагать, что граф составлен из многоугольников с числом вершин нс менее семи и в каждой вершине сходится не менее четырех из этих многоугольников. При этом молчаливо подразумевается, что никакие два многоугольника не могут иметь более одной общей стороны. Как показывает работа Гриндлингсра [!960Ь], число 7 является в некотором смысле оптимальным.

Независимо от частных результатов, полученных Дэном с использованием его «изображений групп», остается вопрос, мо­жет ли введенное Кэли графическое представление служить ка­ким-нибудь другим целям, кроме, по выражению Миллера из

1935. , «иллюстративных». В конце концов результаты Дэна можно получить алгебраически, и в более сложных случаях, чем те, которые изучал Дэн, алгебраические методы оказываются более простыми, поскольку описание графа конкретной группы может стать безнадежным делом. Уже в случае группы узла Листинга (узел восьмерки) никто даже не пытался воспроиз­вести граф группы, найденный аспирантом Дэна Фрицем Клей­ном. Алгебраически же нетрудно доказать, что эта группа яв­ляется бесконечным циклическим расширением свободной груп­пы ранга 2, а это позволяет непосредственно вычислить ее группу автоморфизмов (см. Магнус [1931]). Времена интуи­тивного использования топологии прошли. Дэн любил повто­рять, что он всегда знал результат из работы Шрейера [1927а] о том, что подгруппа свободной группы свободна, так как «в конечном итоге подграфы дерева — это деревья». Но строгий вывод соответствующего топологического утверждения и извле­чение из него теоретико-группового требует определенной рабо­ты, а с другой стороны, и шрейерово алгебраическое доказа­тельство не очень сложно.

Вопреки всем соображениям такого сорта мы полагаем, что Дэн был прав. Он был прав не только в том общем смысле, что, как он отметил, топологические задачи (и, мы можем до­бавить, понятия) стимулируют исследования в теории групп. Уверенность Дэна в важности «изображений групп», особенно подчеркиваемая в устных обсуждениях, основывалась на глу­боком внутреннем осознании того факта, что графическое зада­ние группы является адекватным выражением определенной стороны ее природы. Графы использовались в комбинаторной теории групп, по крайней мере эпизодически, начиная с момен­та, когда они были введены в работе Дэна [1910], да и сама работа Шрсйсра [1927а], о которой говорил Дэн, содержит интересное расширение конструкции Дэна — граф смежных классов по подгруппе. Но наиболее впечатляющим подтвержде­нием оценки Дэна, вероятно, является работа Столлингса [1968]. Основная се теорема гласит: «Конечно заданная группа без кручения, имеющая конечное число концов, является сво­бодным произведением двух нетривиальных сомножителей». Число концов группы определяется следующим образом (см. Хопф [1944]). Удалим конечное число ребер из графа группы. Подсчитаем число бесконечных компонент связности получив­шегося графа. Точная верхняя грань N числа таких компонент при числе удаляемых ребер, стремящемся к бесконечности, на­зывается числом концов группы. N может принимать только три значения: 1, 2 или оо.

Следует обратить внимание на то, что данное определение является чрезвычайно простым в топологических терминах, в то время как любой перевод его в алгебраические термины ока­зывается неуклюжим и запутанным. Конечно, можно сказать, что все это связано с необходимостью уточнения определения. Дэн, безусловно, так не считал. В своем публичном выступлении перед учеными-нематематиками [1928] он утверждал, что про­должающийся рост математического знания требует появления новых идей, которые позволят достичь дальнейших упрощений. Он также выражал надежду, что топология должна обновить свои силы в результате такого привлечения новых идей. Следует обратить внимание на год, когда это было сказано. В течение последующих десяти лет появились монографии по топологии Александрова и Хопфа, Лефшеца, Зейферта и Трельфалля, за­фиксировавшие расцвет топологических исследований, продол­жающийся по сой день.