§4.Приложения кратных интегралов.

1˚. Геометрические приложения.

1. Площадь плоской фигуры.

Пример. Найти площадь фигуры, ограниченной линиями:,,.

Решение.

Для того, чтобы не пришлось разбивать область , перейдём к новым координатам так, чтобы граничные кривые оказались координатными линиями новой криволинейной системы. Именно, пусть, а еще лучше. Тогда будет. При этом в областибудет, а,

. Поэтому .

2. Объем тела может быть найден по формулам: , где − проекция телана плоскость.

Пример. Доказать, что объем шарового сектора пропорционален “стрелке” соответствующего сегмента (при фиксированном радиусе).

Решение. Проще всего воспользоваться сферическими координатами. В этом случаеи .

3. Площадь искривленной поверхности.

Предположим, что поверхность задана явным уравнением, где, а− квадрируемая область, представляющая собой проекциюна плоскость.

Разобьём на квадрируемые подмножестваи выберём в них по точке. Обозначимточку на поверхности, проецирующуюся. Рассмотрим касательную плоскостьв точкеи обозначимплощадь части этой плоскости, проецирующейся.

Так как площадь , где− угол между касательной плоскостью и плоскостью, то. Действительно, величина равна третьему направляющему косинусу нормального векторак поверхностив точке, лежащей над точкой.

Определение. Рассмотрим площадь “описанного многогранника”.

Если существует предел суммыпри условии, что мелкость разбиениястремится к нулю, будем считать этот предел площадью поверхности. Ясно, что.

Пример. Найти площадьчасти параболоида вращения, отсекаемой плоскостью.

Решение. =.

Рассмотрим случай параметрического задания поверхности с помощью уравнения,. Мы будем называтькриволинейными координатами на поверхности. Эти координаты называютсяортогональными, если в каждой точке.

Рассмотрим криволинейный “параллелограмм”, заключённый между двумя парами бесконечно близких координатных линий и линий. С точностью до главных бесконечно малых его площадь равна. Поэтому, где− область изменения параметров.

Ясно, что . Поэтому

.

Рассмотрим матрицу Грама для векторов. Это значит,,. Так как, то. Поэтому

.

В частности, если криволинейные координаты на поверхности ортогональные, то и

.

Так, если − широта и долгота точки, то,, В этом случае площадь фигурына сферебудет равна, где− область изменения координат.

2˚. Физические приложения кратных интегралов.

Массу тела можно найти по формуле, гдеобъёмная плотность материала, массу пластины − по формуле(на этот раз− поверхностная плотность). Точно так же, зарядможно вычислить, интегрируя объёмную (поверхностную) плотность распределения заряда.

Центр масс: , здесь− снова масса тела.

Моменты инерции: ,,и т.д.

Напряженность в точке гравитационного поля, создаваемого массой, распределённой с плотностью, равна, где− гравитационная постоянная. Потенциал гравитационного поля равен.

Аналогичные формулы справедливы, но со знаком “минус” и для напряженности и потенциала электростатического поля.

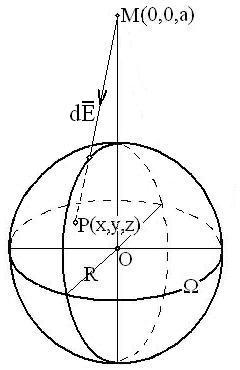
Пример. Доказать, что однородный шар притягивает материальную точку так, как если бы вся масса шара была сосредоточена в его центре.

Решение. Если расположить шар и точкутак, как показано на рисунке, будет. Вычислим, считая, что.

. Сделаем во внутреннем интеграле следующую замену:. При этом будет,;. , где− масса шара.