Глава 5.Неопределенный интеграл. §1. Основные определения.
Определение 1.
Функция
называется первообразной функцией
на интервале
,
если
при всех значениях
.
Замечание. Дальше будет доказано, чтоу непрерывнойфункцииесть первообразная.
Определение 2. Множество всех
первообразных
на некотором интервале называетсянеопределенным интеграломэтой
функции и обозначается
(название “интеграл” и данное обозначение
будут объяснены позже).
Лемма. Различные первообразные одной и той же функции отличаются друг от друга на постоянное слагаемое.
Доказательство. Пусть
и
первообразные функции
на интервале
и пусть
.
Докажем, что
на этом интервале, иначе говоря, что для
любых двух значений
будет
.
Действительно, так как
,
то, согласно теореме Лагранжа, существует
число
,
заключенное между числами
и
,
такое что
.
А так как
,
то
.
Следствие.Если
− какая-либо первообразная функция
,
то
,
где
− произвольная постоянная.
Простейшие свойства неопределенного интеграла.
1.
,
но
,.
2.
(свойство линейности интеграла).
Замечание 2. Операция интегрированиявыводитиз класса элементарных
функций. Примерынеэлементарныхинтегралов от элементарных функций:
,
,
и др. Доказательство неэлементарности
некоторых интегралов первыми дали
Лиувилль и Чебышев.
Нам будет необходима таблица неопределенных интегралов. В простейших случаях табличные интегралы получаются непосредственно из табличных производных, так как интегрирование − действие обратное дифференцированию. В более сложных случаях нам придется наметить пока только левые части табличных соотношений, а окончательное оформление отложить ненадолго.
Заметим, однако, что техника интегрирования, в отличие от техники дифференцирования не сводится к использованию таблицы и нескольких правил. Она в большой степениявляетсяискусством.
§2. Таблица основных неопределенных интегралов.
1.
.
2.
.
3.
.
4*.
5.
5’.
.
6.
.6’.
.
7.
.7’.
.
8.
.8’.
9.
.9’.
.
10*.
11*.
12.
.
13.
.
14.
.
15.
.
16*.
17*.
§3. Замена переменной в неопределенном интеграле.
Теорема. Пусть
− функция класса
,
а
обладает первообразной функцией
на интервале
.
Тогда
1.
.
Если, кроме того,
производная
сохраняет знак на интервале
,
то
2.
,
где
− функция, обратная по отношению
.
Доказательство. 1. Правило дифференцирования сложной функции даёт:
.
2. Так
как производная
сохраняет знак, то замена
монотонная. Поэтому существует обратная
функция
,
непрерывная на интервале
.
Если подставить в уже доказанное
соотношение 1.
,
то получим
.
Ч. и т. д.
Вычислить
интегралы:
,
,
,
.
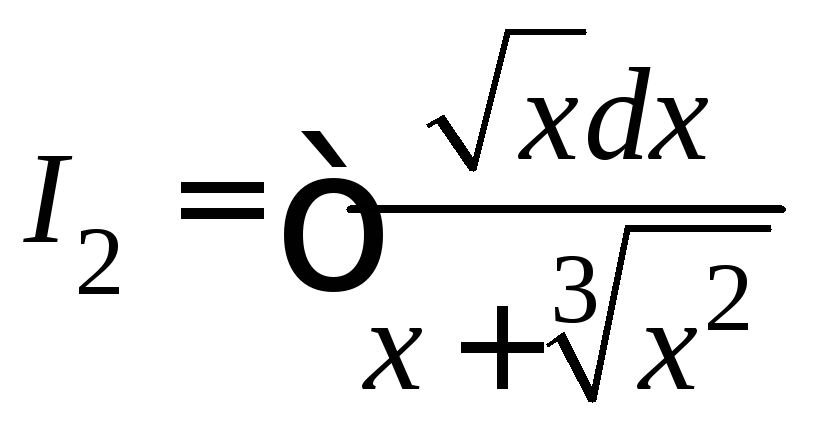Решение. 1. Пусть
.
Тогда
,
т.е.
.
Следовательно,
.
2.Делаем замену:
или
.
При этом
,
,
.
Поэтому
.
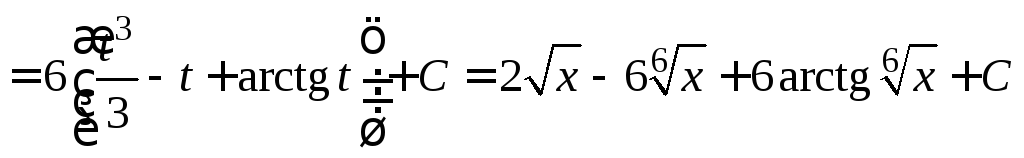3.
.
Это − табличный
интеграл 10*.
.
Из него сразу следует еще одна табличная
формула: 11*.
.
4. Сделаем
замену (монотонную)
,
или
.
Тогда будет
и
.
Поэтому
=
.
Это приводит нас к формуле16*.
.
§4. Интегрирование по частям.
1˚.Хорошо известна формула
.
К сожалению, нет подобного правила для
интегрирования произведения. Некоторой
компенсацией можно считать так называемоеправило интегрирования по частям:
или более кратко:
.
Теорема. Пусть на интервале
функции
и
дифференцируемы, а произведение
имеет первообразную функцию. Тогда
существует первообразная функция и у
произведения
,
причем справедлива формула
.
Доказательство.
.
Примеры.
Вычислить интегралы:
,
,
,
.
(Заметим, что
− табличный интеграл 4*.)
Решение. 1.
,
.
2.
.
3. 
.
4. 
.
5. Если,
например,
,
то
.
Полагаем снова
при этом
.
Поэтому
,
следовательно
.
2˚. Нам понадобятся рекуррентные формулы для вычисления интегралов вида
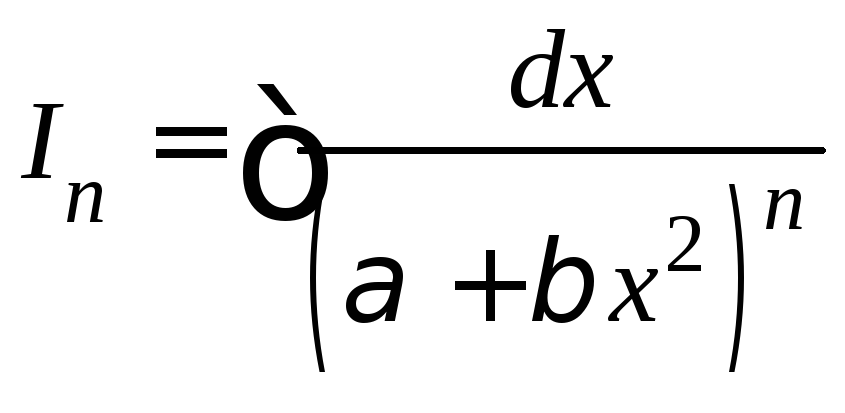и
.
Обозначим
.
Так как
,
то
,
следовательно,
.
Это даёт
.
Заменяя здесь
,
получим
.
Примеры. 1.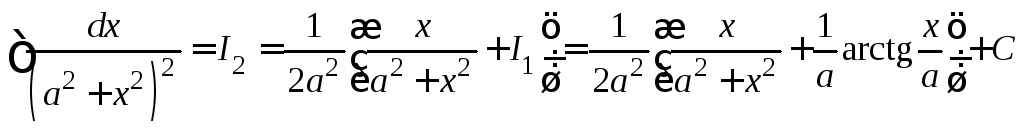 
.
(
)
2. 
.
(
)
Последнее равенство представляет собой табличную формулу 17*.
3˚. Таблица основных неопределенных интегралов.
1.
.
2.
.
3.
.
4*.
.
5.
5’.
.
6.
.6’.
.
7.
.7’.
.
8.
.8’.
9.
.9’.
.
10*.
.
11*.
.
12.
.
13.
.
14.
.
15.
.
16*.
.
17*.
.