§5. Алгебраические многочлены и дробно-рациональ­ные функции.

1˚. Комплексные числа.

Мнимая единица− это(imaginary). Так как, тоне может быть действительным числом.Комплексным числомназывается сумма вида, где. Числоназываетсядействительной частью, числоназываетсямнимой частью .Записывается это так:. Множество (поле) всех комплексных чисел обозначают.

Поставим в соответствие комплексному числу точку с декартовыми координатами. Полярные координаты этой же точки обозначим. В таком случае. Поэтому. Ясно, что. В отличие от алгебраическойзаписи, равенствоназываетсятригонометрической записью комплексного числа. Числоназываютмодулем, число−аргументом; их обозначения:.

Число называютсопряженным к числу. Ясно, что. Если,, то. Перемножать комплексные числа удобнее, если использовать их тригонометрическую запись. Действительно,

.

Таким образом, при перемножении комплексных чисел их модули перемножаются, а их аргументы складываются. Это подсказывает еще одну форму записи комплексных чисел − показательнуюилиэкспоненциальную: . Более естественное обоснование формул Эйлера

,

связывающих показательную функцию и тригонометрические функции, будет дано в теории степенных рядов.

Отметим свойства операции сопряжения: ,,.

2˚. Алгебраические многочлены. Мы будем рассматривать алгебраические многочлены, зависящие от комплексной переменной, с комплексными коэффициентами.

Теорема Гаусса(илиосновная теорема алгебры). Алгебраический многочленстепениимеет ровно(комплексных) корней с учетом их кратности.

Это означает, что существует разложение . Здесь− корни многочлена, а натуральные числа−кратностиэтих корней. Ясно, что.

Следствие 1. Пусть известно, что все коэффициенты многочлена−действительныечисла. В таком случае, если числоявляется корнемкратности, тотакже −корень этого многочлена.

Доказательство*. Имеем, так как− действительные числа. Следовательно,

.

Следствие 2. Многочлен с действительными коэффициентами разлагается на линейные и квадратичные множители с действительными коэффициентами.

Это вытекает из того, что .

3˚. Дробно-рациональные функции. Рациональной дробью называется отношение двух алгебраических многочленов. Рациональная дробь называетсяправильной, если степень числителя меньше степени знаменателя. В противном случае дробь −неправильная. Деля числитель дроби на знаменатель, можно превратить неправильную дробь в сумму многочлена и правильной дроби. Поэтому, для того, чтобы суметь проинтегрировать любую рациональную функцию нужно научиться интегрировать правильные дроби. Для этого нам потребуется умение разбить правильную дробь на простые дроби и умение интегрировать простые дроби. Начнем с определения.

Определение. Дробь называетсяпростой, если её знаменатель представляет собой линейную или квадратичную скобку в натуральной степени, а степень числителя на единицу, меньше чем степень многочлена, стоящего внутри этой скобки.

Теорема. Правильная дробьс действительными коэффициентами единственным способом может быть представлена в виде суммы простых дробей. Здесь каждой скобке в разложении знаменателя отвечает группа простых дробей, содержащих в знаменателях эту скобку в степенях от первой до той, с которой скобка входит в разложение знаменателе исходной дроби.

Пусть, например, . Тогда знаменатель можно разложить на множители минимальной степени=. Поэтомуразбивается на простые дроби следующим образом: .Для нахождения значенийобычно используютметод неопределенных коэффициентов. Мы обсудим этот прием при рассмотрении последующих примеров.

Доказательство теоремы*легко получить с помощью следующих двух лемм.

Лемма 1. Пусть− многочлены с действительными коэффициентами,− действительное число, причеми. Существует единственное действительное числои многочлен с действительными коэффициентамитакие, что выполняется тождество

.

Доказательство леммы 1. Рассмотрим разность

.

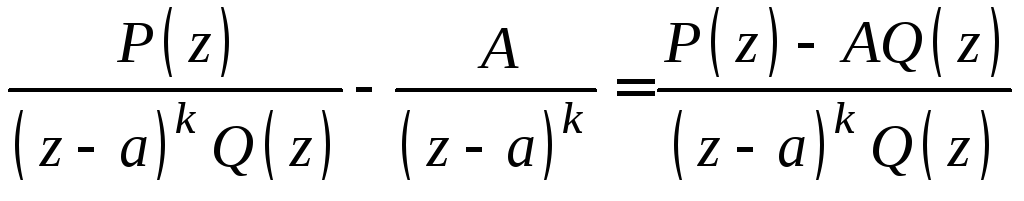Многочлен делится на двучлентогда и только тогда, когда, т.е., так как.

Лемма 2. Пусть− многочлены с действительными коэффициентами,− комплексное число,. Пусть еще известно, что(иначе говоря,не делится) и что. Тогда существует единственная пара действительных чисели многочлен с действительными коэффициентами, такие что

.

Доказательство леммы 2. Рассмотрим разность

.

Числитель последней дроби делится на квадратный трехчлен тогда и только тогда, когдаили. Последнее отношение определено, так как. Запишем это отношение в виде. Тогда для нахождения чиселполучим линейную систему с действительными коэффициентами:. Эта система имеет единственное (действительное) решение, так её определительпо условию отличен от нуля.