§6. Интегрирование дробей.

1˚. Интегрирование простых дробей.

Простые дроби подразделяются на четыре типа:

1. ;2. ;3.,4..

Здесь − квадратный трехчлен, не имеющий действительных корней.

Переходим к их интегрированию.

1..

2. .

3., где,,

(, так как квадратный трехчленне имеет действительных корней). Поэтому.

4. После той же замены, что и в случае 3, получим . При этом; а интегралможно вычислить с помощью понижения порядкапо рекуррентной формуле из §4.

1˚. Примеры интегрирования дробно-рациональных выражений.

1.Вычислить неопределенный интеграл, где.

Решение. Прежде всего.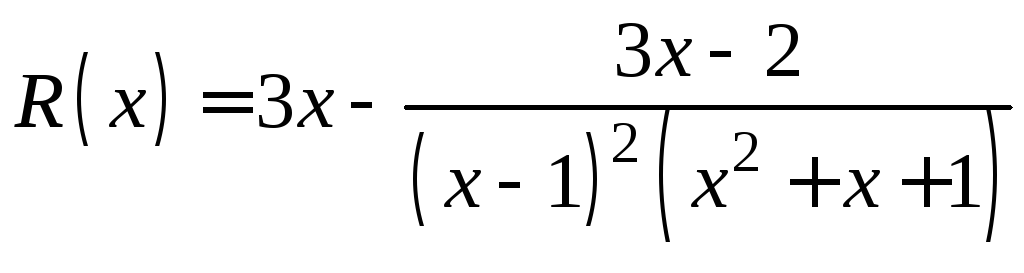

Разбиваем второе слагаемое на простые дроби:

.

Для отыскания чисел применяем метод неопределенных коэффициентов:

.

Приравнивая коэффициенты при одинаковых степенях в обеих частях этого равенства, получаем систему линейных уравнений:

. Отсюда следует, что. Поэтому

.

Окончательно получаем .

2.Вычислить неопределенный интеграл.

Снова . Поэтому

.

Применяя ко второму слагаемому рекуррентную формулу при , получаем

или

.

После упрощения получаем .

§7. Интегрирование выражений, рационально зависящих от функций .

1˚. Интегралы вида, где− дробно-рациональная функция, приводятся к интегралам от рациональных дробей (рационализуются) при помощи так называемойуниверсальной тригонометрической подстановки .Действительно, в этом случае,,. Поэтому

.

2˚. В некоторых частных случаях бывает удобнее пользоваться менее универсальными, но более простыми подстановками для рационализации подынтегрального выражения.

• Если зависитнечетно, т.е., где− рациональная функция, целесообразно сделать замену, так как

.

• Точно так же, если нечетно зависит, можно положить.

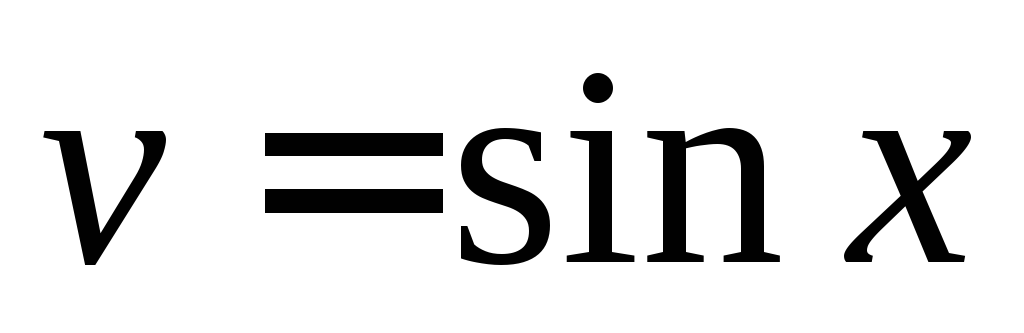• Если функция четна относительно совокупности переменных, точнее,, то удобно воспользоваться заменойили.

Пример1. . Вычислить интеграл.

1-й способ. Полагая , приходим к интегралу от рациональной дроби:. Попробуем применить более простую подстановку.

2-й способ. Так как здесь, можно принять. Тогда получим. Это уже лучше!

3-й способ. Обозначим знаменатель и представимв виде. Так как, то будет, и мы приходим к системе уравнений:, откуда следует, что. Поэтому.

Пример2. Вычислить интеграл.

Так как входит в нечетной степени, то полагаем ,тогда будет и потому

=.

Пример3. Вычислить интеграл. Здесь обе функцииивходят в четных степенях. Придется понижать степень обеих этих функций.

=.

Пример4. Вычислить интеграл.

Формулы Эйлера дают:

.

Поэтому .

В теории рядов Фурье часто приходится вычислять интегралы вроде следующего.

Пример 5. Вычислить интеграл.

Имеем .

§8. Интегрирование некоторых выражений, содержащих радикалы.

1˚. Интеграл от дробно-линейных (линейных) иррациональностей− это интеграл вида. Здесь− рациональная функция,, а все− натуральные числа. Для рационализации таких интегралов используется подстановка, где.

Пример 1. Вычислить интеграл.

Так как , полагаем. Это даёт,,.=.

Пример 2. . Вычислить интеграл.

Данный интеграл можно представить в виде . Поэтому целесообразно сделать замену. Тогда получим,,. Поэтому.

2˚. Интегрирование квадратичных иррациональностей.

1.Для вычисления интегралов вида, где− рациональная функция двух переменных, можно использоватьподстановки Эйлера.

I

II.Тогда будетили

, следовательно,и т.д.

IIIЕсли дискриминантквадратного трёхчленабольше нуля, то трёхчлен можно разложить на линейные множители:. В этом случае применима третья подстановка Эйлера:или(см. пункт 1˚).

Отметим, что в случае, когда , будети можно использовать любую из первых двух подстановки.

2. Интегралы от квадратичных иррациональностей можно привести к виду, где− рациональная функция одной переменной. Дробьможно представить в виде суммы алгебраического многочлена и простых дробей. Поэтому задача интегрирования сводится к вычислению подобных интегралов с заменойна алгебраический многочлен или простую дробь.

В первом случае удобно использовать следующий приём.

Метод Остроградского:

.

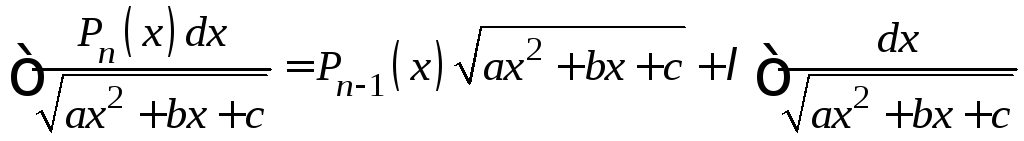Здесь − алгебраические многочленыстепени, соответственно. Коэффициенты многочленаи числоподбирают с помощью метода неопределённых коэффициентов.

Для вычисления интегралов 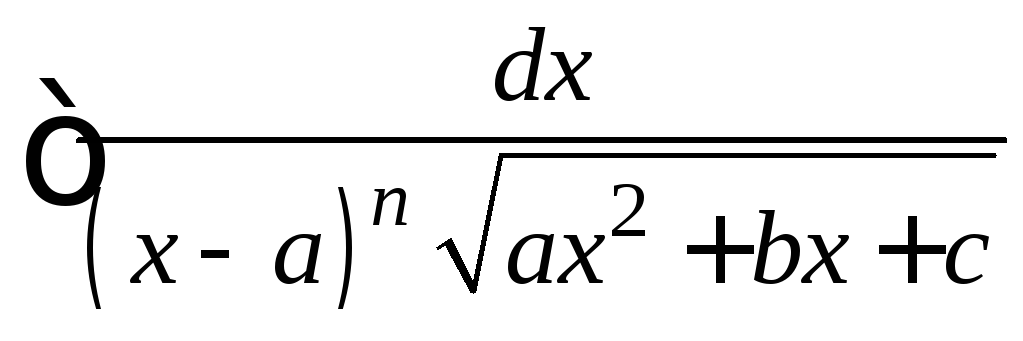можно использовать подстановку. Оставшиеся интегралы приводятся к виду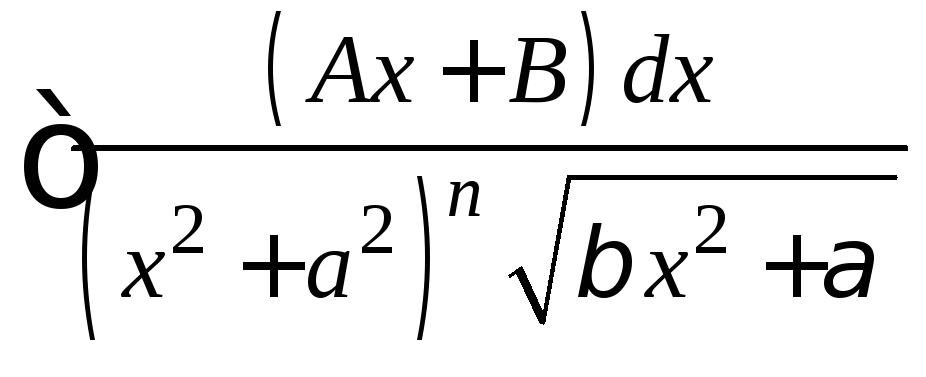, а к этому интегралу можно применитьподстановку Абеля.

Пример 3. Вычислить интеграл.

1-й способ.Подстановка Эйлера. Она приводит к сложным выкладкам.

2-й способ.. Дифференцируя это соотношение и домножая затем, приходим к равенству. Это приводит к системе линейных уравнений

. Решая систему, находим .Следовательно,

.

3-й способ.. После этой подстановки получаем

.

Другие способы. Для вычисления интеграламожно также воспользоваться подстановками.

Пример 4. Вычислить интеграл.

Прежде всего, . Для вычисления интеграладелаем замену. Тогда будет

,,или.

Поэтому

.