Глава 8. Ряды. §1. Основные определения. Свойства сходящихся рядов.

1˚. Теория бесконечных числовых рядов имеет много общего с теорией несобственных интегралов с бесконечным верхним пределом.

Определение 1. Рассмотрим бесконечный ряд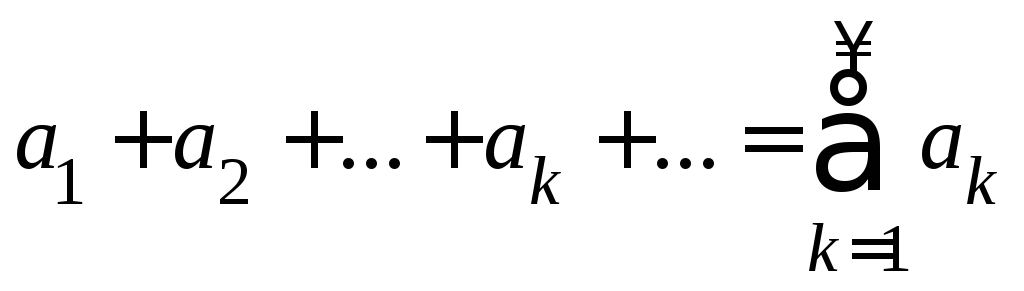. Егочастичнойсуммойназывается суммапервых членов данного ряда, то есть. Рядназывается остаточнымрядом.

Определение 2. Если существует конечный пределчастичной суммы, то этот предел называетсясуммойряда, а сам ряд считаетсясходящимся. В противном случае говорят, что рядрасходится.Сумма остаточного ряда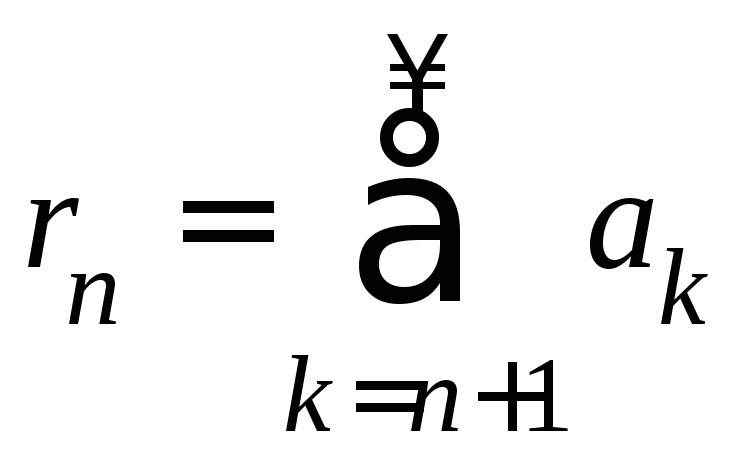называется остаткомряда.

Предложение 1. Если рядсходится, то сходится любой из его остаточных рядов. При этом.

Доказательство. Так как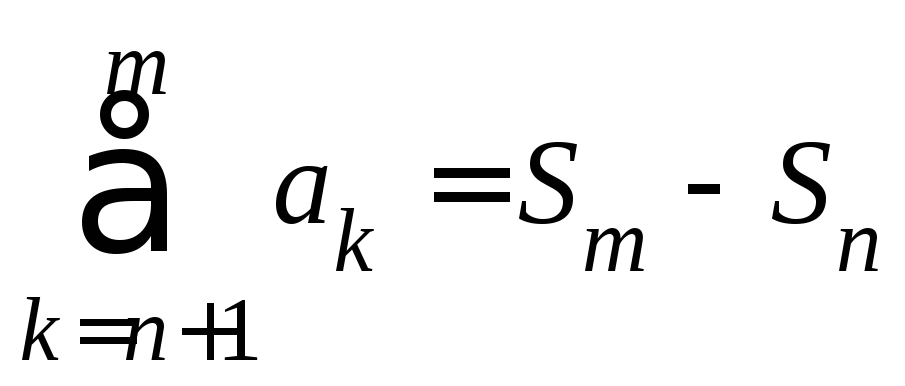, то нужно лишь перейти к пределу при условии, что.

Предложение 2. (Критерий Коши для рядов). Для сходимости ряданеобходимо и достаточно, чтобы его усечённый остаток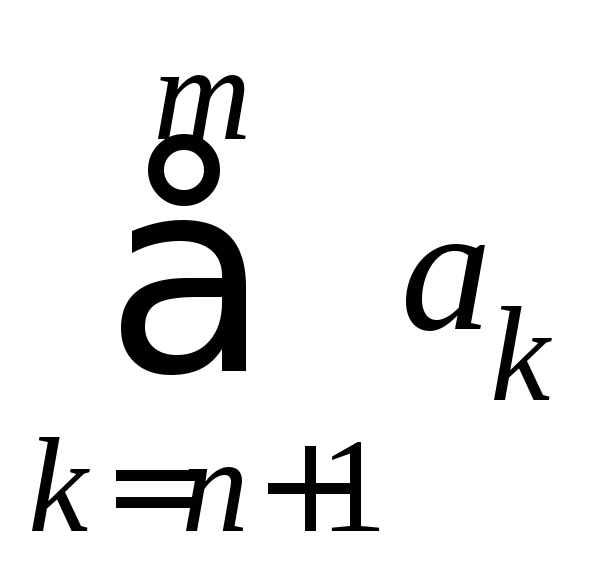стремился к нулю, когда(условие Коши).

Доказательство. Так как,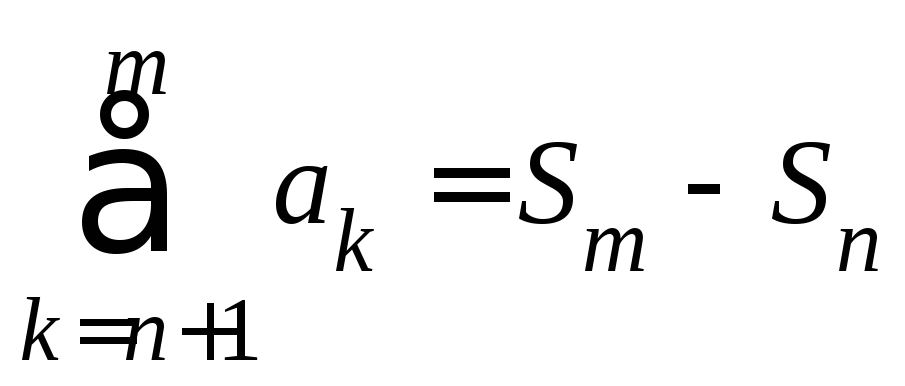, то остаётся применить критерий существования конечного предела к последовательности.

Предложение 3. (Необходимое условие сходимости). Если рядсходится, то. Обратное утверждение не верно.

Доказательство. Необходимость условия является следствием критерия Коши. Для того, чтобы убедиться в его недостаточности, рассмотрим гармонический ряд:. Ясно, что. В то же время. Так как нарушено условие Коши, то ряд расходится.

2˚. Свойства сходящихся рядов.

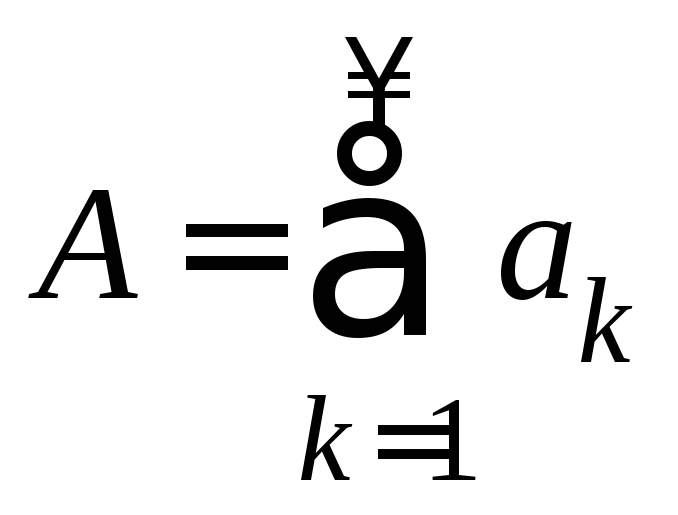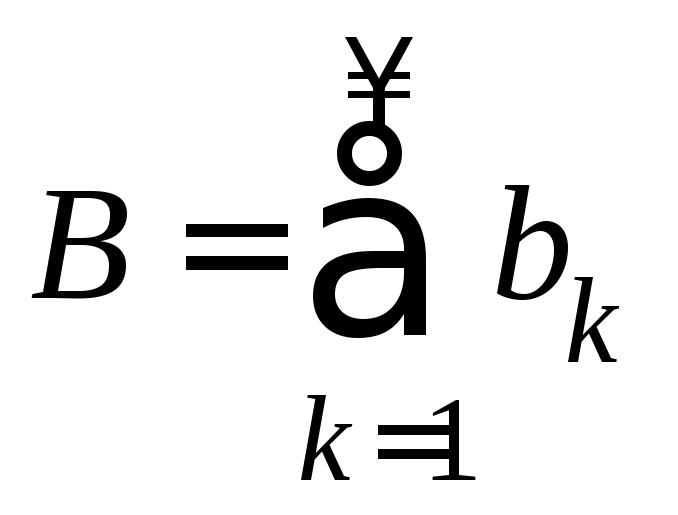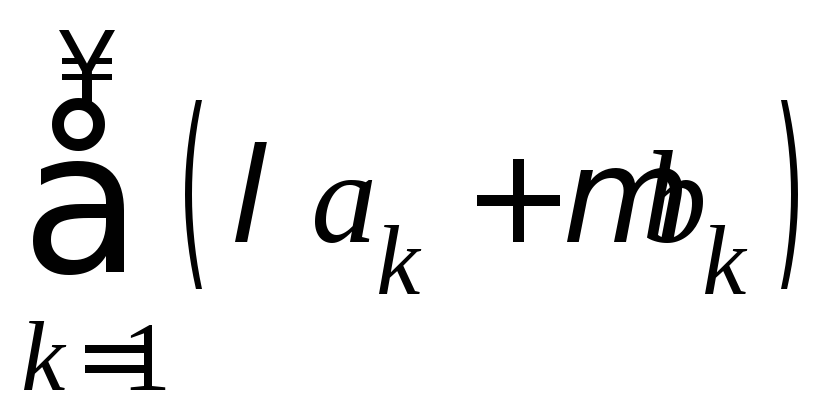1. (Линейность суммы ряда). Пусть даны сходящиеся рядыи. В таком случае при любыхрядтакже сходится и его сумма равна.

Доказательство.Так как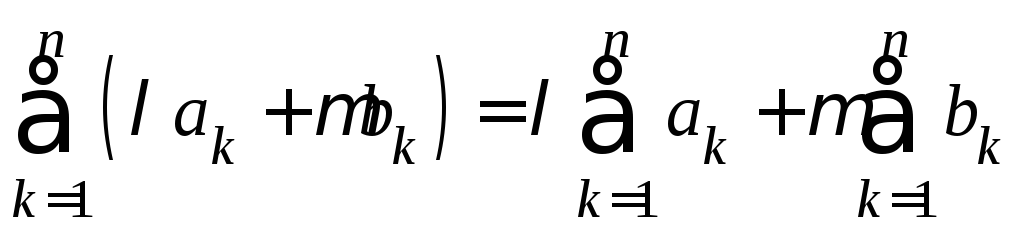, то остаётся лишь перейти в этом равенстве к пределу.

2. Если в сходящемся ряде ввести парные скобки, то сумма ряда не изменится. Отбрасывать скобки, вообще говоря, нельзя.

Доказательство. Частичные суммы рядаравны. Так как подпоследовательность сходящейся последовательности имеет тот же предел, что и у исходной последовательности, то суммы обоих рядов совпадают.

Контрпример. Рядсходится и его сумма равна нулю, а ряд без скобокрасходится, так как для него не выполнено необходимое условие сходимости.

3. Если произвести перестановку, затрагивающую конечное число членов ряда, то это не повлияет ни на сходимость, ни на сумму ряда. Это уже не верно для бесконечных перестановок членов ряда.

Доказательство. Пусть члены ряда с номерамипри перестановке не изменились. Тогда все частичные суммы рядас номерамитакже не изменились.

Контрпример. Рассмотрим ряд Лейбница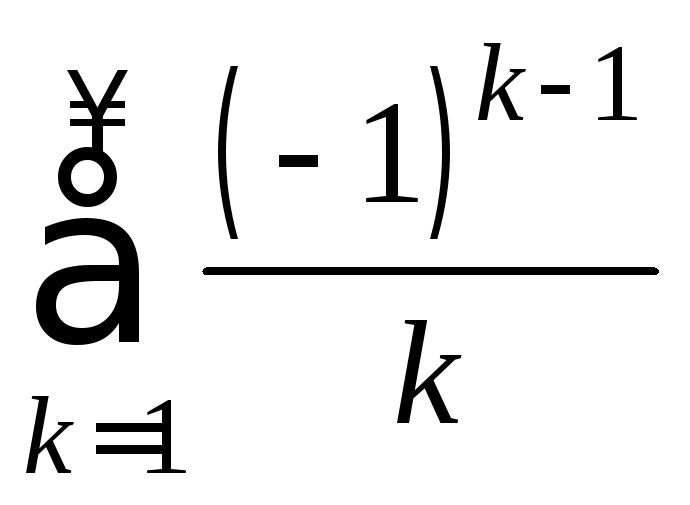. В одной из ближайших лекций будет доказано, что этот ряд сходится. Обозначимсумму этого ряда. Рассмотрим переставленный ряд. Легко доказать, что и этот ряд сходится. Сумма нового ряда равна

.

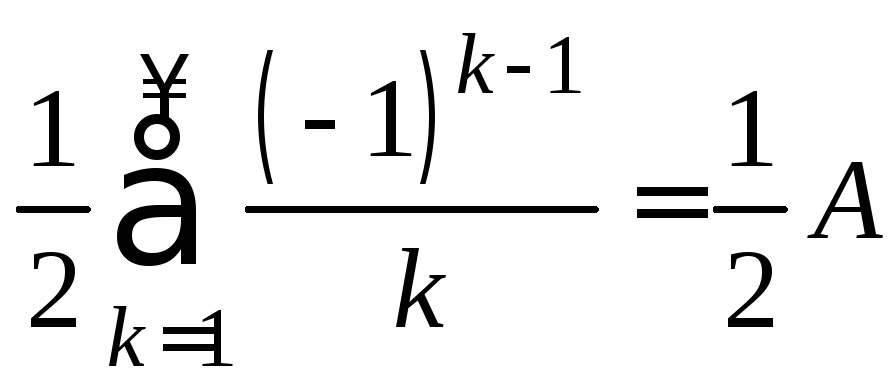Замечание. Ещё Лейбницу было известно, что.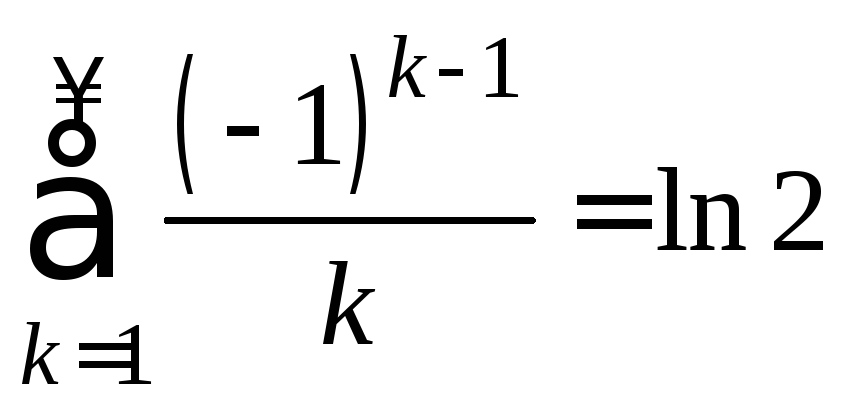

§2. Признаки сходимости рядов с неотрицательными членами.

1˚. Если все члены ряданеотрицательны, то последовательность его частичных сумм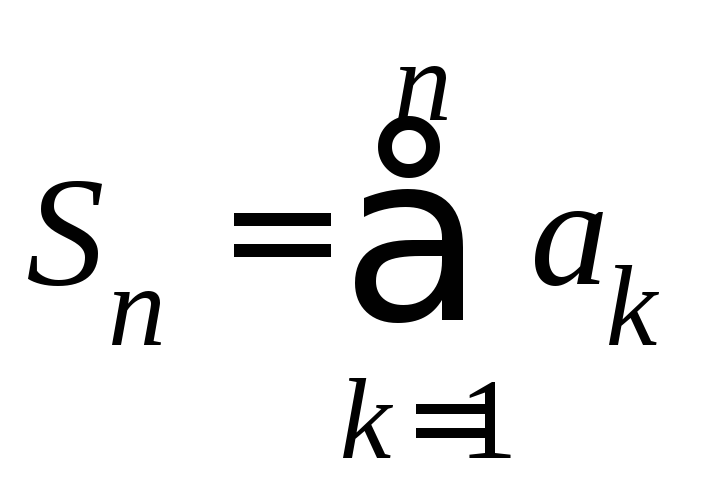неубывающая, следовательно, существует предел этой последовательности (конечный или бесконечный). Мы приходим к следующему выводу.

Предложение. Ряд с неотрицательными членами сходится тогда и только тогда, когда последовательность его частичных сумм ограничена.

2˚. Теорема (Интегральный признак Коши). Пусть неотрицательная функцияубывает на промежутке. Тогда ряд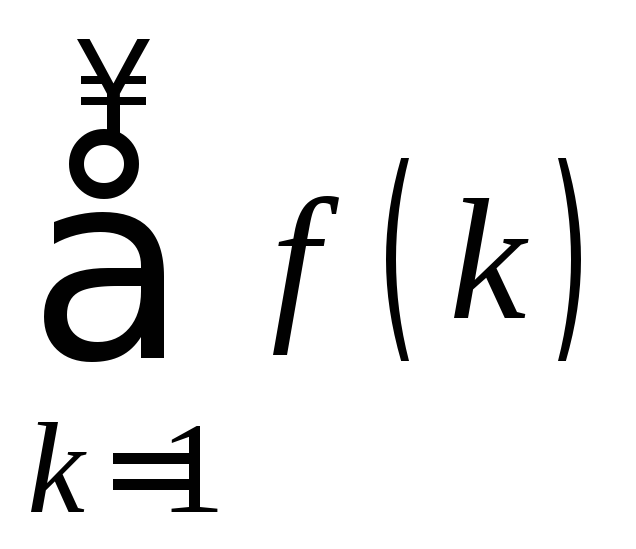и несобственный интегралоба сходятся, либо оба расходятся. В случае сходимости их остатки связаны неравенствами

.

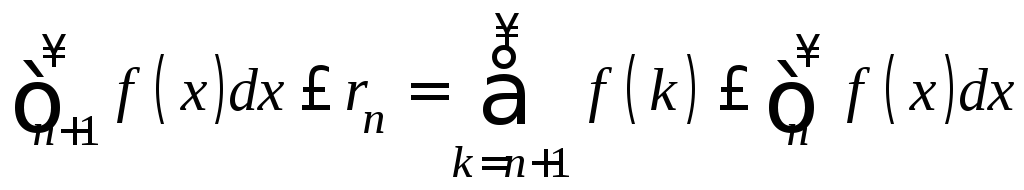Доказательство. Из условий теоремы следуют неравенства:

и,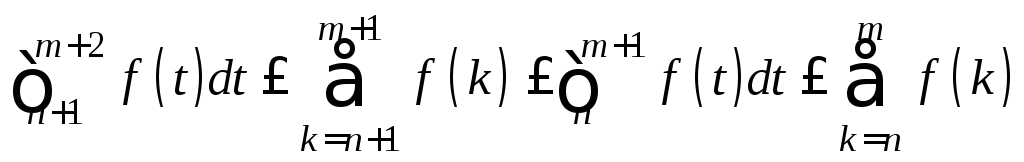

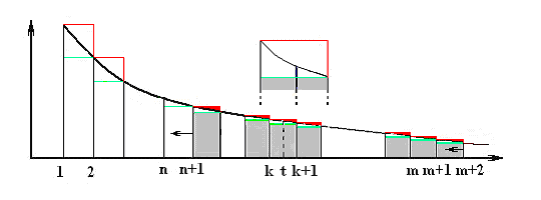
Пусть сначала известно, что сходится ряд и . Тогда

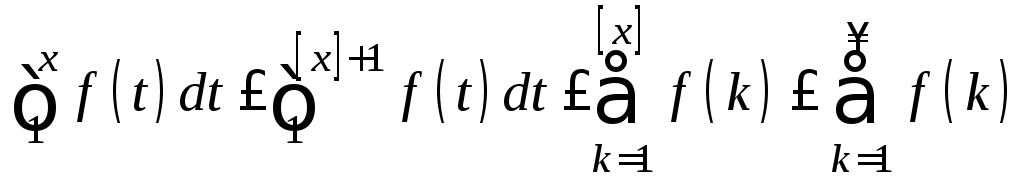, а так каквозрастает, то интегралсходится.

Наоборот, если сходится интеграл, то , следовательно, ряд сходится.

Наконец, оценку остатка получим из соотношения с помощью предельного перехода.

Следствие. Ряды Дирихлесходятсяи расходятся.

3˚. Теорема. (Признак сравнения). Рассмотрим ряды с положительными членам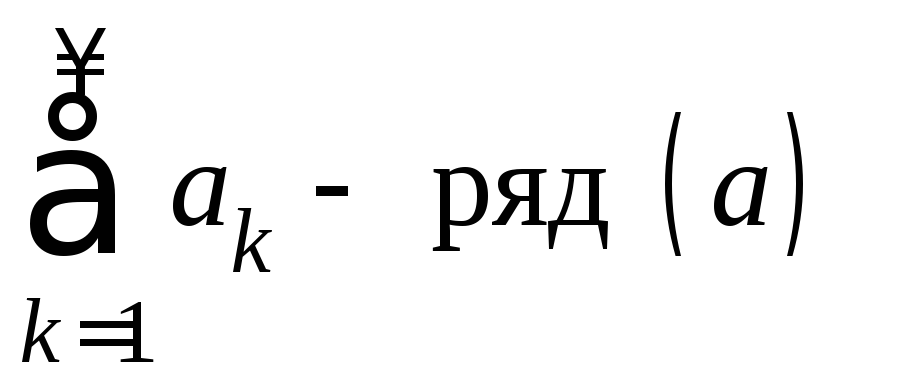и и.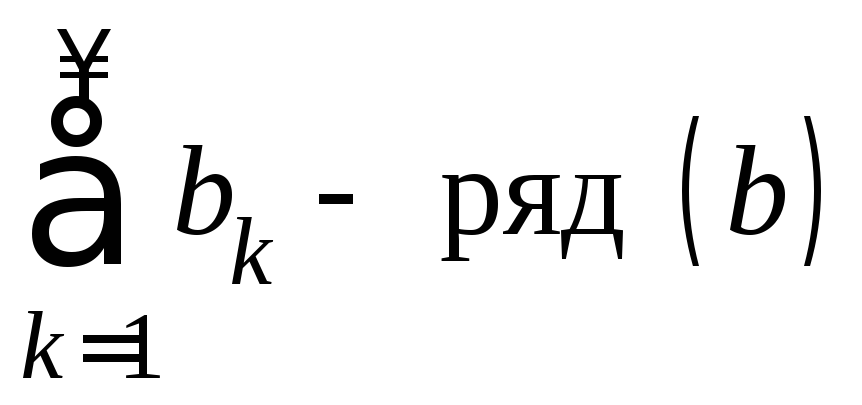

а) если ряд мажорируется рядом(т.е.) и рядсходится, то рядтакже сходится, при этом.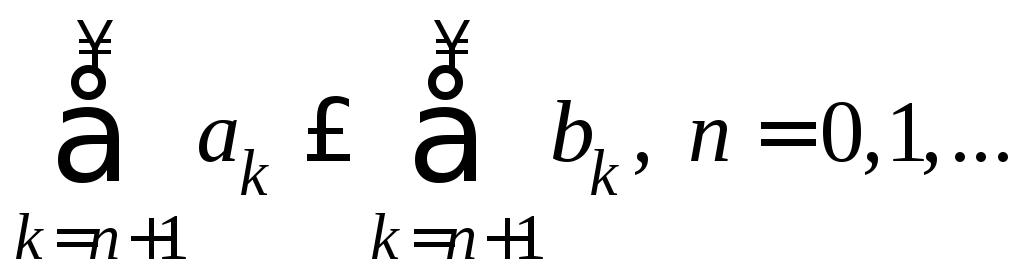

б) если 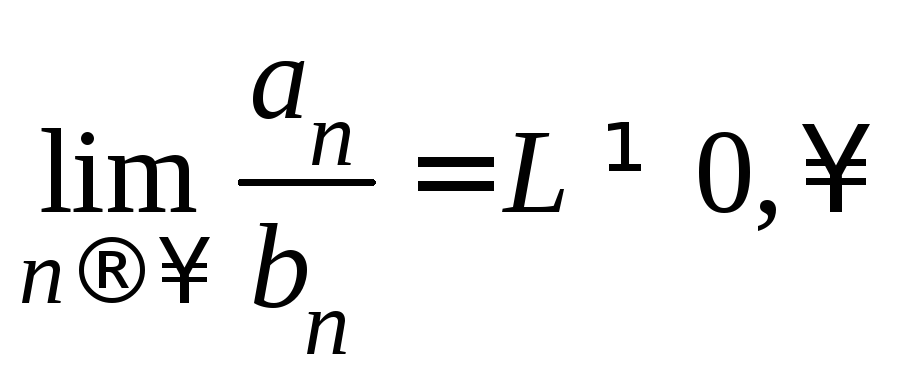, то рядыоба сходятся, либо оба расходятся.

Доказательство. Утверждение пункта а) сразу следует из неравенства.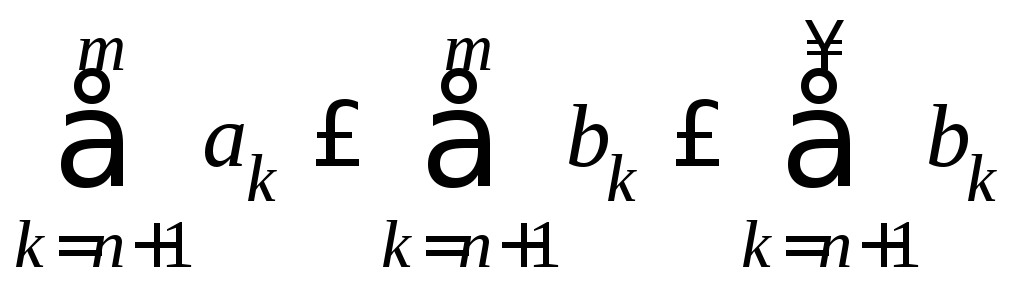

б) Так как 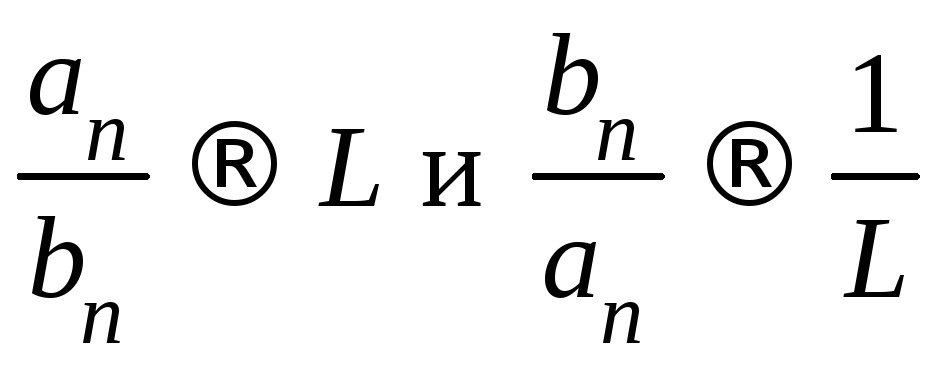, то оба эти отношения ограничены, т.е. существует положительное числотакое, чтои,. Остаётся воспользоваться утверждением пункта а).